Esercizio 1 - Matilde Consales

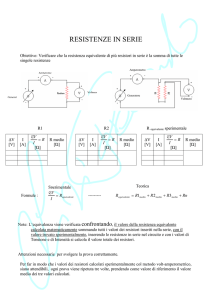
Esercizio 1
Dato lo schema di figura 1 determinare per quali valori del rapporto r/R esso è in grado di
convertire dati digitali in ingresso espressi in codice binario naturale e BCD.
Figura 1 Convertitore digitale analogico a resistori pesati.
Svolgimento
Lo schema rappresenta un convertitore digitale-analogico a resistori pesati. Il numero digitale da
convertire è di 8 bit. Per evitare l’uso di resistenze troppo elevate gli 8 resistori sono stati divisi in
due gruppi di 4 separati dalla resistenza r che, essendo percorsa dalla corrente Ir, varia il “peso”
delle resistenze alla sua sinistra (si crea, infatti, una caduta di tensione). Per risolvere l’esercizio
possiamo considerare solo i 4 bit più significativi. Con 4 bit si rappresentano 16 numeri in binario e
10 numeri in BCD (ricordiamo che con il codice BCD ciascuna cifra decimale è rappresentata da un
numero binario e che sono necessari 4 bit per rappresentare le cifre da 0 a 9).
Supponiamo ora di trovarci nella situazione rappresentata in figura 1 dove tutte le resistenze sono
collegate a massa eccetto R collegata a Vref. In questo caso R è l’unica resistenza percorsa da
corrente che vale:
𝑉𝑟𝑒𝑓
𝑅
Quando si converte un numero binario deve essere:
𝐼7 =
𝐼7
1 𝑉𝑟𝑒𝑓
=
16 16 𝑅
Quando, invece, si converte un numero BCD si deve avere:
𝐼𝑟 =
𝐼7
1 𝑉𝑟𝑒𝑓
=
10 10 𝑅
Dato che dobbiamo trovare il rapporto r/R è sufficiente calcolare la corrente Ir (vedi figura 1).
Conviene utilizzare il teorema di Norton1 ed effettuare il “taglio” a destra della resistenza r.
Disegniamo il circuito da considerare.
𝐼𝑟 =
1
Vedi http://cmathilde.altervista.org/Elettrotecnica/Norton.pdf
1
Figura 2 Il circuito in esame.
Troviamo la resistenza equivalente togliendo il “carico” (nel nostro caso la resistenza r) e
sostituendo un cortocircuito al generatore di tensione.
Figura 3 Lo schema per determinare la resistenza equivalente.
Dallo schema di figura 3 si vede che la resistenza equivalente è data dal parallelo dei quattro
resistori.
𝑅1 = 8𝑅||4𝑅 =
8𝑅 ∙ 4𝑅
32
8
=
𝑅= 𝑅
8𝑅 + 4𝑅 12
3
8
𝑅 ∙ 2𝑅
3
𝑅2 = 𝑅1 ||2𝑅 = 8
3
𝑅 + 2𝑅
16
=
𝑅𝑒𝑞 = 𝑅2 ||𝑅 = 8
7
𝑅+𝑅
=
3
8
𝑅∙𝑅
7
𝑅
3
14
8
=
𝑅
7
15
7
16
8
𝑅= 𝑅
14
7
=
8
𝑅
15
Adesso dobbiamo trovare la corrente di cortocircuito IN. Usiamo lo schema di figura 4.
Figura 4 Circuito per determinare la corrente di cortocircuito.
2
Abbiamo già calcolato il parallelo delle tre resistenze più a sinistra. Ridisegniamo il circuito.
Figura 5 Determinazione della corrente di cortocircuito.
La resistenza più a sinistra è cortocircuitata quindi la corrente cervata vale:
𝑉𝑟𝑒𝑓
𝑅
Possiamo trovare la corrente Ir. Consideriamo il circuito di figura 6.
𝐼𝑁 =
Figura 6 Schema per determinare Ir.
Applicando la formula del partitore di corrente si ricava:
8
𝐼𝑟 =
8
15
𝑅
𝑅+𝑟
15
𝐼𝑁
Sostituiamo a IN il valore determinato precedentemente:
8
𝐼𝑟 =
8
15
𝑅
𝑉𝑟𝑒𝑓
𝑅+𝑟 𝑅
15
Consideriamo il caso della conversione di un numero binario. Deve essere:
8
8
15
8
𝑅
15
8𝑅+15𝑟
15
=
1
16
→
𝑅
𝑉𝑟𝑒𝑓
1 𝑉𝑟𝑒𝑓
=
16 𝑅
𝑅+𝑟 𝑅
15
8𝑅
1
=
8𝑅 + 15𝑟 16
→
128𝑅 = 8𝑅 + 15𝑟
𝑟 = 8𝑅
3
→
120𝑅 = 15𝑟
Procedendo analogamente per la conversione di un numero BCD si trova:
8
8
15
8
𝑅
15
8𝑅+15𝑟
=
15
1
10
→
𝑅
𝑉𝑟𝑒𝑓
1 𝑉𝑟𝑒𝑓
=
10 𝑅
𝑅+𝑟 𝑅
15
8𝑅
1
=
8𝑅 + 15𝑟 10
→
80𝑅 = 8𝑅 + 15𝑟
𝑟 = 4.8𝑅
Questo file può essere scaricato gratuitamente. Se pubblicato citare la fonte.
Matilde Consales
4
→
72𝑅 = 15𝑟