Poligoni
inscritti e circoscritti
a una circonferenza
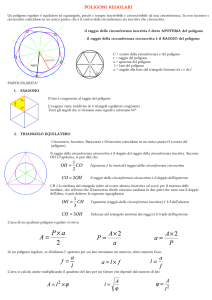
Definizioni
• Un poligono è inscritto in una
circonferenza se tutti i suoi vertici
appartengono ad essa.
• Un poligono è circoscritto a una
circonferenza se tutti i suoi lati sono
tangenti a essa.
Si possono inscrivere tutti i poligoni?
• No: soltanto i poligoni in cui esiste il circoncentro, cioè il punto di incontro degli assi
Esiste il circocentro
Note:
Asse di un lato
OB = raggio del poligono =
= raggio circonferenza
NON esiste il circocentro
Si possono circoscrivere tutti i poligoni?
• No: soltanto i poligoni in cui esiste l’incentro, cioè il punto di incontro delle bisettrici
Esiste l’incentro
P
Note:
Bisettrice di un angolo
OP = apotema = raggio
circonferenza.
L’apotema è la distanza di
ciascun lato dall’incentro.
NON esiste l’incentro
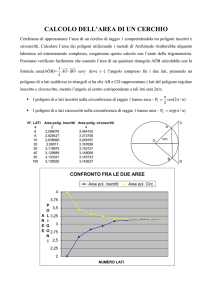
Triangoli inscritti e circoscritti:
Ogni triangolo ha sempre il circocentro e l’incentro
Note:
OP= raggio
OQ = apotema