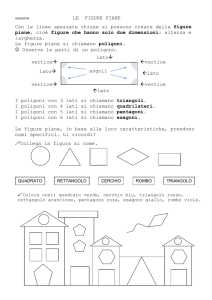
CALCOLO DELL’AREA DI UN CERCHIO
Cerchiamo di approssimare l’area di un cerchio di raggio 1 comprendendola tra poligoni inscritti e
circoscritti. Calcolare l’area dei poligoni utilizzando i metodi di Archimede risulterebbe alquanto
laborioso ed estremamente complesso, eseguiremo questo calcolo con l’aiuto della trigonometria.
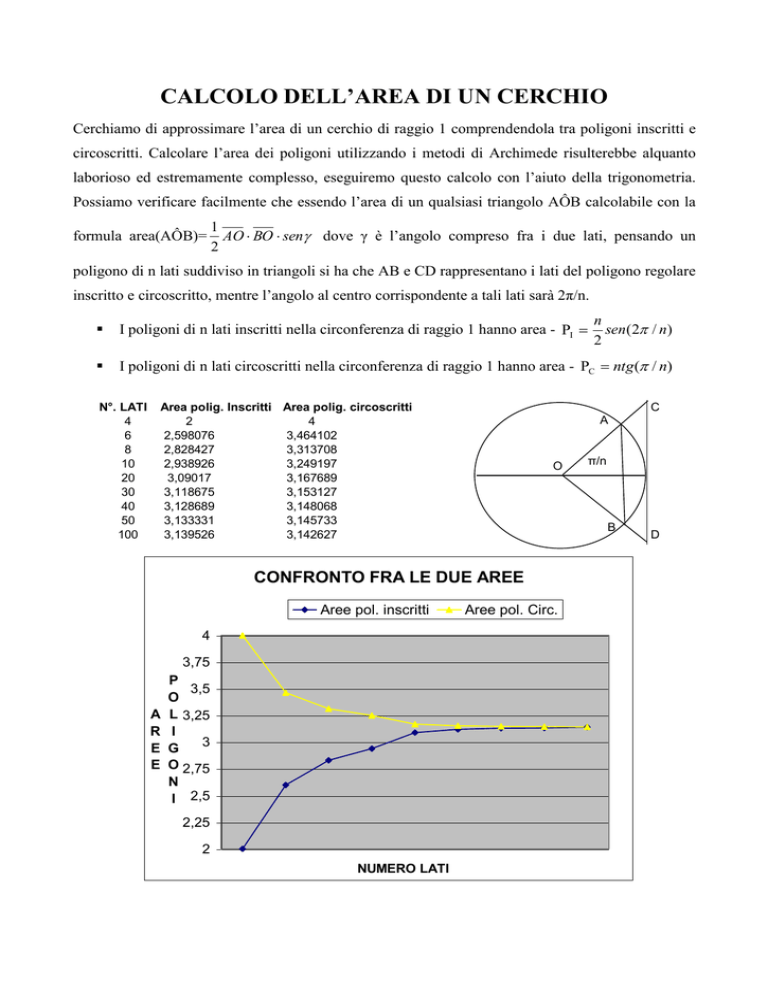
Possiamo verificare facilmente che essendo l’area di un qualsiasi triangolo AÔB calcolabile con la
formula area(AÔB)=
1
AO BO sen dove γ è l’angolo compreso fra i due lati, pensando un
2
poligono di n lati suddiviso in triangoli si ha che AB e CD rappresentano i lati del poligono regolare
inscritto e circoscritto, mentre l’angolo al centro corrispondente a tali lati sarà 2π/n.
n
sen ( 2 / n)
2
I poligoni di n lati inscritti nella circonferenza di raggio 1 hanno area - PI
I poligoni di n lati circoscritti nella circonferenza di raggio 1 hanno area - PC ntg ( / n)
N°. LATI
4
6
8
10
20
30
40
50
100
Area polig. Inscritti Area polig. circoscritti
2
4
2,598076
3,464102
2,828427
3,313708
2,938926
3,249197
3,09017
3,167689
3,118675
3,153127
3,128689
3,148068
3,133331
3,145733
3,139526
3,142627
C
A
O
B
CONFRONTO FRA LE DUE AREE
Aree pol. inscritti
4
3,75
A
R
E
E
P
3,5
O
L 3,25
I
3
G
O 2,75
N
I 2,5
2,25
2
NUMERO LATI
π/n
Aree pol. Circ.
D