ECONOMIA APPLICATA ALL’INGEGNERIA
ESERCIZI DI MICROECONOMIA
1. Disegnare il vincolo di bilancio di un consumatore che dispone della somma di denaro M=240
da spendere nell’acquisto di due beni, y1 e y2, i cui prezzi sono p1=24 e p2=48. Spiegare come
cambia il disegno quando il prezzo del secondo bene diventa p2’=96
Soluzione
L’equazione del vincolo di bilancio è
p1y1 + p2 y2 = M (in forma implicita)
y2 = M/p2 – (p1/p2)y1
Il grafico, con y1 in ascissa e y2 in ordinata, è una retta decrescente che
• incontra l’asse orizzontale nel punto M/p1 = 240/24 = 10
• incontra l’asse verticale nel punto M/p2 = 240/48 = 5
Il coefficiente angolare della retta, in valore assoluto, è il prezzo relativo p1/p2 = 1/2
Quando p2 aumenta diventando p2’ = 96 l’intercetta sull’asse verticale diminuisce, diventando
240/96 = 2.5 mentre quella sull’asse orizzontale rimane immutata: perciò la retta ruota verso il
basso (si vede anche che diminuisce il coefficiente angolare, che diventa p1/p2 = 24/96 = 1/4).
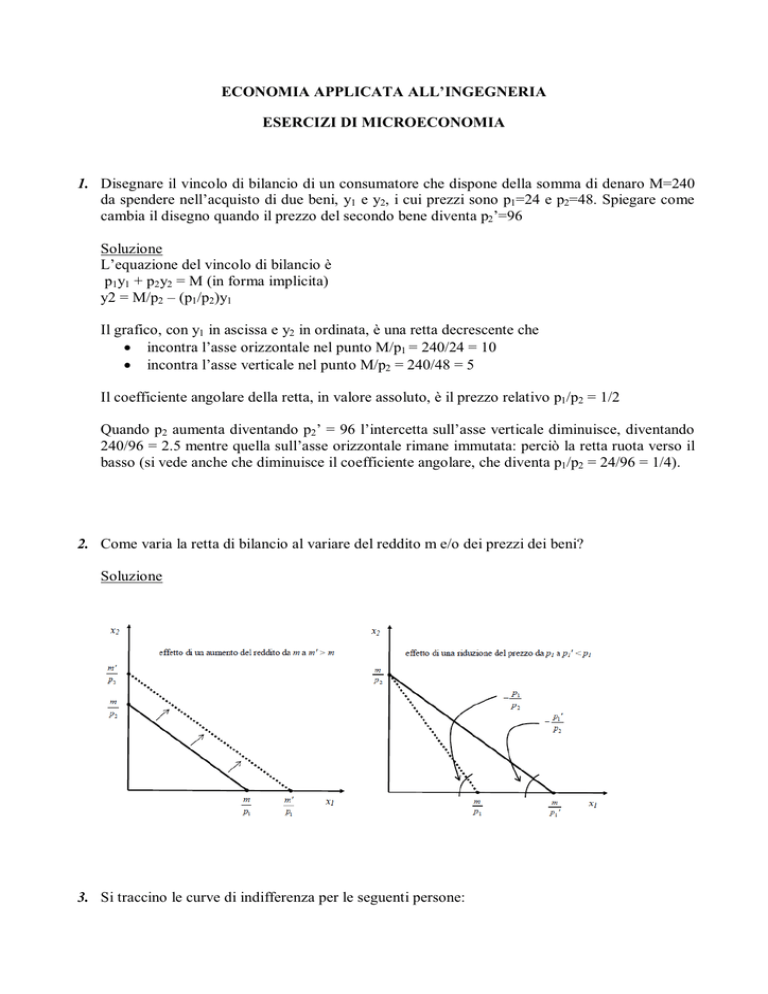
2. Come varia la retta di bilancio al variare del reddito m e/o dei prezzi dei beni?
Soluzione
3. Si traccino le curve di indifferenza per le seguenti persone:
a) John: «non ottengo nessuna soddisfazione da 1 etto di pasta o da 3 etti di carne ma
apprezzo moltissimo 1 etto di pasta e 3 etti di carne»
b) Mary: «non mi importa se la birra è una Pilsen o una Lager, purchè si tratti di birra»
c) Steve: «non sono disposto a tagliarmi i capelli per far piacere al mio capo, a meno che
questo non mi paghi; io richiedo 300 $ più 1$ per ogni centimetro di capelli tagliato»
d) Ann: «mi piacciono molto birra e salatini ma dopo 12 birre una birra in più mi fa sentire
male»
Soluzione
a) John vuole consumare un mix ben preciso di pasta e carne: questi due beni sono
perfettamente complementari. Le curve di indifferenza sono pertanto a forma di L
b) A Mary interessa solo bere birra e nient’altro: i due tipi di birra sono perfetti sostituti e le
curve di indifferenza devono avere inclinazione costante
c) La curva di indifferenza coincide con l’asse verticale fino a che non si raggiunge la somma
di 300$, dopo di che la curva di indifferenza diventa una linea retta con inclinazione pari a
1
d) La curva di indifferenza deve essere inclinata positivamente dopo la 12-esima birra: Ann
deve consumare più salatini per ogni ulteriore birra che beve dopo le prime 12
4. Le preferenze di Simona sono caratterizzate dal saggio marginale di sostituzione SMS=3y2/y1.
Quale è il significato economico del saggio marginale di sostituzione? Mostrare che, nel caso di
Simona, esso è decrescente. Sapendo che Simona ha a disposizione la somma M=240 e i prezzi
dei due beni sono p1=10 e p2=5, calcolare il paniere acquistato.
Soluzione
Il saggio marginale di sostituzione misura il numero di unità di y2 che il consumatore è disposto
a cedere in cambio di una unità in più di y1 restando indifferente tra il paniere di partenza e
quello di arrivo. Nel caso di Simona SMS è tanto più grande quanto maggiore è la disponibilità
iniziale di y2 e quanto minore è la disponibilità iniziale di y1 ; perciò esso diventa più piccolo
man mano che, lungo la curva di indifferenza, aumenta y1 e diminuisce y2.
Per calcolare la scelta di Simona si può procedere come segue.
SMS = p1/p2 3y2 = 2y1
10y1 + 5y2 = 240 (vincolo di bilancio).
Un semplice calcolo conduce al risultato y1 * = 18
y2 * = 12
5. La funzione di utilità di Corrado è U=y1∙y2. Calcolare il suo saggio marginale di sostituzione.
Corrado dispone della somma M=480 da spendere per i due beni. Sapendo che i loro prezzi
sono p1=12 e p2=4, calcolare i suoi acquisti. Successivamente cambiano i prezzi: quello del
primo bene si dimezza e quello del secondo si triplica. Come cambiano gli acquisti? Quale è la
situazione preferita da Corrado, la vecchia o la nuova?
Soluzione
SMS = Um1/Um2
Um1 = (y1 + 1) y2 − y1 y2 = y2
Um2 = (y2 + 1) y1 − y1 y2 = y1
SMS = y2/y1
p1=12 e p2=4 vincolo di bilancio: 12y1 + 4y2 = 480
dalla condizione SMS = p1/p2 si ricava facilmente y2 = 3y1
utilizzando questo risultato nel vincolo di bilancio si ottiene y1 = 20 e y2 = 60.
U = 60*20 = 1200
p1= 6 e p2=12 vincolo di bilancio: 6y1 + 12y2 = 480
dalla condizione SMS = p1/p2 si ricava facilmente y1 = 2y2
utilizzando questo risultato nel vincolo di bilancio si ottiene y1 = 40 e y2 = 20.
U = 20*40 = 800
L’utilità del paniere vecchio è maggiore, il che significa che il paniere vecchio si trova su una
curva di indifferenza più alta; in questo caso, il cambiamento dei prezzi ha ridotto il reddito
reale del consumatore.
6. La curva di domanda del bene A è ya=100-2pa; quella del bene B è yb=120−3pb. Calcolare le
quantità domandate per pa=pb=10 e quelle domandate quando due prezzi raddoppiano. Quale
delle due domande è più elastica?
Soluzione
ya (10) = 80
ya (20) = 60
yb (10) = 90
yb (20) = 60
Il calcolo delle elasticità dà
ξa = (20/80)/(10/10) = 1/4
ξb = (30/90)/(10/10) = 1/3 .
Le due domande sono entrambe “anelastiche”, ma quella del bene A è la più rigida delle due.
7. Il prezzo del bene y è p=50 e, a quel prezzo, la quantità domandata
è y=200. Sapendo che l’elasticità della domanda del bene è pari a 1.5,
calcolare la variazione della quantità domandata del bene se si verifica
un aumento del prezzo pari a 5
Soluzione
La definizione di elasticità della domanda è ξ = (Δy/y)/(Δp/p) in valore assoluto
Otteniamo subito Δp/p = 5/50 = 10%.
Perciò Δy/y = − ξ * Δp/p = − 1.5*10/100 = −15%.
Dato che il livello di partenza della quantità domandata era y = 200, si ha
Δy/200=−15/100 y = −30.
8. In una certa situazione produttiva, il saggio marginale di sostituzione tecnica tra capitale e
lavoro risulta uguale a 5 (si può sostituire una unità di capitale con 5 unità aggiuntive di
lavoro). D'altra parte, aumentando di 20 unità la quantità di lavoro impiegato - ferma restando
la quantità di capitale - la produzione aumenterebbe di 80000. Si calcoli il prodotto
(produttività) marginale del capitale.
Soluzione
Aumentando di 20 unità la quantità di lavoro impiegato, la produzione aumenta di 80000.
Perciò, aumentando di 5 unità la quantità di lavoro impiegato, la produzione aumenta
(all'incirca) di 80000/4=20000.
5 unità aggiuntive di lavoro equivalgono a 1 unità di capitale e l'incremento di produzione che
si può ottenere con una unità aggiuntiva di capitale (ossia il prodotto marginale del capitale) è
20000.
9. Nella figura è rappresentato l’isoquanto relativo alla produzione di 18.000 unità a settimana di
un certo prodotto secondo la tecnologia disponibile presso una data impresa. Si supponga
quindi che il prezzo dell'input "lavoro" sia 1000 e il prezzo dell'input "capitale" sia 0,4 e si
individui graficamente la combinazione dei due input che minimizza il costo di produzione di
quella quantità di prodotto.
Soluzione
Nella figura si traccia un qualunque isocosto, per esempio quello di livello 42000
1000 L + 0,4 K = 42000
Si traccia poi un isocosto parallelo al precedente e tangente all'isoquanto: il punto di tangenza P
corrisponde alla combinazione dei due input che minimizza il costo di produzione di quella
quantità di prodotto.
10. Si dispone dei seguenti dati: il prezzo dell’input variabile è w=10; il prezzo del prodotto è
p=40; la produttività marginale è Pm=8/y. Calcolare la quantità prodotta scelta dall’impresa.
Soluzione
La scelta dell’impresa (quella che massimizza il profitto) è identificata dalla condizione p=MC.
Il costo marginale à dato dalla formula MC = w/Pm = 5/4 * y
La condizione di massimo profitto è perciò 10 = 5/4 * y da cui y* = 8
11. Si consideri un mercato perfettamente concorrenziale in equilibrio di lungo periodo. L’offerta
del bene è fornita da un gran numero di imprese tutte identiche, il cui costo totale è Ct = 338 +
2y2 e il cui costo marginale è Cm = 4y. Calcolare il prezzo di equilibrio del mercato.
Soluzione
Quando un mercato è in equilibrio di lungo periodo i profitti sono nulli. Ciò si verifica quando
p = AC (costo medio).
Dato che la scelta dell’impresa è sempre identificata dalla condizione p = MC, segue che
devono valere entrambe le condizioni. Scriveremo perciò, uguagliando i secondi membri:
AC = MC.
AC = Ct/y = 338/y +2y y = 13
Il prezzo di equilibrio di lungo periodo del mercato risulta essere pari a p=4*13=52.
12. Nel mercato, perfettamente concorrenziale, di un certo prodotto, la domanda è rappresentabile
con la seguente espressione: p=100-30Q. In una situazione di equilibrio di lungo periodo del
mercato, il prezzo è 10 e la quantità venduta è 3. Si supponga che, in conseguenza di
cambiamenti intervenuti su altri mercati, la domanda si modifichi come segue: p=110-30Q.
Nell'ipotesi che l'industria considerata sia caratterizzata da costi costanti, si determinino il
nuovo prezzo e la nuova quantità di equilibrio di lungo periodo, descrivendo brevemente i
successivi cambiamenti che portano dalla vecchia alla nuova situazione di equilibrio a seguito
del cambiamento della domanda.
Soluzione
Se la situazione iniziale è un equilibrio di lungo periodo del mercato, ciò significa che il prezzo
corrisponde al costo medio minimo. Dunque il costo medio minimo di lungo periodo è pari a
10.
Se la domanda aumenta, inizialmente il prezzo crescerà al di sopra del costo medio, creando
extraprofitti che attireranno altre imprese nel mercato. La nuova offerta aggiuntiva farà
scendere il prezzo fino a raggiungere di nuovo il livello minimo di 10.
Nella nuova situazione di equilibrio di lungo periodo il prezzo sarà di nuovo 10; la quantità
scambiata, deducibile dalla nuova funzione di domanda, sarà Q = (110 - 10)/30 = 10/3.
13. Un bene è venduto in un mercato di concorrenza perfetta al prezzo di 100, in condizioni di
equilibrio di lungo periodo del mercato. La quantità venduta è di 10000 pezzi alla settimana.
L'elasticità della domanda è stimata in -2,5. Quali effetti avrà su prezzo e quantità venduta, nel
lungo periodo, un aumento del 2% nel costo di produzione?
Soluzione
Poiché sia la situazione iniziale che quella finale sono di equilibrio di lungo periodo in un
mercato di concorrenza perfetta, il prezzo in entrambi i casi sarà uguale al costo. Pertanto il
prezzo aumenterà del 2% (passando da 100 a 102) e la quantità venduta diminuirà del 5%
(ottenuto come prodotto dell'elasticità per la variazione percentuale del prezzo) e passerà quindi
da 10000 a 9500.
14. L’impresa Argentina opera in un mercato perfettamente concorrenziale. La sua funzione di
produzione è y=√x. Il prezzo di mercato è p=80 e il salario è w=10. Conosciamo il livello del
suo costo totale, che è Ct=400 e conosciamo anche il suo costo fisso, che è Cf=150. Calcolare la
quantità prodotta e il profitto conseguito dall’impresa. Supponendo che tutte le imprese siano
identiche ad Argentina, dire se il mercato si trova in equilibrio di breve o di lungo periodo.
Soluzione
Ct = k+wx
400=150+10x
x=250/10=25
y=√25=5
π=R -C
t
t
Rt = p(y)=80(5)=400