TEOREMA DI GAUSS
Si consideri una superficie chiusa con n cariche all’interno. Il flusso uscente da questa superficie
chiusa è uguale a:
∑
Φ =
In cui ∑ rappresenta la somma delle cariche racchiuse entro la superficie.
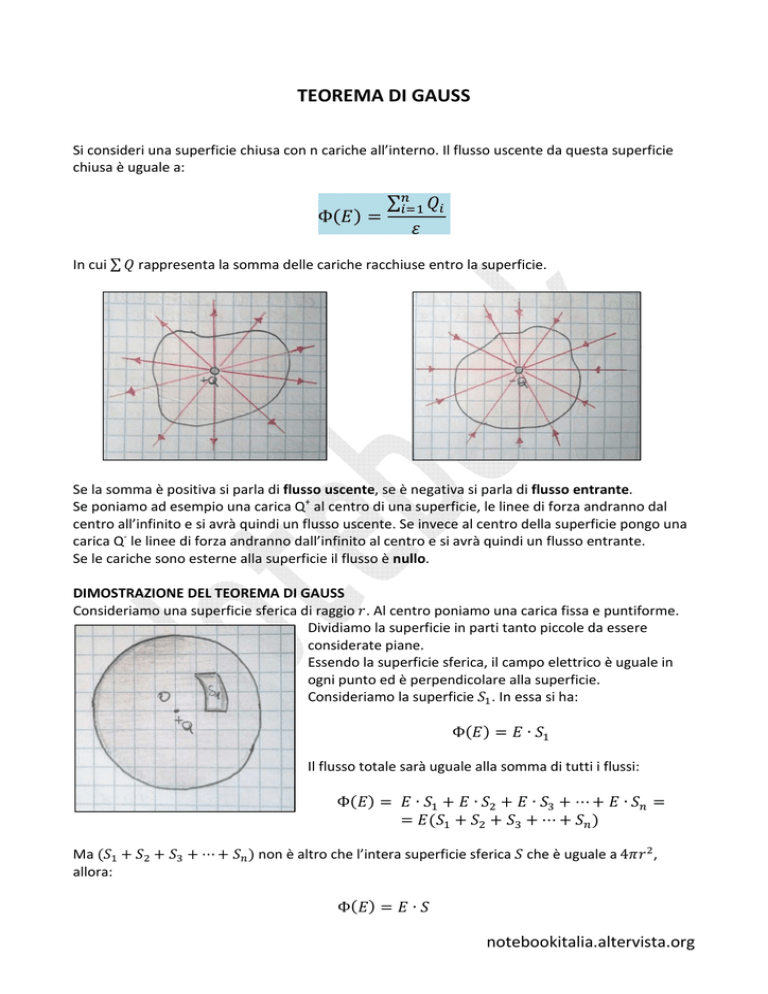
Se la somma è positiva si parla di flusso uscente, se è negativa si parla di flusso entrante.
Se poniamo ad esempio una carica Q+ al centro di una superficie, le linee di forza andranno dal
centro all’infinito e si avrà quindi un flusso uscente. Se invece al centro della superficie pongo una
carica Q- le linee di forza andranno dall’infinito al centro e si avrà quindi un flusso entrante.
Se le cariche sono esterne alla superficie il flusso è nullo.
DIMOSTRAZIONE DEL TEOREMA DI GAUSS
Consideriamo una superficie sferica di raggio . Al centro poniamo una carica fissa e puntiforme.
Dividiamo la superficie in parti tanto piccole da essere
considerate piane.
Essendo la superficie sferica, il campo elettrico è uguale in
ogni punto ed è perpendicolare alla superficie.
Consideriamo la superficie . In essa si ha:
Φ = ∙ Il flusso totale sarà uguale alla somma di tutti i flussi:
Φ = ∙ + ∙ + ∙ + ⋯ + ∙ =
= + + + ⋯ + Ma + + + ⋯ + non è altro che l’intera superficie sferica che è uguale a 4 ,
allora:
Φ = ∙ notebookitalia.altervista.org
Essendo = ⁄ e = 1⁄4 , allora:
Φ =
1 ∙ ∙ 4 =
4 È così dimostrato il teorema di Gauss secondo il quale in una superficie chiusa con cariche (nella
dimostrazione abbiamo considerato una sola carica Q+) il flusso è dato dalla somma delle cariche
diviso ε.
notebookitalia.altervista.org












