La trasformata di Laplace

Elettronica e Telecomunicazioni
Classe Quinta
La trasformata di Laplace
ELETTRONICA E TELECOMUNICAZIONI
CLASSE QUINTA A INFORMATICA
INDICE
•
•
•
•
•
•
•
Segnali canonici
Trasformata di Laplace
Teoremi sulla trasformata di Laplace
Funzione di Trasferimento
Anti-trasformata di Laplace
Esempio del circuito RC
Disegno del grafico nel dominio del tempo del
segnale
Segnali canonici
I segnali canonici sono utili per analizzare il comportamento di un sistema lineare.
Potremmo definirli come i segnali di uso più comune per valutare la risposta del sistema.
Ecco alcuni dei segnali canonici più usati:
Segnali canonici
Segnali canonici
Segnali canonici
Segnali canonici
Segnali canonici
Trasformata di Laplace
Si constata che data una rete elettrica, noto il
segnale d’ingresso e(t), per ottenere l’uscita u(t),
bisogna risolvere una equazione differenziale che è
in genere di non facile soluzione.
La trasformata di Laplace è un operatore
matematico che consente di semplificare lo studio
di un sistema.
Questo studio avviene nel dominio complesso;
successivamente si torna nel dominio del tempo
attraverso l’operatore inverso: antitrasformata di
Laplace.
Applicando la trasformata di Laplace ad un sistema, a prima vista
sembra di allungare il procedimento per la risoluzione dell’uscita.
In effetti occorre trasformare ogni elemento del circuito iniziale ed
ogni segnale applicato nel suo equivalente con Laplace.
Vantaggi della Trasformata di Laplace
I principali vantaggi che si ottengono con l’introduzione
della T.d.L. sono:
• Le equazioni differenziali sono tramutate in equazioni
algebriche;
• Nota l’uscita nel dominio di s U(s) anti-trasformando si
può risalire alla u(t);
• il sistema può essere rappresentato mediante la sua
funzione di trasferimento (F.d.T.);
La trasformata di Laplace dei segnali canonici
• Gradino unitario:
u(t)  1 / s
• Impulso unitario (delta di Dirac)
(t)  1
La trasformata di Laplace dei segnali canonici
• Rampa unitaria:
r(t)  1 / s2
• Parabola unitaria
p(t)  1 / s3
• Segnale sinusoidale
𝝎
 𝟐 𝟐
𝒔 +𝝎
s(t)
• Segnale cosinusoidale
s(t)
𝒔
𝟐 𝟐
𝒔 +𝝎
Teoremi sulle trasformate di Laplace
Teoremi sulle trasformate di Laplace
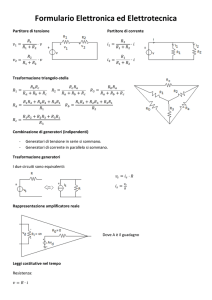
La trasformata di Laplace per la
resistenza, l’induttanza e la capacità
Nel caso in cui il condensatore e/o l’induttore siano inizialmente scarichi:
La trasformata di Laplace per la
resistenza, l’induttanza e la capacità
Nel caso invece in cui il condensatore e/o l’induttore siano inizialmente
carichi ad un valore Vc(0) per il condensatore e iL(0) per l’induttore:
Un esempio: il circuito RC
Determinare la tensione di uscita ai capi del condensatore C:
Passo 1: si trasforma il circuito, i suoi elementi ed i segnali ad esso applicati
Laplace
I(s)
Vi(s)
1/sC
Vc(s)
Il circuito trasformato adesso è lineare e per esso vale la legge di Ohm.
Passo 2: si ricava la corrente I(s)
Passo 3: si ricava la tensione di uscita Vout(s)
Passo 4: definiamo una nuova grandezza data dal rapporto fra Vout(s) e Vi(s)
La funzione di trasferimento
La F(s) determinata appena adesso prende il
nome di FUNZIONE DI TRASFERIMENTO (F.d.T)
del circuito.
Essa è il rapporto tra la L-Trasformata della
risposta di un sistema e la L-Trasformata della
corrispondente sollecitazione d'ingresso.
G(s)
=
Poli e zeri della F.d.T
Prendono il nome di ZERI gli n valori finiti di s che
annullano il Numeratore della F.d.T.
Prendono il nome di POLI gli m valori finiti di s che
annullano il Denominatore della F.d.T.
La F.d.T. è sempre data dal rapporto di due polinomi:
Se chiamiamo z1,… zn gli n ZERI e p1,…, pm gli m POLI, la F.d.T. si potrà scrivere come:
ANTITRASFORMATA DI LAPLACE
ESEMPI DI ANTITRASFORMATA
c
Antitrasformata di Laplace
(esempio del circuito RC visto prima)
Da quanto visto prima, al punto 3 dell’esercizio precedente, avevamo trovato che:
Da cui:
=
1
𝑅𝐶
𝑠+
1
𝑅𝐶
∙ 𝑉𝑖𝑛 (𝑠)
Passo 5: Utilizzando la formula di antitrasformazione:
dove a = 1/RC e K=1/RC, si ottiene:
𝑽𝒐𝒖𝒕 𝒕 = 𝑲 ∙
𝒆−𝒂𝒕
𝑲
𝒔+𝒂
→ 𝒌 ∙ 𝒆−𝒂𝒕
𝟏
𝟏
− 𝑹𝑪 ∙ 𝒕
=
∙ 𝒆
𝑹𝑪
Disegno del grafico della tensione di
uscita Vout(t)
Passo 6: si determinano i limiti della Vout(t) per t  0 e per t  
Per t  0
Per t  
𝑉𝑜𝑢𝑡 0 =
𝑉𝑜𝑢𝑡  =
𝟏
𝑹𝑪
𝟏
𝑹𝑪
∙ 𝒆
−
∙ 𝒆
𝟏
∙𝟎
𝑹𝑪
−
=
𝟏
𝑹𝑪
=
𝟏
∙
𝑹𝑪
𝟏 1
=0
𝑹𝑪 𝑒 
Vout(t)
Passo 7: si disegna il grafico
1/RC
Curva esponenziale descrescente
t