esercizio

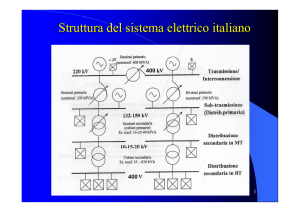
ESERCIZIO
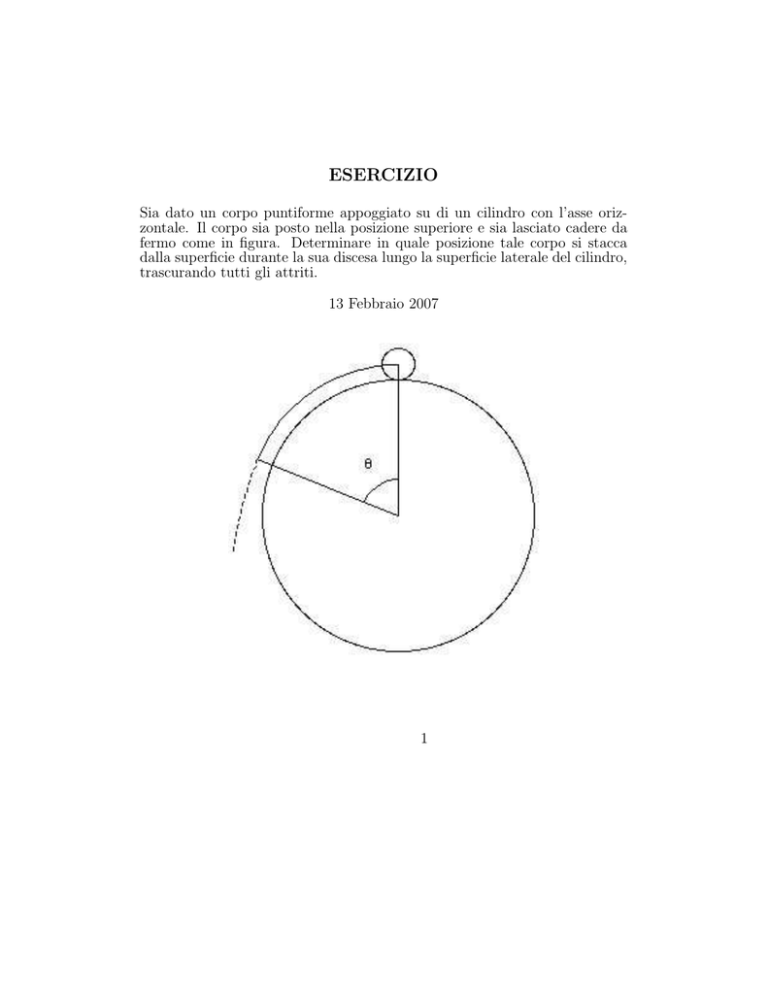
Sia dato un corpo puntiforme appoggiato su di un cilindro con l’asse orizzontale. Il corpo sia posto nella posizione superiore e sia lasciato cadere da
fermo come in figura. Determinare in quale posizione tale corpo si stacca
dalla superficie durante la sua discesa lungo la superficie laterale del cilindro,
trascurando tutti gli attriti.
13 Febbraio 2007
1
SOLUZIONE
Il corpo cade da fermo, e quindi l’energia potenziale che perde viene trasformata in energia cinetica. La legge di conservazione dell’energia ci fa scrivere
1 2
mv = mgh
2
(1)
h = R − Rcosθ = R(1 − cosθ)
(2)
dove h può essere scritto
Quindi mano a mano che il corpo scende acquista velocità e perde energia
cinetica, sotto la spinta della forza peso. Nel sistema di riferimento inerziale
del laboratorio, le forze che agiscono sul corpo sono:
• forza peso P - che si scompone con una componente tangenziale che
serve a trascinare il corpo verso il basso ed una componente radiale.
• reazione vincolare di appoggio sulla superficie del cilindro Rv - parallela
alla componente radiale della forza peso.
Inoltre, dal momento che il corpo compie un moto circolare, la risultante delle
forze applicate dovrà necessariamente svolgere il ruolo della forza centripeta
Fcp , diretta verso il centro della circonferenza su cui scorre il corpo ed ha
modulo uguale a mv 2 /r. Da notare che il modulo della forza centripeta non
è costante dal momento che il corpo scendendo aumenta la propria velocità.
La forza peso rimane costante durante tutto il moto, ma le sue componenti
(radiale PR e tangenziale PT alla traiettoria) e le altre forze variano a seconda della posizione assunta dal corpo durante la discesa. All’inizio la forza
2
centripeta necessaria a tenere il corpo in un moto circolare uniforme è minore
della componente radiale della forza peso e pertanto il corpo rimane attaccato
alla superficie; man mano che il corpo scende la componente radiale della
forza peso diminuisce il suo modulo, mentre la forza centripeta necessaria
a tenere il corpo attaccato al cilindro aumenta. Prima del distacco dalla
superficie sul corpo, la componente radiale della forza peso è maggiore della
forza centripeta per tenere il corpo attaccato alla traiettoria circolare (la cui
differenza è compensata dalla presenza della reazione vincolare), mentre la
componente tangenziale fa accelerare il corpo. Lungo la direzione radiale,
P~R + R~v = F~cp
(3)
dove Fcp è la forza centripeta che tiene il corpo attaccato ad un moto circolare.
Esiste una posizione in cui la forza centripeta e la componente radiale della
forza peso sono uguali (la reazione vincolare è nulla). Da questa posizione
in poi, la componente radiale della forza peso non riesce piu’ ad avere un
modulo tale da agire da forza centripeta e quindi il corpo si stacca dalla
superficie. In pratica la posizione limite è quindi definita dall’uguaglianza
della componente radiale della forza peso con la forza centripeta
P cosθ = m
v2
R
(4)
dove mv 2 può essere sostituito con quanto ricavabile dall’eq. 1. Questo porta
a
1
P cosθ = mgcosθ = 2mgR(1 − cosθ) = 2mg(1 − cosθ)
(5)
R
da cui si ottiene
cosθ = 2(1 − cosθ)
(6)
3
Questo risultato mette in evidenza che non c’è alcuna dipendenza dalla massa
del corpo e dal raggio del cilindro. La soluzione dell’eq. 6 è data dalla
soluzione della seguente equazione
cosθ =
2
3
(7)
che vale quindi θ = 0.841 radianti, circa 48 gradi.
Possiamo anche risolvere il presente esercizio in un sistema di riferimento non
inerziale solidale con il corpo. In tale situazione, lungo la direzione radiale
sul corpo agiscono le seguenti forze:
• forza peso - componente radiale.
• reazione vincolare di appoggio sulla superficie del cilindro - parallela
alla componente radiale della forza peso.
• forza centrifuga - uguale e contraria alla forza centripeta.
In questo caso, l’equilibrio lungo la direzione radiale è dato da
da cui si ha
P~R + R~v + F~cf = 0
(8)
P~R = −(R~v + F~cf )
(9)
e la posizione limite è data dall’uguaglianza del modulo della componente
radiale della forza peso con quello della forza centrifuga (reazione vincolare
di appoggio uguale a 0). Questa condizione porta a scrivere l’eq. 4, la cui
soluzione è identica al caso sviluppato nel sistema di riferimento inerziale.
Da notare che le due trattazioni relative al sistema di riferimento inerziale
del laboratorio e del sistema di riferimento non inerziale solidale col corpo,
sono assolutamente equivalenti; infatti l’eq. 3 può essere riscritta
P~R + R~v − F~cp = P~R + R~v + F~cf = 0
da cui segue l’eq. 9.
4
(10)