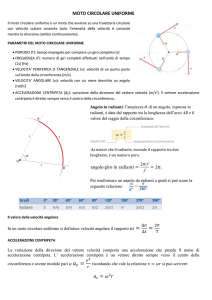
MOTO CIRCOLARE UNIFORME
Allora: la prof. ha fatto una spiegazione tremendamente disordinata del moto circolare.
Innanzitutto, il primo punto che non è ben chiaro
IL MOTO CIRCOLARE NON GENERA UNA FORZA CENTRIPETA, ma è il contrario: il
moto circolare implica una forza centripeta esterna.
Al massimo il moto circolare genera una forza centrifuga come reazione alla forza centripeta
che viene applicata.
Faccio un esempio: immaginate un corpo che si muove in moto rettilineo uniforme nello spazio. Se
io lo tiro verso di me con forza costante ma direzione variabile in base alla posizione (ovvero, lo
tiro sempre verso di me, dovunque si trovi) il suo moto diventa rotatorio circolare uniforme attorno
a me. Sono io che applico una forza centripeta al corpo mentre ne subisco la reazione centrifuga. (Il
corpo non esercita una forza centripeta su di me).
Chiarito questo punto si può passare al secondo “mistero” della lezione di oggi. Nell'esempio del
tappo che gira appeso a un filo, la prof. ha detto che la forza centripeta è la tensione del filo. In quel
caso, se non ci fosse stato un filo teso, il corpo se ne sarebbe andato per i fatti suoi in linea retta. A
generare il moto rotatorio era proprio la tensione (centripeta!) del filo causata dalla massa appesa
sotto. Infatti se non c'era la massa sotto, alla prima spinta il tappo se ne andava.
Se vogliamo vedere tutto al contrario, il moto rotatorio GENERA una forza centrifuga (come
ipotizzava Abbo) che va a contrastare il peso della massa sotto.
Detto questo, passiamo alla parte facile, solo di ripasso.
T = perido= tempo impiegato a percorrere un giro completo
f = frequenza = numero di giri in un secondo = 1/T
v = modulo della velocità tangenziale
ω = velocità angolare
[s] secondi
[H] Hertz = 1/s
[m/s] metri al secondo
[rad/s] radianti al secondo,
[°/s] gradi al secondo o [H]
(per chi non sa la fisica)
formule:
v = 2πr / T = 2πrf
ω = Δα / Δt
ω = 2π (rad) / T
Un radiante è un angolo che che stacca su qualunque circonferenza un arco lungo come il raggio.
Corrisponde a
360° / 2π = circa 57,29°
v = ωr
Fcentripeta = mωv = m v2 / r
Acentripeta = ωv