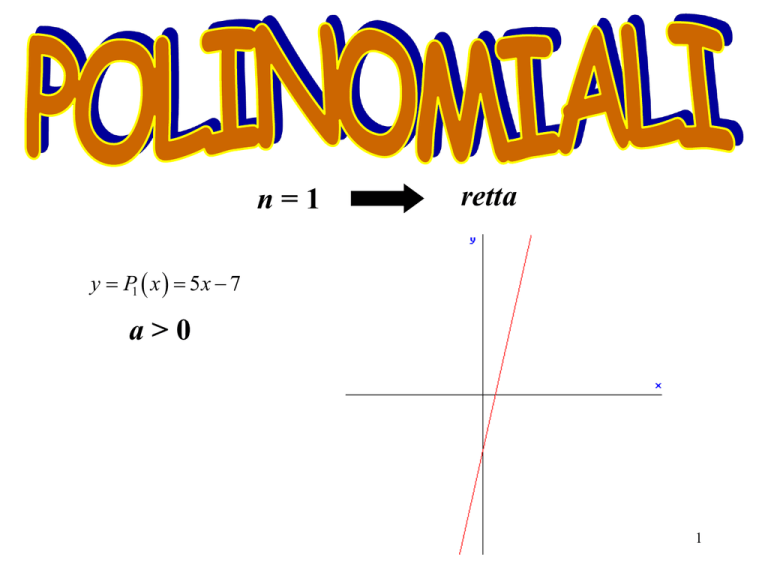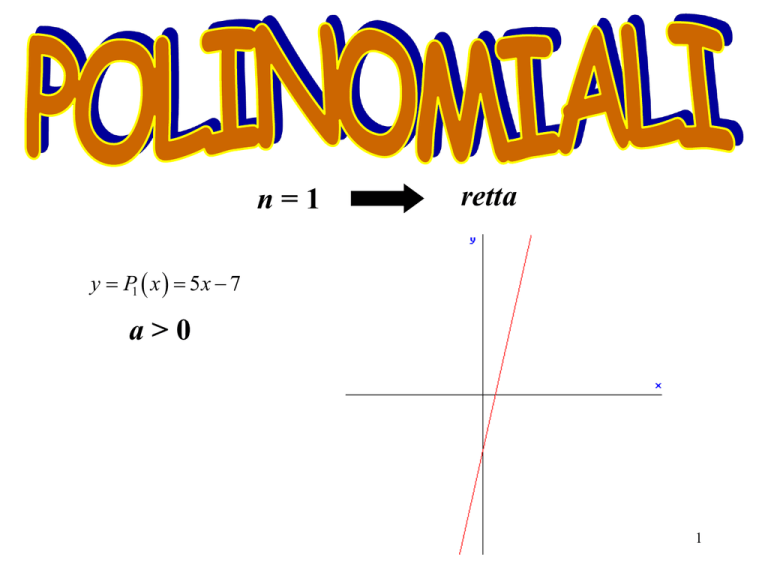
n=1
retta
y P1 x 5 x 7
a>0
1
n=1
retta
y P1 x 3x 2
a<0
2
n=2
parabola
y P2 x 2 x 2 5 x 1
a>0
concavità verso l’alto
3
n=2
parabola
y P2 x x 2 3x 8
a<0
concavità verso il basso
4
n=3
cubica
y P3 x 5 x3 x 2 3
a>0
5
n=3
cubica
y P3 x x3 2 x 2 x 2
a<0
6
Esempio 1
y P2 x x 2 7 x 5
n=2
1) Determinazione del campo di esistenza (C.E.)
C.E. = R = xR : < x < +
Ogni polinomio, indipendentemente dal grado,
è definito su tutta la retta reale, cioè su tutto R
C.E. = R = xR : < x < +
7
y P2 x x 2 7 x 5
2) Studio del segno della funzione
y 0 x2 7 x 5 0
cambiando il segno ed il
verso della disequazione
y 0 x2 7 x 5 0
trovando le soluzioni
dell’equazione associata
7 49 20 7 69
x 7 x 5 0 x1,2
2
2
2
8
7 69
7 69
x 7x 5 0
x
2
2
2
y 0 x2 7 x 5 0 x2 7 x 5 0
7 69
2
7 69
7 69
x
2
2
7 69
2
------- +++++ ------y<0
y>0
y<0
9
y P2 x x 2 7 x 5
3) Intersezioni con gli assi
x 0
2
y x 7x 5
intersezione con l’asse y,
ovvero con la retta x = 0
y 0
2
0 x 7 x 5
intersezione con l’asse x,
ovvero con la retta y = 0
10
y P2 x x 2 7 x 5
x 0
x 0
A 0,5
2
y 5
y x 7x 5
intersezione con l’asse y
y 0
y 0
2
7 69
x
7
x
5
0
x
1,2
2
7 69
,0
B
2
7 69
,0
C
2
intersezioni con l’asse x
11
y P2 x x 2 7 x 5
4) Limiti agli estremi del C.E.
C.E. = R = xR : < x < +
2
lim y lim x 7 x 5 ???
x
x
2
lim y lim x 7 x 5 ???
x
x
12
In generale:
n
n 1
n2
n
n
lim a0 x a1 x a2 x ... an lim a0 x a0 lim x
x
x
x
se a0 è positivo, n
se a0 è negativo, n
n
n 1
n2
n
n
lim a0 x a1 x a2 x ... an lim a0 x a0 lim x
x
x
x
se n è pari ed a0 è positivo
se n è pari ed a0 è negativo
se n è dispari ed a0 è positivo
se n è dispari ed a0 è negativo
13
y P2 x x 2 7 x 5
2
2
2
lim y lim x 7 x 5 lim x lim x
2
x
x
x
lim y lim x 7 x 5 lim x
2
x
x
x
x
2
lim x
2
x
2
la funzione data non ammette asintoti orizzontali
x+y
xy
14
y P2 x x 2 7 x 5
5) Calcolo della derivata prima
D( x n ) nx n1
D(a0 x n ) a0 D x n a0 nx n1
D(a0 ) 0
D( x) 1
D P1 x P2 x ... Pn x D P1 x D P2 x ... D Pn x
y ' D P2 x D x 2 7 x 5 D x 2 D 7 x D 5
2 x 7 0 2 x 7
15
y P2 x x 2 7 x 5
6) Studio del segno della derivata prima
y ' 0 2 x 7 0 2 x 7 2 x 7 x
7
2
7
2
+++++ ------y > 0
y < 0
M
16
y P2 x x 2 7 x 5
x
7
2
è un massimo per la funzione
2
7
69
7
7
7
x
y P2 7 5
2
4
2
2
2
7 69
M ,
2 4
è un punto di Massimo per la funzione
17
y P2 x x 2 7 x 5
7) Grafico della funzione
y
M
A
B
C
x
18
Esempio 2
n=3
y P3 x x3 x
1) Determinazione del campo di esistenza (C.E.)
C.E. = R = xR : < x < +
19
y P3 x x3 x
2) Studio del segno della funzione
y 0 x3 x 0
raccogliendo la x
y 0 x x 2 1 0
trovando le soluzioni
dell’equazione associata
x x 2 1 0 x 0, x 2 1 0 x1 0, x2,3 1
20
x 0
x x 0 x 0, x 1 0
x 1, x 1
3
2
1
0
1
------------ ++++++++
++++++--------++++++
+
+
y<0
y>0 y<0
y>0
21
y P3 x x3 x
3) Intersezioni con gli assi
x 0
x 0
A 0,0 O
3
y 0
y x x
intersezione con l’asse y
B 0,0 A O
y 0
y 0
C 1,0
3
x1 0, x2 1, x3 1
0 x x
D 1,0
intersezioni con l’asse x
22
y P3 x x3 x
4) Limiti agli estremi del C.E.
C.E. = R = xR : < x < +
3
3
lim y lim x x lim x
3
x
x
x
3
3
lim y lim x x lim x
3
x
x
x
x+y+
xy
23
y P3 x x3 x
5) Calcolo della derivata prima
y ' D P3 x D x3 x D x3 D x 3x 2 1
6) Studio del segno della derivata prima
y ' 0 3x 2 1 0 x
1
3
1
1
1
1
,x
x
,x
3
3
3
3
1
3
+++ ------ +++
y > 0 y < 0 y > 0
M
m
24
y P3 x x3 x
x
1
3
3
3
è un minimo per la funzione
x
1
3
3
3
è un Massimo per la funzione
3
3
3
3 2 3
x
0,57 y
0,38
3
9
3 3
3
3
3
3
2 3
x
0,57 y
0,38
3
9
3 3
3 2 3
m
,
3
9
punto di minimo
3 2 3
M
,
3
9
punto di Massimo
25
y P3 x x3 x
7) Grafico della funzione
y
M
C
O D
m
x
26
Esempio 3
n=3
y P3 x x3 x 2 2 x 4
1) Determinazione del campo di esistenza (C.E.)
C.E. = R = xR : < x < +
27
y P3 x x3 x 2 2 x 4
2) Studio del segno della funzione
y 0 x3 x 2 2 x 4 0
scomponendo il
polinomio con Ruffini
1, 2, 4 sono i divisori del termine noto 4
x 1 P3 1 13 12 2 1 4 0
28
1 1 2 4
4
1
1 2
0
1 2 4
y P3 x x3 x 2 2 x 4 y P3 x x 1 x 2 2 x 4
trovando le soluzioni dell’equazione di
secondo grado associata al polinomio
x
2
2 x 4 0 x1,2 1 1 4 1 3
29
y 0 x3 x 2 2 x 4 0
x 1 x 2 2 x 4 0
x 1 0
x 1
y0 2
sempre
x 2x 4 0
1
------- +++++
+++++++++++
+
y<0
y>0
30
y P3 x x3 x 2 2 x 4
3) Intersezioni con gli assi
x 0
x 0
A 0, 4
3
2
y 4
y x x 2x 4
intersezione con l’asse y
y 0
y
0
y 0
x 1 0
2
3
2
0 x x 2 x 4
x 1 x 2 x 4 0
x2 2 x 4 0
y 0
x 1 B 1,0
mai
intersezione con l’asse x
31
y P3 x x3 x 2 2 x 4
4) Limiti agli estremi del C.E.
C.E. = R = xR : < x < +
3
2
3
lim y lim x x 2 x 4 lim x
3
x
x
x
3
2
3
lim y lim x x 2 x 4 lim x
3
x
x
x
x+y+
xy
32
y P3 x x3 x 2 2 x 4
5) Calcolo della derivata prima
y ' D P3 x D x3 x 2 2 x 4 3x 2 2 x 2
6) Studio del segno della derivata prima
y ' 0 3x 2 2 x 2 0 sempre
0
+++++++++++
y > 0
La funzione è sempre crescente!!!
Non ci sono né massimi né minimi!!!
33
y P3 x x3 x 2 2 x 4
7) Grafico della funzione
y
B
x
A
34
Osservazioni!
Le funzioni polinomiali sono definite su tutto R
C.E. = R = xR : < x < +
Le funzioni polinomiali non ammettono asintoti
né verticali né orizzontali
x+y
xy
35