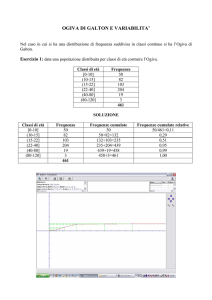
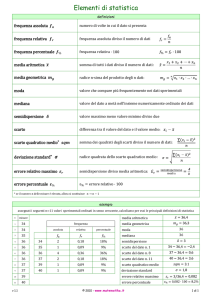
Elementi di Statistica – Lezione 3
=======================================================================
Statistica descrittiva
3. Indici di variabilità.
Gli indici di posizione non tengono conto della variabilità dei dati per cui insiemi
di dati aventi al stessa media possono presentare caratteristiche diverse.
La misura della variabilità de dati viene descritta con le seguenti funzioni:
I. Varianza.
II. Scarto quadratico medio o deviazione standard.
Si definisce varianza la quantità
σ2 =
1 n
2
( xi − M )
∑
n − 1 i =1
(1.1)
essendo M la media degli n valori dei dati.
Si definisce scarto quadratico medio o deviazione standard la radice
quadrata della varianza:
σ=
1 n
2
( xi − M )
∑
n − 1 i =1
(1.2)
La varianza e lo scarto quadratico medio misurano la variazione assoluta, rispetto alla
media, dell’insieme dei dati. In particolare lo scarto quadratico medio misura la
dispersione dei dati nella stessa unità di misura della media. Per questo motivo è
preferibile alla varianza. La media e la deviazione standard sono, rispettivamente,
l’indice di posizione e quello di dispersione più usati.
Epressioni alternative alla (1.1) sono:
1 ⎡ n 2
⎤
σ =
xi − n M 2 ⎥
∑
⎢
n − 1 ⎣ i =1
⎦
(1.3)
2
1 ⎡ n 2 1⎛ n ⎞ ⎤
σ =
⎢ ∑ xi − ⎜ ∑ xi ⎟ ⎥
n − 1 ⎢⎣ i =1
n ⎝ i =1 ⎠ ⎥⎦
(1.4)
2
ovvero
2
[esempio n.1.doc].
=======================================================================
Pag. 1
Elementi di Statistica – Lezione 3
=======================================================================
Volendo confrontare insiemi di dati determinati in diverse unità di misura può essere
utile usare una variazione relativa e non assoluta come la deviazione standard.
A tale scopo si usa il seguente valore (relativo):
Definizione : Coefficiente di variazione CV:
Il coefficiente di variazione CV è definito dalla quantità:
CV =
σ
M
⋅100%
(1.5)
ed è una misura relativa in quanto esprime lo scarto quadratico medio come
percentuale della media ed quindi una grandezza adimensionale.
Ad esempio: Un campione di 200 pacchi presenta variazioni di peso e di
volume aventi le seguenti misure:
1. peso medio M P = 9kg ;
2. d.s. del peso σ P = 1,5kg ;
3. volume medio mV = 2, 7m3 ;
4. d.s. del volume σ V = 0, 6m3 .
Calcolando i rispettivi coefficienti di variazione si ha:
1,5
⋅100% = 16, 67%
9
0, 6
• coeff. di variazione del volume : CVV =
⋅100% = 22, 22%
2, 7
• coeff. di variazione del peso : CVP =
Si deduce quindi che il volume dei pacchi ha una variabilità più forte
rispetto a quella dei pesi.
3. Media e varianza per dati raggruppati.
Pur se con la diffusione del computer e di programmi statistici a basso costo la
determinazione della media e della varianza di un numero grande di dati non presenta
difficoltà, a volte è utile o necessario studiare dati raggruppati in classi.
In tal caso, dopo aver raggruppato gli n dati k classi ed indicato con mi il valore
centrale della i-esima classe e con fi la corrispondente frequenza assoluta si
definisce Media dei dati raggruppati la quantità:
1 k
M = ∑ mi f i
n i =1
(1.6)
=======================================================================
Pag. 2
Elementi di Statistica – Lezione 3
=======================================================================
La varianza è data da:
σ2 =
1 ⎡ k
2
⎤
( mi − M ) fi ⎥
∑
⎢
n − 1 ⎣ i =1
⎦
(1.7)
o in forma alternativa:
2
1 ⎡ k
1⎛ k
⎞ ⎤
2
σ =
⎢ ∑ fi mi − ⎜ ∑ fi mi ⎟ ⎥
n − 1 ⎢⎣ i =1
n ⎝ i =1
⎠ ⎥⎦
2
(1.8)
ovvero:
1 ⎡ k
⎤
σ =
fi mi2 − n M 2 ⎥
∑
⎢
n − 1 ⎣ i =1
⎦
2
(1.9)
In [esempio n.1.xls] (ultimo foglio) vengono applicate le suddette formule (1.6) e (1.9)
ai dati del problema esempio n.2 della Lezione n.1.
In generale i valori ottenuti con i dati raggruppati sono una approssimazione di quelli
ottenuti operando su tutti i dati grezzi.
La media, la mediana e lo scarto quadratico medio hanno un ruolo importante nello
studio delle distribuzioni di frequenza che possono presentare forme diverse ma fra
queste le più importanti solo quelle che hanno un forma a “campana”.
Se la distribuzione è perfettamente simmetrica si dice di tipo “normale”, se non lo è
perfettamente i dati si dicono “approssimativamente normali” [Fig. 1].
Fig.1: istogramma simmetrico (a sinistra), dati approssimativamente normali (a destra)
Una distribuzione asimmetrica, detta anche obliqua, può avere una coda a destra
(asimmetria positiva) oppure a sinistra (asimmetria negativa).
=======================================================================
Pag. 3
Elementi di Statistica – Lezione 3
=======================================================================
Fig.2:distribuzione con asimmetria positiva (a destra) e con asimmetria negativa (a
sinistra)
Una misura della asimmetria viene data dal coefficiente di asimmetria di Pearson
definito da:
Siano M, m, σ rispettivamente la media, la mediana e lo scarto
quadratico medio di un insieme di dati: il coefficiente di asimmetria di
Pearson è definito da:
3( M − m )
(1.1)
SK =
σ
Se la media è maggiore della mediana ( SK > 0 ) la distribuzione dei dati ha
asimmetria positiva, caso contrario ( SK < 0 ) si ha asimmetria negativa. Ovviamente
per SK = 0 si ha perfetta simmetria. Osserviamo, per inciso, che SK è un valore
dimensionale.
La media e lo scarto quadratico medio forniscono importanti informazioni sulla
distribuzione dei dati, infatti vale a seguente regola empirica:
Un insieme di dati, approssimativamente normale, con media M e scarto
quadratico medio σ , presenta la seguente distribuzione:
1. circa i 68% dei dati è compreso fra M − σ e M + σ ;
2. circa il 95% dei dati è compreso fra M − 2σ e M + 2σ ;
3. circa il 99% dei dati è compreso fra M − 3σ e M + 3σ .
=======================================================================
Pag. 4