le funzioni goniometriche

FUNZIONE SENO
LEGGE:
nella calcolatrice o in un software di tipo matematico)
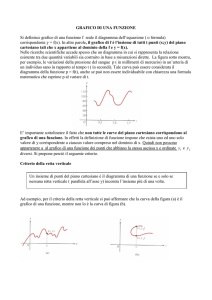
DOMINIO: R (l’intero insieme dei numeri reali)
CODOMINIO:
PERIODICITÀ: 2π (cioè
con kZ (k numero intero),
aumentando il valore dell’angolo α di un multiplo intero di 2π il valore del seno dell’angolo
non cambia).
GRAFICO
FUNZIONE RECIPROCA DELLA FUNZIONE SENO
È la funzione COSECANTE
LEGGE:
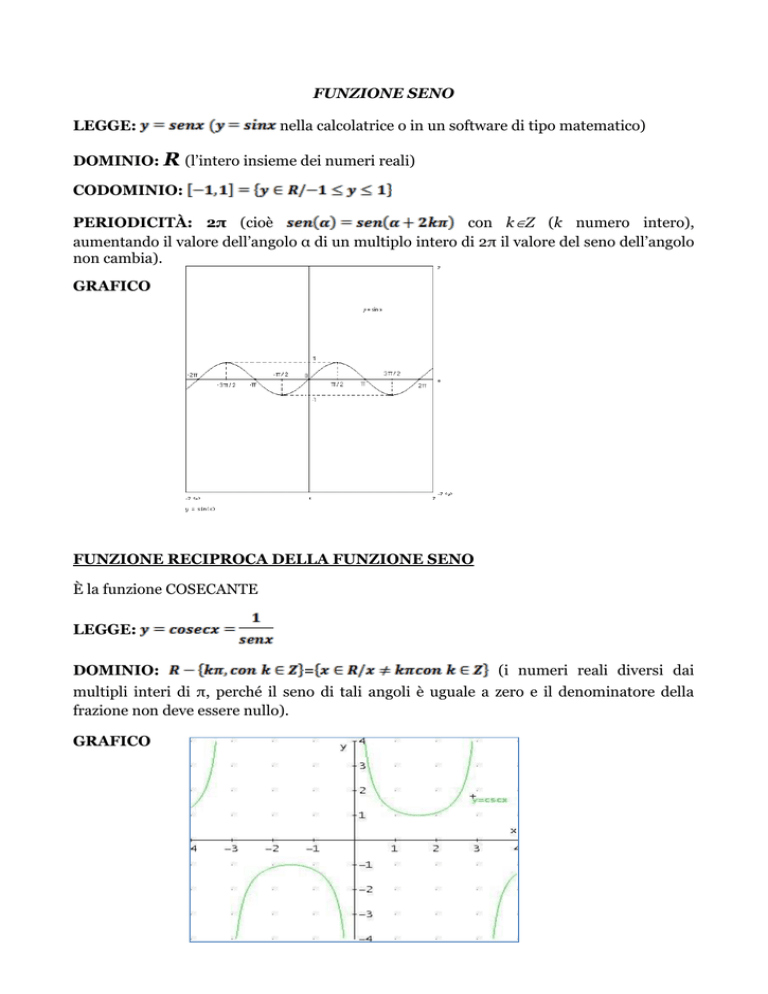
DOMINIO:
=
(i numeri reali diversi dai
multipli interi di π, perché il seno di tali angoli è uguale a zero e il denominatore della
frazione non deve essere nullo).
GRAFICO
1
FUNZIONE INVERSA DELLA FUNZIONE SENO
È la funzione ARCOSENO. la funzione seno non è invertibile nell’intero insieme dei
numeri reali perché non è biunivoca. Se consideriamo una restrizione di tale funzione
all’intervallo
in esso la funzione è crescente e invertibile. La funzione inversa ha le
seguenti caratteristiche:
LEGGE: y=arcsenx (nella calcolatrice y=sin-1x, in software applicativi come Derive
y=asinx). Se x è un numero reale maggiore o uguale a -1 e minore o uguale ad 1, l’arcoseno
di x rappresenta l’arco (angolo) compreso tra meno pi greco mezzi e più pi greco mezzi il
.
cui seno è uguale a quel numero. Ad esempio
DOMINIO:
CODOMINIO:
GRAFICO
Confronto tra il grafico della funzione seno limitatamente
all’intervallo
ed il grafico della funzione
arcoseno; si nota la simmetria dei due grafici rispetto alla
bisettrice del primo e terzo quadrante.
2
FUNZIONE COSENO
LEGGE:
(anche nella calcolatrice o in un software di tipo matematico)
DOMINIO: R (l’intero insieme dei numeri reali)
CODOMINIO:
PERIODICITÀ: 2π (cioè
con kZ (k numero intero),
aumentando il valore dell’angolo α di un multiplo intero di 2π il valore del coseno
dell’angolo non cambia).
GRAFICO
FUNZIONE RECIPROCA DELLA FUNZIONE COSENO
È la funzione SECANTE
LEGGE:
DOMINIO:
=
(i
numeri reali diversi da π/2 e dai relativi multipli, perché il coseno di tali angoli è uguale a
zero e il denominatore della frazione non deve essere nullo).
GRAFICO
3
FUNZIONE INVERSA DELLA FUNZIONE COSENO
È la funzione ARCOCOSENO. La funzione coseno non è invertibile nell’intero insieme dei
numeri reali perché non è biunivoca. Se consideriamo una restrizione di tale funzione
all’intervallo
in esso la funzione è decrescente e invertibile. La funzione inversa ha le
seguenti caratteristiche:
LEGGE: y=arccosx (nella calcolatrice y=cos-1x, in software applicativi come Derive
y=acosx). Se x è un numero reale maggiore o uguale a -1 e minore o uguale ad 1, l’arcoseno
di x rappresenta l’arco (angolo) compreso tra zero e pi greco il cui coseno è uguale a quel
numero. Ad esempio
.
DOMINIO:
CODOMINIO:
GRAFICO
Confronto tra il grafico della funzione coseno limitatamente all’intervallo
ed il grafico della funzione arcocoseno; si nota la simmetria
dei due grafici rispetto alla bisettrice del primo e terzo
quadrante.
4
(in verde il grafico della funzione coseno ed in nero il grafico della funzione arcocoseno).
FUNZIONE TANGENTE
LEGGE:
nella calcolatrice o in un software di tipo matematico)
DOMINIO:
=
CODOMINIO:
PERIODICITÀ: π (cioè
con kZ (k numero intero), aumentando il
valore dell’angolo α di un multiplo intero di π il valore della tangente dell’angolo non
cambia).
GRAFICO
FUNZIONE RECIPROCA DELLA FUNZIONE TANGENTE
È la funzione COTANGENTE
LEGGE:
DOMINIO:
(y=cotx in software applicativi come Derive)
=
(i numeri reali
diversi dai multipli interi di π, perché il seno di tali angoli è uguale a zero e il denominatore
della frazione non deve essere nullo).
5
CODOMINIO:
PERIODICITÀ: π
GRAFICO
FUNZIONE INVERSA DELLA FUNZIONE TANGENTE
È la funzione ARCOTANGENTE. La funzione tangente non è invertibile nell’intero
dominio perché non è biunivoca. Se consideriamo una restrizione di tale funzione
all’intervallo
in esso la funzione è invertibile. La funzione inversa ha le seguenti
caratteristiche:
LEGGE: y=arctgx (nella calcolatrice y=tan-1x, in software applicativi come Derive
y=atanx). Se x è un numero reale, l’arcotangente di x rappresenta l’arco (angolo) compreso
tra meno pi greco mezzi e pi greco mezzi (estremi esclusi) la cui tangente è uguale a quel
numero. Ad esempio
.
DOMINIO: R
CODOMINIO:
GRAFICO
6
Confronto tra il grafico della funzione tangente ed il grafico della funzione arcotangente; si
nota la simmetria dei due grafici rispetto alla bisettrice del primo e terzo quadrante.
(in verde il grafico della funzione tangente limitatamente
all’intervallo
ed in nero il grafico della funzione
arcotangente).
Da ricordare anche la funzione inversa della funzione COTANGENTE, cioè la funzione
ARCOCOTANGENTE, con le seguenti caratteristiche:
LEGGE: y=arcctgx (in software applicativi come Derive y=acotx). Se x è un numero reale,
l’arcocotangente di x rappresenta l’arco (angolo) compreso tra zero e pi greco (estremi
esclusi) la cui cotangente è uguale a quel numero. Ad esempio
DOMINIO: R
CODOMINIO:
GRAFICO
7
.