LE FUNZIONI CIRCOLARI INVERSE
La legge del moto armonico d = sin(t) può essere applicata in due modi:
- è dato il tempo t e calcolo la posizione d della pallina che si muove di moto armonico;
- è data la posizione d della pallina e ricavo il tempo t (come se l’oscillatore fosse un orologio).
Questo suggerisce, in matematica, di:
- pensare alla funzione circolare y = sin(x),
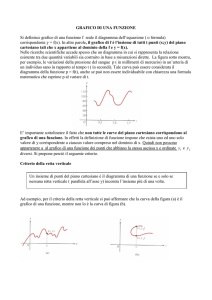
- scrivere la formula x = sin (y) e rappresentarla nel piano cartesiano, come
si vede qui a fianco a sinistra.
1. Risolvi i seguenti quesiti:
- spiega perché la figura a fianco non è il grafico di una sola funzione;
_______________________________________________________________
- nel grafico evidenza con una penna rossa l’arco più vicino ad O che fa
corrispondere una sola y ad ogni x scelta nell’intervallo [-1, 1] e osserva
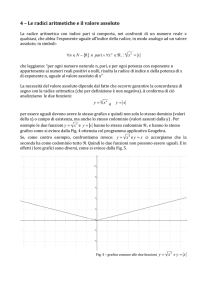
l’arco ridisegnato qui sotto.
La figura a destra mostra il grafico di una sola funzione, descritta qui sotto:
• Dominio D ≡ [-1, 1]
π π
• Codominio C ≡ − ,
2 2
• “y è l’arco il cui seno vale x”, frase che si riassume con la formula
y = arcsinx
€
La funzione y = arcsin(x) è la funzione inversa di y = sin (x)
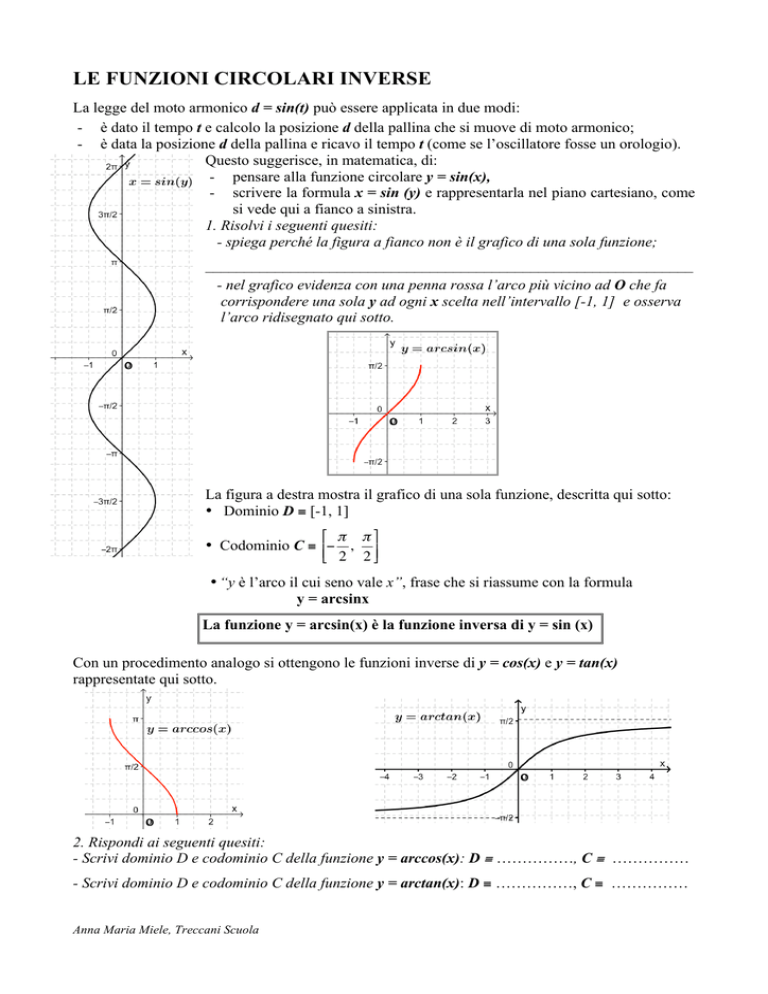
Con un procedimento analogo si ottengono le funzioni inverse di y = cos(x) e y = tan(x)
rappresentate qui sotto.
2. Rispondi ai seguenti quesiti:
- Scrivi dominio D e codominio C della funzione y = arccos(x): D ≡ ……………, C ≡ ……………
- Scrivi dominio D e codominio C della funzione y = arctan(x): D ≡ ……………, C ≡ ……………
Anna Maria Miele, Treccani Scuola