Programmazione a.s 2006-2007 - MATEMATICA - 2AL
OBIETTIVI
CONTENUTI
PREREQUISITI
Conoscenze
Competenze/
Capacità
STRUMENTI
VERIFICHE
Recupero e raccordo con
la 1classe del liceo
Conoscenze e
competenze della
scuola media
Recuperare e valorizzare le
conoscenze della classe I
Recuperare e valorizzare le competenze della
classe I
Riattivazione e
sistematizzazione
delle conoscenze
con esercizi
guidati, lavoro di
gruppo e problem
solving
Verifiche formative con
domande orali, controllo
compiti a casa, lavori di
gruppo.
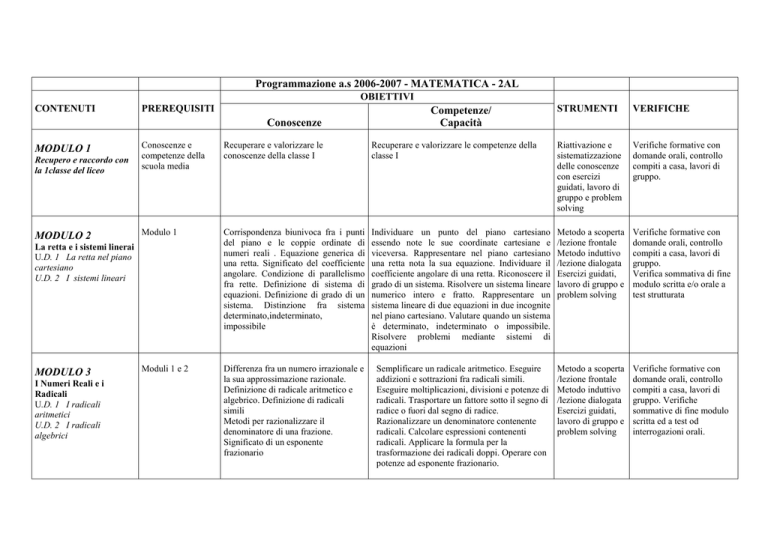
MODULO 2
Modulo 1
Corrispondenza biunivoca fra i punti
del piano e le coppie ordinate di
numeri reali . Equazione generica di
una retta. Significato del coefficiente
angolare. Condizione di parallelismo
fra rette. Definizione di sistema di
equazioni. Definizione di grado di un
sistema. Distinzione fra sistema
determinato,indeterminato,
impossibile
Individuare un punto del piano cartesiano
essendo note le sue coordinate cartesiane e
viceversa. Rappresentare nel piano cartesiano
una retta nota la sua equazione. Individuare il
coefficiente angolare di una retta. Riconoscere il
grado di un sistema. Risolvere un sistema lineare
numerico intero e fratto. Rappresentare un
sistema lineare di due equazioni in due incognite
nel piano cartesiano. Valutare quando un sistema
è determinato, indeterminato o impossibile.
Risolvere problemi mediante sistemi di
equazioni
Metodo a scoperta
/lezione frontale
Metodo induttivo
/lezione dialogata
Esercizi guidati,
lavoro di gruppo e
problem solving
Verifiche formative con
domande orali, controllo
compiti a casa, lavori di
gruppo.
Verifica sommativa di fine
modulo scritta e/o orale a
test strutturata
Moduli 1 e 2
Differenza fra un numero irrazionale e
la sua approssimazione razionale.
Definizione di radicale aritmetico e
algebrico. Definizione di radicali
simili
Metodi per razionalizzare il
denominatore di una frazione.
Significato di un esponente
frazionario
Semplificare un radicale aritmetico. Eseguire
addizioni e sottrazioni fra radicali simili.
Eseguire moltiplicazioni, divisioni e potenze di
radicali. Trasportare un fattore sotto il segno di
radice o fuori dal segno di radice.
Razionalizzare un denominatore contenente
radicali. Calcolare espressioni contenenti
radicali. Applicare la formula per la
trasformazione dei radicali doppi. Operare con
potenze ad esponente frazionario.
Metodo a scoperta
/lezione frontale
Metodo induttivo
/lezione dialogata
Esercizi guidati,
lavoro di gruppo e
problem solving
Verifiche formative con
domande orali, controllo
compiti a casa, lavori di
gruppo. Verifiche
sommative di fine modulo
scritta ed a test od
interrogazioni orali.
MODULO 1
La retta e i sistemi linerai
U.D. 1 La retta nel piano
cartesiano
U.D. 2 I sistemi lineari
MODULO 3
I Numeri Reali e i
Radicali
U.D. 1 I radicali
aritmetici
U.D. 2 I radicali
algebrici
MODULO 4
Moduli 1, 2 e 3
Forma normale di un’equazione di
secondo grado completa. Equazioni di
secondo grado incomplete. Formula
risolutiva di un’equazione di secondo
grado e la formula ridotta. Relazioni
fra le radici e i coefficienti di
un’equazione di secondo grado
completa. Significato di parametro.
Definizione di sistema di equazioni di
secondo grado
Riconoscere i vari tipi di equazioni di secondo
grado. Risolvere equazioni di secondo grado
numeriche intere e fratte. Applicare la formula
ridotta. Applicare le relazioni fra le radici e i
coefficienti di un’equazione di secondo grado
completa. Scomporre in fattori di primo grado
un trinomio di secondo grado. Risolvere quesiti
riguardanti equazioni parametriche di primo e
secondo grado. Risolvere equazioni di grado
superiore al secondo mediante la legge di
annullamento del prodotto. Risolvere sistemi di
secondo grado numerici di due equazioni in due
incognite.
Metodo a scoperta
/lezione frontale
Metodo induttivo
/lezione dialogata
Esercizi guidati,
lavoro di gruppo e
problem solving
Verifiche formative con
domande orali, controllo
compiti a casa, lavori di
gruppo. Verifiche
sommative di fine modulo
scritta ed a test od
interrogazioni orali.
Moduli 1 e 3
Definizioni di, disequazione.
Distinzione fra disequazione sempre
verificata e disequazione impossibile.
Definizione di sistema lineare di
disequazioni ad una incognita.
Equazione di una parabola con asse di
simmetria parallelo o coincidente con
l’asse y. Coordinate del vertice,
equazione dell’asse di simmetria.
Segno di un trinomio di secondo
grado. Disequazioni di secondo grado.
Applicare i principi di equivalenza delle
disuguaglianze. Risolvere una disequazione di
primo grado ad una incognita intera e fratta.
Rappresentare graficamente l’insieme delle
soluzioni di una disequazione e scriverlo anche
sotto forma di intervallo. Risolvere sistemi di
disequazioni lineari in una incognita.
Riconoscere e disegnare le curve di equazione y
= ax2
+ bx + c. Risolvere graficamente
un’equazione di secondo grado. Risolvere
graficamente sistemi di secondo grado
(intersezione retta parabola). Individuare
graficamente il segno di un trinomio di secondo
grado. Riconoscere dal grafico della parabola
associata a una disequazione di secondo grado le
soluzioni della disequazione stessa. Risolvere
disequazioni di secondo grado numeriche
Metodo a scoperta
/lezione frontale
Metodo induttivo
/lezione dialogata
Esercizi guidati,
lavoro di gruppo e
problem solving
Verifiche formative con
domande orali, controllo
compiti a casa, lavori di
gruppo. Verifiche
sommative di fine modulo
scritta ed a test od
interrogazioni orali.
Equazioni e sistemi di
equazioni di grado
superiore al I
U.D. 1 Equazioni di II
grado
U.D. 2 Equazioni di
grado superiore
U.D. Sistemi di II grado
MODULO 5
Le disequazioni lineari e
di secondo grado
U.D. 1 Le disequazioni di
I grado
U.D. 2 La parabola nel
piano cartesiano
U.D. 3 Le disequazioni di
II grado
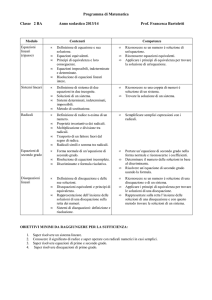
MODULO 5
Geometria Euclidea
U.D. 1 Superfici ed
equivalenza
U.D. 2 Le grandezze
geometriche
U.D. La similitudine
Sapere il concetto di equivalenza di
figure piane e le sue proprietà;
Conoscere il concetto di grandezze
commensurabili ed incommensurabili.
Sapere il significato di misura di una
superficie e i metodi per il calcolo
dell’area. Le definizioni di figure
simili e i criteri di similitudine dei
triangoli. I teoremi di Euclide ,
Pitagora, Talete
Applicare le proprieta’ dell’equivalenza nella
risoluzione di problemi.
Applicare i teoremi di Euclide, Pitagora ai
triangoli rettangoli.
Risolvere problemi di 2° grado con Euclide e
Pitagora. Applicare il teorema di Talete.
Metodo a scoperta
/lezione frontale
Metodo induttivo
/lezione dialogata
Esercizi guidati,
lavoro di gruppo e
problem solving
Verifiche formative con
domande orali, controllo
compiti a casa, lavori di
gruppo. Verifiche
sommative di fine modulo
scritta ed a test.