Esp2:E3 V 22/03/2013 10.05.00 m.
Corso di Laurea in Fisica
Esperimentazioni di Fisica II, a.a. 2013-2014
Scheda dell’Esercitazione n. 3 del 4 aprile 2014:
Studio della perturbazione introdotta dagli strumenti di misura
Scopo dell’esperienza
Lo scopo dell’esperienza è di quantificare e trattare la perturbazione introdotta dallo strumento di misura nello
studio della caduta di tensione lungo una catena di resistori.
Materiale a disposizione
Catena di N=10 resistenze di valore nominale eguale (R=56 kΩ).
Un generatore di tensione continua.
Strumento universale ICE
Multimetro digitale
Descrizione dell’esperienza
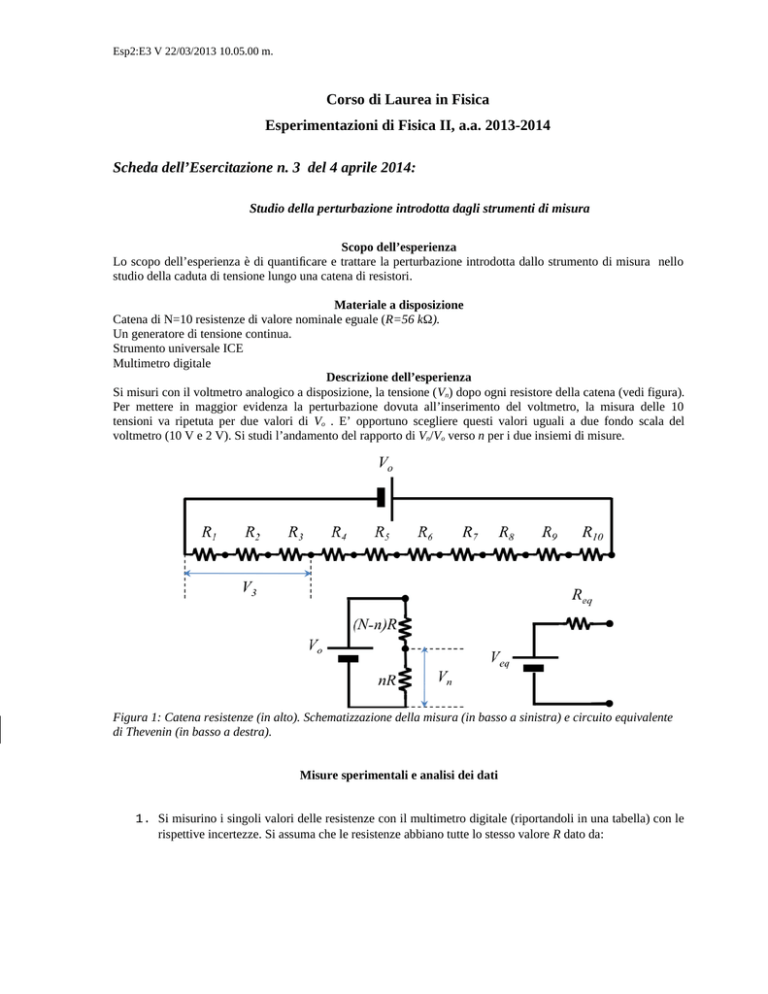
Si misuri con il voltmetro analogico a disposizione, la tensione (Vn) dopo ogni resistore della catena (vedi figura).
Per mettere in maggior evidenza la perturbazione dovuta all’inserimento del voltmetro, la misura delle 10
tensioni va ripetuta per due valori di Vo . E’ opportuno scegliere questi valori uguali a due fondo scala del
voltmetro (10 V e 2 V). Si studi l’andamento del rapporto di Vn/Vo verso n per i due insiemi di misure.
Figura 1: Catena resistenze (in alto). Schematizzazione della misura (in basso a sinistra) e circuito equivalente
di Thevenin (in basso a destra).
Misure sperimentali e analisi dei dati
1. Si misurino i singoli valori delle resistenze con il multimetro digitale (riportandoli in una tabella) con le
rispettive incertezze. Si assuma che le resistenze abbiano tutte lo stesso valore R dato da:
Esp2:E3 V 22/03/2013 10.05.00 m.
R=
1
N
∑R
i
i
media dei singoli valori misurati Ri, con un incertezza pari alla deviazione standard dei valori misurati.
2. Si monti il circuito e si misuri, con il multimetro analogico, Vnexp (n=1,…,10) per i due valori di Vo
scelti. Si riportino in tabella i valori sperimentali Vnexp , e i valori attesi Vn.
3. Riportare su di un grafico Vnexp/Vo e i valori attesi Vn/Vo (i valori sperimentali per i due fondo scala).
Commentare le differenze tra le misure effettuate con i due fondo scala.
4. Ricavare N-1 stime della Rv (vedi relazione nel punto 2 dello Studio teorico) per i due diversi fondo
scala scelti, ognuno con la sua incertezza. Si ricavi la stima migliore di Rv , calcolando la media pesata
delle N-1 misure con la sua incertezza. Si confronti il risultato ottenuto con i valori nominali dell’ICE e
si commenti il risultato.
5. Si calcoli, nota Rv dalla media pesata del punto precedente, la correzione Cn con la relativa incertezza ed
i valori corretti Vncorr = Vnexp (1 + Cn) con le loro incertezze; si confrontino tali valori con quelli attesi Vn .
Studio teorico
Per studiare il circuito è utile adottare lo schema equivalente di Thévenin per il partitore di tensione come
mostrato in figura 1: per un dato n la Vneq è la tensione di circuito aperto tra A e B, mentre Rneq è la resistenza tra
A e B calcolata sostituendo il generatore Vo con un corto circuito.
1- Per il circuito equivalente di Thevenin si ha:
V eqn = V 0
n
= Vn
N
e
1
1
1
=
+
n
Rn RN −n
Req
con Rn = nR e RN-n = (N − n)R.
2- In queste condizioni si può calcolare che, se con Rv indichiamo la resistenza interna del voltmetro, la caduta di
tensione che ci si aspetta di misurare dopo n resistenze ( Vnexp ) è data da:
Vnexp =
V0
R N
( N - n ) +ᅠ
Rv n
3- L’equazione precedente mostra come la misura sia affetta da un effetto sistematico tanto maggiore quanto
minore è Rv. La valutazione quantitativa di questo effetto sistematico è data dalla quantità Cn (correzione
relativa):
ᅠ
Cn =
Vn - Vnexp n ( N - n ) R
=
Vnexp
NRv
Si può notare che, essendo Req = nR(N − n)/N , l’errore relativo introdotto dallo strumento di misura si può anche
scrivere come:
ᅠ
Esp2:E3 V 22/03/2013 10.05.00 m.
Cn =
Req
Rv
Quindi avendo a disposizione una misura sperimentale Vexpn posso ricavare il valore corretto una volta nota la
correzione Cn:
ᅠ
Vncorr = Vnexp (1+ Cn )
e Vncorr dovrà essere eguale al valore teorico (imperturbato) Vn (a meno delle incertezze su R, Rv , Vnexp).
ᅠ