Attività di laboratorio.
“Verifica della prima e seconda legge di Ohm
ed effetto joule.”
Classe di concorso A49
Bernardi Eros
Anno 2006/2007
“Esperienza di laboratorio”.
Verifica della prima e seconda legge di Ohm ed effetto joule.
Prerequisiti.
•
Sapere che cosa significa diretta proporzionalità.
•
Sapere che cosa significa proporzionalità inversa.
•
Sapere cosa sono i conduttori e gli elettroni di conduzione.
•
Funzionamento di un circuito elettrico.
•
Funzione del generatore e di differenza di potenziale.
•
Conoscere la definizione e l’unità di misura differenza di potenziale, intensità di corrente
elettrica.
•
Conoscere la prima e seconda legge di Ohm .
•
Leggi fondamentali della termologia.
Obiettivi.
•
Significato di corrente elettrica e unita di misura della sua intensità.
•
Funzione del generatore di tensione.
•
Funzione del potenziometro.
•
Funzionamento degli strumenti di misura(amperometro e voltmetro).
•
Caratteristiche di un circuito elettrico.
•
Enunciato della prima e seconda legge di Ohm.
•
Significato di misura della resistenza elettrica.
•
Caratteristiche generali dei conduttori.
•
Calcolare il calore specifico dell’acqua.
•
Verifica sperimentale de calore specifico.
1
Voltmetro.
Lo strumento che misura la differenza di potenziale tra due punti di una resistenza attraversata da
corrente elettrica si chiama voltmetro.
Lo strumento deve essere inserito in parallelo con la resistenza, i morsetti dello strumento devono
essere collegati alle estremità della resistenza incognita, è necessario che l’inserimento del
voltmetro nel circuito non alteri apprezzabilmente l’intensità di corrente che attraversa la resistenza,
per cui il voltmetro deve essere attraversato da una piccola intensità di corrente quindi deve avere
una alta resistenza interna.
Se la corrente che attraversa il voltmetro è inferiore all’errore assoluto sulla misura di quest’ultima
allora possiamo considerare il voltmetro.
Voltmetro utilizato.
Il tester della fotografia precedente sarà utilizzato come voltmetro a corrente continua quindi un
primo cavetto sarà collegato nel simbolo di corrente continua
Utilizzeremo alternativamente il tester con porta 10V ed 2V collegando il secondo cavetto nel foro
con le relative scritte. Dalla figura si osserva che il tester è suddiviso in 50 intervalli questo implica
che utilizzando come portata 10v la sensibilità dello strumento risulta di 0,2V/divisione, mentre per
una portata di 2V risulta 0,04V/divisione.
La classe dello strumento esprime l’errore relativo percentuale che lo strumento commette sulla
misura massima cioè portata; la classe dello strumento ci permette di calcolare l’errore assoluto
sulla misure infatti si ha Ea=(classe/100) · portata.
2
Considerato che la classe del nostro tester è 1,5 abbiamo i seguenti errori assoluti:
Ea =
1,5
⋅ 10V = 0,15V ≅ 0,2V
100
Ea =
1,5
⋅ 2V = 0,03V ≅ 0,04V
100
Considerati questi calcoli assumiamo come errore assoluto la sensibilità dello strumento.
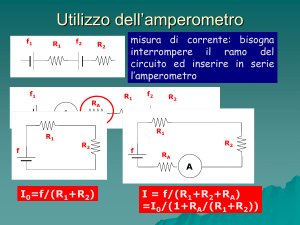
Amperometro.
Per rivelare qualitativamente l'intensità di corrente che attraversa un circuito è sufficiente inserire
una lampadina; dalla luminosità del filamento possiamo avere informazioni sulla intensità di
corrente. Se invece vogliamo quantificare la misura è necessario, inserire un amperometro (A) o
un milliamperometro (mA) se si tratta di correnti dell'ordine del milliampere. Poiché un
amperometro misura l'intensità di corrente che lo attraversa, esso deve essere inserito in serie con la
resistenza, in modo che strumento di misura e resistenza siano attraversati dalla stessa intensità di
corrente.
Poiché lo strumento di misura presenta una resistenza interna r, il suo inserimento nel circuito fa
aumentare la resistenza totale. Di conseguenza, l'amperometro misura una corrente di intensità
minore di quella che volevamo misurare. Affinché la perturbazione indotta nel circuito sia
trascurabile, è necessario che la resistenza interna dell'amperometro sia piccola rispetto alla
resistenza del circuito in cui si vuole misurare l'intensità di corrente.
Amperometro utilizzato.
Questi strumenti vengono comunemente chiamati tester in quanto possono essere usati a seconda
dei casi sia da amperometri oppure voltmetri.
Per quanto gia detto prima visto che la classe del nostro tester è 1,5 abbiamo i seguenti errori
assoluti:
Ea =
1,5
⋅ 0.3 A = 0,0045 A ≅ 0,005 A
100
3
Ea =
1,5
⋅ 1,5 A = 0,0225 A ≅ 0,03 A
100
Considerati questi calcoli assumiamo come errore assoluto la sensibilità dello strumento.
Reostato.
B
C
V
A
IL REOSTATO COME POTENZIOMETRO.
La figura rappresenta simbolicamente un reostato, i cui due morsetti A e B sono collegati ai poli di
un generatore. Tra il morsetto A e il cursore C è inserito un voltmetro. Con tale collegamento
diciamo che il reostato è inserito come potenziometro.
Spostando il cursore da A a B, il voltmetro segna una tensione crescente da zero a un massimo, il
cui valore dipende dalla forza elettromotrice del generatore. Il massimo valore della tensione
4
coincide infatti con la d.d.p. V0 esistente tra A e B ed è perciò uguale, a meno della caduta ohmica
sulla resistenza interna del generatore, alla f.e.m. del generatore. Infatti la corrente che attraversa il
reostato di resistenza complessiva R è:
I=
V0
R
Se indichiamo con R1 la parte della resistenza compresa tra A e C, la d.d.p. tra gli stessi punti è:
V1 = IR1
Tenendo conto dell'espressione di I si ha perciò:
V1 =
R1
V0
R
Dalla precedente si ha in particolare:
a) Per C ≡ A è R1 = 0 e quindi V1 = 0
b) Per C ≡ B è R1 = R e quindi V1 = V0
Quando il cursore occupa una posizione intermedia tra A a B, anche la d.d.p. Vi assume un valore
intermedio tra zero e Vo. Se, per esempio, il generatore è una batteria da 12 volt con resistenza
interna trascurabile, possiamo ottenere tutte le tensioni variabili con continuità da zero a 12 volt con
le quali è possibile alimentare un qualsiasi circuito.
5
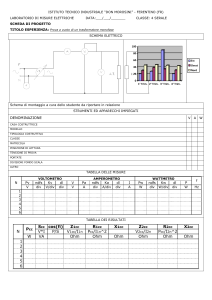
Modalità del lavoro in laboratorio
a) Suddividere la classe in gruppi di lavoro.
b) Consegna del materiale di lavoro delle schede di laboratorio con le istruzioni per il
montaggio del circuito.
c) Spiegare tutti i simboli utilizzati in un circuito elettrico.
d) Predisporre un foglio con il materiale consegnato ai vari gruppi in modo da controllare il
materiale che restituiranno.
e) Accertarsi che tutti siano in grado di assemblare correttamente il circuito.
f) Se eventualmente qualcuno commette errori, portarlo a comprendere cosa e perché il
circuito non potrebbe funzionare.
g) Verificare il giusto posizionamento degli strumenti di misura.
h) A questo punto si possono azionare le prese del laboratorio in modo che inizino con il
lavoro.
i) Monitorare i vari gruppi.
j) Cercare di terminare le operazioni di misura dei vari esperimenti qualche minuto prima del
suono delle campanella in modo che con calma sia restituito tutto il materiale di laboratori.
6
Verifica della Prima legge di Ohm
Misura di una resistenza incognita.
A
A
C
E
I
∆VEF
V
B
F
Strumenti e apparecchiature utilizzati.
-
-
-
-
Generatore di tensione continua, con potenziometro per prelevare una tensione variabile(∆VCB)
220V in ingresso, 0 ÷12V in uscita.
Tester usato come voltmetro con cavetti e puntali:
Portata utilizzata = 10V ; 2V
Numero di divisioni = 50div
Sensibilità = 0,2V/div ; 0,04V/div
Classe = 1,5
Resistenza interna 200000Ω
Amperometro a zero centrale con più portate:
Portata utilizzata = 1,5A ; 0,3A
Numero di divisioni = 30
Sensibilità =0,05A/div ; 0,01A/div
Classe = 1,5
Resistenza interna 0,76Ω
Filo di costantana, omogeneo e calibrato, di resistenza incognita:
Lunghezza =1m
Diametro = 2·10-4m
Due serrafili su piede a bottone.
Tre cavetti di collegamento.
Metro metallico.
7
Leggenda
-
I
Intensità di corrente elettrica che percorre il conduttore.
-
∆VEF
Differenza di potenziale fra gli estremi del conduttore.
-
R
Resistenza del conduttore alla temperatura di lavoro.
Introduzione all’esperimento di laboratorio ed utilizzo
appropriato delle apparecchiature.
-
Il reostato usato come potenziometro dopo ogni lettura deve essere azzerato.
-
Le letture sul amperometro e voltmetro devono essere prese il più rapidamente possibile in
modo che il filo di costantana non si surriscaldi.
-
Lasciare un po’ di tempo tra una lettura e l’altra in modo che il filo di costantana torni alla
temperatura ambiente.
Tabella l’utilizzatore è un filo di costantana di lunghezza un metro
kv
Nv
V/div Div
∆VEF ± Ea
Er∆VEF
Volt
ka
Na
I ± Ea
A/div Div
ErI
Ampere
∆VEF/ I ± Ea
Er∆VEF/ I
Ohm
0,04
20
(0,80±0,04)V
0,05
0,01
5
(0,05±0,01)A
0,2
(16±4)Ω
0,25
0,04
40
(1,60±0,04)V
0,025
0,01
10
(0,10±0,01)A
0,1
(16±2)Ω
0,15
0,2
12
(2,4±0,2)V
0,08
0,01
15
(0,15±0,01)A 0,07
(16±2)Ω
0,15
0,2
20
(4,0±0,2)V
0,05
0,01
25
(0,25±0,01)A 0,04
(16±1)Ω
0,9
0,2
44
(8,8±0,2)V
0,02
0,05
11
(0,55±0,05)A 0,09
(16±2)Ω
0,1
∆VEF/ I ± Ea
Er∆VEF/ I
Tabella assegnata agli studenti da completare.
kv
Nv
V/div Div
0,04
20
0,04
0,2
8
∆VEF ± Ea
Volt
Er∆VEF
ka
A/div Div
0,01
0,01
12
Na
10
0,01
0,2
0,01
25
0,2
0,05
11
I ± Ea
Ampere
ErI
Rappresentazione grafica dei risultati.
Mediante l’utilizzo di excel realizzare il grafico che lega l’intensità alla differenza di potenziale.
Riportando sull’asse x l’intensità in ampere e su l’asse y la differenza di potenziale in volt.
10
y = 16x
Differenza di Potenziale(V)
9
8
7
6
5
4
3
2
1
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
Intensità(A)
Dopo di che realizzare lo stesso grafico su carta millimetrata.
9
Rappresentazione grafica su carta millimetrata
Domande e Conclusioni
1) Come risulta il rapporto fra la differenza di potenziale applicata agli estremi del conduttore e la
intensità di corrente che la percorre, entro i limiti del suo errore assoluto?
2) Cosa rappresenta la pendenza della retta con questa scelta degli assi cartesiani.
3) Quale legge di proporzionalità lega le due grandezze variabili?
4) Calcolare dal grafico la differenza di potenziale da applicare agli estremi del conduttore per
ottenere una intensità di 0,5A?
5) Calcolare dal grafico l’ intensità di corrente che deve percorrere un filo se ai suoi capi è
applicata una differenza di potenziale di 5V?
6) Quali sono le differenzi immediate tra i due grafici?
10
Misura di un campo elettrico uniforme.
Riportare tre punti E1,E2,E3 sul filo di costantana tramite l’utilizzo di un metro metallico piegando
leggermente il filo, in modo che il filo di lunghezza un metro risulti diviso in quattro parti uguali. A
questo punto dare una differenza di potenziale agli estremi del filo di costantana di 8 volt.
Suddivisione del filo di costantana.
E1
E
E3
F
E2
Con prudenza sfilare il collegamento del voltmetro dal punto E, ed posizionarlo prima sul punto E1
poi su E2 ed su E3, ed completare la tabella seguente.
∆V
Volt
metri
Er
∆V/I
E1F
E2F
E3F
(8,0±0,2)
(6,0±0,2)
(4,0±0,2)
(2,0±0,2)
0,025
Er
I
EF
Er
0.05
0.1
(1,000±0,001) (0,750±0,001) (0,500±0,001) (0,250±0,001)
0,001
V/m
0,033
(8,0±0,2)
0,026
0,001
(8,0±0,3)
0,034
0,002
(8,0±0,4)
0,052
0.004
(8,0±0,8)
0,104
Misurare il campo elettrico che i generatore produce all’interno del filo conduttore omogeneo e
calibrato; che caratteristiche ha?
11
Ripetere le misure dell’esercizio precedente con due fili di costantana di lunghezza un metro prima
in serie poi in parallelo.
Accertarsi che i gruppi di lavoro sappiano predisporre resistenze in serie ed in parallelo.
A questo punto si chiede ai gruppi di studenti se possono fare delle previsioni?
Tabella l’utilizzatore è due fili di costantana di lunghezza un metro in parallelo.
kv
Nv
V/div Div
∆VEF ± Ea
Er∆VEF
Volt
0,04
20
(0,80±0,04)V
0,04
40
(1,60±0,04)V
0,2
12
(2,4±0,2)V
0,2
20
(4,0±0,2)V
0,2
44
(8,8±0,2)V
ka
Na
A/div Div
I ± Ea
ErI
∆VEF/ I ± Ea
Ampere
Er∆VEF/ I
Ohm
Tabella l’utilizzatore è due fili di costantana di lunghezza un metro in serie.
kv
Nv
V/div Div
∆VEF ± Ea
Er∆VEF
Volt
0,2
12
(2,4±0,2)V
0,2
20
(4,0±0,2)V
0,2
44
(8,8±0,2)V
Le previsioni sono state confermate?
12
ka
Na
A/div Div
I ± Ea
Ampere
ErI
∆VEF/ I ± Ea
Ohm
Er∆VEF/ I
Resistenza interna di un generatore
Verifica della Prima legge di Ohm per il generatore.
Schema A (circuito aperto)
A
∆V0
V
Resistenza
interna del
generatore
B
Schema B (circuito chiuso)
A
C
A
I
∆V0
Rn
V
Resistenza
interna del
generatore
B
D
13
Elenco del materiale e relativa caratteristiche:
-
-
-
-
Generatore di tensione 0 ÷25V.
Tester usato come voltmetro con cavetti e puntali:
Portata utilizzata = 10V
Numero di divisioni = 50div
Sensibilità = 0,2V/div
R=20000Ω
Amperometro a zero centrale con più portate:
Portata utilizzata = 0,3A
Numero di divisioni = 30
Sensibilità = 0,01A/div
R=0,76Ω
Resistore con Rn=20Ω±1%
Leggenda
-
Rig : resistenza interna al generatore.
∆Vig : caduta di potenziale interna al generatore.
Misure:
A) A circuito aperto si legge sul tester ∆V0= (8,0±0,2)V
B) A circuito chiuso si legge sul tester ∆V= (5,8±0,2)V e sull’amperometro IA=(0,28±0,01)A
Elaborazioni dei dati
Caduta di potenziale sulla resistenza interna del generatore:
∆Vig =∆V0-∆V= 8,8-5,8=(2,2±0,2)V
Rig =
∆Vig
2,2V
=
= 7,9Ω
IA
0,28 A
⎛ 0,4 0,01 ⎞
+
Ea(Rig)=Er·Rig= ⎜
⎟ ⋅ 7,9Ω = 1,7Ω
⎝ 2,2 0,28 ⎠
La resistenza interna al generatore non è ohmica, cioè non è costante al variare della intensità che
la attraversa.
14
Limiti del metodo voltmetro-amperometro.
∆V ⎞
⎛
Il metodo utile alla misura di una resistenza Rx ⎜ Rx =
⎟ mediante la lettura su due strumenti è
I ⎠
⎝
difettoso, ovvero:
a) Con il voltmetro
Serve un voltmetro con RV >>>>>> Rx , perché RV è in parallelo ad Rx ; altrimenti:
1
1
1
=
+
RT Rx RV
1
1
1
R − RT
=
−
= V
Rx RT RV
RV ⋅ RT
Rx =
RV ⋅ RT
RV
= RT ⋅
RV − RT
RV − RT
Rx =
RV
∆V
⋅
I RV − ∆V
I
b) Con l’amperometro
Serve un amperometro con RA <<<<<<< Rx , perché RA è in serie con Rx ; altrimenti:
Rx =
∆V
− RA
I
15
Verifica della Seconda legge di Ohm
Resistenza di un filo omogeneo e calibrato in funzione della lunghezza.
Resistenza di un filo omogeneo e calibrato in funzione della sezione.
Misura della resistenza specifica di un materiale.
A
A
C
E
I
∆VEF
V
B
F
Strumenti e apparecchiature utilizzati.
-
-
-
-
16
Generatore di tensione continua, con potenziometro per prelevare una tensione variabile(∆VCB)
220V in ingresso, 0 ÷12V in uscita.
Tester usato come voltmetro con cavetti e puntali:
Portata utilizzata = 10V ; 2V
Numero di divisioni = 50div
Sensibilità = 0,2V/div ; 0,04V/div
Classe = 1,5
Amperometro a zero centrale con più portate:
Portata utilizzata = 1,5A,0.3A
Numero di divisioni = 30
Sensibilità =0,05A/div ; 0,01A/div
Classe = 1,5
Fili di costantana, omogenei e calibrati, di resistenza incognita e di
diametro = 2·10-4m , 3·10-4m,4·10-4m
Filo di rame, omogeneo e calibrato, di resistenza incognita e di diametro = 2·10-4m.
Filo di ferro, omogeneo e calibrato, di resistenza incognita e di diametro = 2·10-4m.
Due serrafili su piede a bottone.
Tre cavetti di collegamento.
Metro metallico millimetrato.
Leggenda
-
I
∆VEF
R
L
Intensità di corrente elettrica che percorre il conduttore.
Differenza di potenziale fra gli estremi del conduttore.
Resistenza del conduttore alla temperatura di lavoro.
Lunghezza del filo.
Procedimento.
Dopo avere eseguito il montaggio del circuito con filo di 0,500m di lunghezza, si posiziona il
cursore del reostato usato come potenziometro a zero (C su B) e quindi si attiva il generatore
tramite il tasto; si sposta il cursore in modo da applicare agli estremi del filo conduttore una d.d.p.
tale che alimenti in esso una corrente di circa 25 divisioni della scala dell’amperometro.
Si registrino in tabella A le misure lette sul voltmetro ed amperometro, si rimette il cursore a zero e
si spegne il generatore.
Si varia la lunghezza del filo e si ripete l’operazione.
Tabella A filo di costantana di diametro 0,2mm e lunghezza variabile
L± Ea
∆VEF ± Ea
kv
Er∆VEF
Nv
metri
V/div
0,2
I ± Ea
Volt
A/div
(2,0±0,2)V
0,2
0,1
0,01
(6,0±0,2)V
0,2
0,03
0,05
(9,0±0,2)V
0,2
0,02
0,05
(3,8±0,2)V
0,2
(0,25±0,01)A 0,04
(8,0±1,1)Ω
0,14
(0,50±0,05)A 0,08
(12,0±1,3)Ω
0,11
(0,60±0,05)A 0,08
(15,0±1,5)Ω
0,10
0,05
0,01
(0,20±0,01)A 0,05
(19,0±1,9)Ω
0,10
(0,15±0,01)A 0,07
(22.6±2,9)Ω
0,13
20
(3,4±0,2)V
17
Ohm
12
19
1,500±0,001
Ampere
10
45
1,250±0,001
Er
25
30
1,000±0,001
R ± Ea
div
10
0,750±0,001
ErI
Na
div
0,500±0,001
ka
0,06
0,01
15
17
Tabella assegnata agli studenti da completare.
L± Ea
kv
∆VEF ± Ea
ka
Er∆VEF
Nv
metri
I ± Ea
ErI
R ± Ea
Na
V/div
Volt
A/div
div
Ampere
Ohm
div
0,500±0,001
0,750±0,001
1,000±0,001
1,250±0,001
1,500±0,001
Rappresentazione grafica dei risultati.
Mediante l’utilizzo di excel realizzare il grafico che lega la lunghezza del filo alla resistenza,
30
Resistenza(Ohm)
25
y = 15,227x
20
15
10
5
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
Lungheza(m)
18
1
1,1
1,2
1,3
1,4
1,5
1,6
Er
Tabella B filo di costantana di lunghezza un metro e diametro variabile.
d
S
kv
Nv
∆VEF ± Ea
ka
Na
R ± Ea
I ± Ea
Er
Er
R·S ± Ea
Er
Er
mm
mm2
V/div
Div
Volt
A/div
Div
Ampere
Ohm
Ohm· mm2
0,2
0,0314
0,2
12
(2,4±0,2)V
0,01
15
(0,15±0,01)A
(16±1)Ω
(0.50±0.04)
0,01
0,3
0,0707
0,04
28
(1,12±0,04)V
0,01
15
0,04
0,4
0,1256
0,04
39
(1,56±0,04)V
0,05
8
0,07
0,08
0,08
(0,15±0,01)A
(7,5±0,8)Ω
(0.53±0,06)
0,07
0,11
0,11
(0,40±0,05)A
(3,9±0,5)Ω
(0,49±0,05)
0,1
0,13
0,13
0,03
Tabella assegnata agli studenti da completare.
d
S
kv
Nv
∆VEF ± Ea
ka
Na
Er
Er
mm
mm2
0,2
0,0314
0,3
0,0707
0,4
0,1256
V/div
Div
Volt
R ± Ea
I ± Ea
A/div
Div
Ampere
R·S ± Ea
Er
Ohm
Er
Ohm· mm2
19
Rappresentazione grafica dei risultati.
Mediante l’utilizzo di excel realizzare il grafico dei dati.
18
16
Resistenza(Ohm)
14
12
10
8
6
4
2
0
0
0,02
0,04
0,06
0,08
0,1
0,12
0,14
Sezione(millimetri quadrati)
Domande.
1) Dedurre dal grafico la legge che lega la sezione ed la resistenza?
2) Come risulta il prodotto fra la sezione del filo e la sua resistenza?
3) I dati e la verifica confermano la legge?
4) Calcola il valor medio del prodotto della resistenza per la sezione ed utilizzalo per calcolare
la resistenza di un filo di costantana di lunghezza un metro e diametro un millimetro?
Tabella C fili di vario materiale di lunghezza un metro e diametro 0,0314mm2.
Materiale
kv
Nv
∆VEF ± Ea
ka
Na
Er
Er
Costantana
Volt
A/div
Div
Ampere
Ohm
Ohm· mm2
0,2
12
(2,4±0,2)V
0,01
15
(0,15±0,01)A
(16±1)Ω
(0,50±0.04)
0,04
15
(1,12±0,04)V
0,04
40
(1,60±0,04)V
0,03
20
Er
Div
0,05
15
0,04
Ferro
Er
R·S ± Ea
V/div
0,01
Rame
R ± Ea
I ± Ea
0,05
10
0,07
0,08
0,08
(0,75±0,05)A
(0,69±0,08)Ω
(0,023±0,003)
0,07
0,11
0,11
(0,50±0,05)A
(3,2±0,4)Ω
(0,10±0,01)
0,1
0,13
0,13
Tabella assegnata agli studenti da completare.
Materiale
kv
Nv
∆VEF ± Ea
ka
Na
Er
Er
V/div
Div
Volt
R ± Ea
I ± Ea
A/div
Div
Ampere
R·S ± Ea
Er
Ohm
Er
Ohm· mm2
Costantana
Rame
Ferro
Domande.
1) Che grandezza caratteristica di ognuno dei tre metalli conduttori esaminati ci fornisce il
prodotto R·S della tabella C?
2) Quale è il suo significato fisico?
3) Quale è il miglior conduttore fra quelli esaminati?
4) Porta le misure di R·S nel sistema internazionale?
5) Visto che il filo si è scelto unitario dove possiamo trovare tale valore sul libro di testo?
21
Misura di una resistenza incognita con il
metodo ponte a filo
Rx
A
RAC
C
mA
D
RCA
B
Rn
Elenco del materiale e relativa caratteristiche:
-
-
Generatore di tensione continua 220V in ingresso, 0 ÷25V in uscita.
Sette cavetti di collegamento e un morsetto.
Filo di costantana diametro 0,4mm lunghezza 1,5m(omogeneo e calibrato)
Due serrafili su piede a bottone.
Due resistenze campione:
50Ω±1%
20Ω±1%
Resistenza incognita con spinotti.
Basetta con numero otto boccole(per inserire Rx e le due note)
Milliamperometro a zero centrale Portata=0,03A KA=0,001°/div
Nastro millimetrato Portata=2m Ks=0,001m/div
Leggenda
-
22
Rn
Rx
RAC
RCB
L1
L2
: resistenza nota (RDB) realizzata con due resistenze campione.
: resistenza incognita(RAD)
: resistenza del tratto AC del filo di costantana.
: resistenza del tratto CB del filo di costantana.
: lunghezza del tratto AC.
: lunghezza del tratto CB.
Procedimento
-
Si sceglie una resistenza nota dell’ordine di grandezza di RX.
Si esegue il montaggio del circuito come da schema, posizionando il cursore C(becco a
coccodrillo) a metà di AB.
Si attiva il generatore, evitando di superare per le resistenze RX e Rn l’intensità di I massima
consentita e senza mandare fuori scala il milliamperometro.
Si sposta il cursore C, cercando la posizione per cui l’intensità segnalata è nulla.
Si misura la lunghezza di AC e CB del filo di costantana ben teso più volte.
Metodo
Il ponte di Wheatstone è un dispositivo elettrico inventato da Samuel Hunter Christie e perfezionato
da Charles Wheatstone che permette di misurare in modo preciso il valore di una resistenza
elettrica.
Schema di un ponte di Wheatstone
Si compone di un generatore di tensione che alimenta due rami resistivi posti in parallelo: il primo è
composto da un resistore campione in serie a una cassetta di resistori (resistenza variabile tramite
opportune manopole) di elevata precisione; il secondo ramo è invece composta da un resistore
campione in serie alla resistenza incognita. Si pone quindi un galvanometro a zero centrale,, tra i
due resistori del primo ramo e i due del secondo ramo. Alimentando quindi il circuito, si noterà che
il galvanometro segnala il passaggio di una corrente. Variando il valore della cassetta di resistenze
fino a azzerare la corrente passante per il galvanometro (equilibrando quindi il ponte), si otterrà
l'esatto valore di resistenza elettrica del resistore incognito.
23
Se analizziamo lo schema del Ponte vediamo che, Rx é il resistore il cui valore di resistenza elettrica
vogliamo determinare, R1 e R3 sono resistori di valore fisso e noto, mentre il resistore R2 é variabile.
Se la relazione dei due resistori del lato conosciuto R2/R1 é uguale alla relazione degli altri due
resistori del lato non noto Rx/R3, la differenza di potenziale elettrico tra i due punti intermedi sarà
nulla e pertanto non circolerà nessuna corrente elettrica fra questi due punti. Per effettuare la misura
si fa variare il resistore R2 fino ad ottenere il punto di equilibrio.
Nell’esperimento del ponte a filo spostando il becco a coccodrillo del punto C otteniamo che tra il
punto C ed D la differenza di potenziale sia nulla per cui abbiamo:
⎛ l ⎞ ⎛ l ⎞
Rx : Rn = RAC : RCB = ⎜ ρ ⋅ 1 ⎟ : ⎜ ρ ⋅ 2 ⎟ = l1 : l2
⎝ S⎠ ⎝ S⎠
Rx : Rm = l1 : l2
Rx = Rn ⋅
l1
l2
Tabella delle misure
Rm = 50 + 20 = 70Ω Er =1%(costruttore)
Ripetere le misure più volte ed usare il valore medio e calcolare l’errore assoluto.
Rn±Ea
L1±Ea
L1±Ea
Rn±Ea
(cm)
(cm)
(Ω)
(Ω)
70,0±0,7 89,8±0,5 60,2±0,5 104±2
1%
0,6%
0,8%
2%
24
Trasformazione di energia elettrica in meccanica.
Effetto joule.
Strumenti e apparecchiature utilizzati.
-
Generatore di tensione continua, con potenziometro per prelevare una tensione variabile(∆VCB)
220V in ingresso, 0 ÷12V in uscita.
Tester usato come voltmetro con cavetti e puntali:
Portata utilizzata = 10V,2V
Numero di divisioni = 50div
Sensibilità = 0,2V/div;0,04V/div
Classe = 1,5
Amperometro a zero centrale con più portate:
Portata utilizzata = 1,5A;0,3A
Numero di divisioni = 30
Sensibilità =0,05A/div; 0,01A/div
Classe = 1,5
Calorimetro con agitatore Ccal=40J/K.
-
Termometro a mercurio con sensibilità 0.1° centigrado.
-
Cronometro con sensibilità do 0.01 secondo.
-
-
-
25
-
Resistenza elettrica di 10Ω
-
Provetta graduata con sensibilità 1ml
-
Acqua deionizzata.
-
Tre cavetti di collegamento.
Come procedere:
a)
Si suddividono gli studenti in gruppi.
b)
Esegui il montaggio delle apparecchiature come da schema.(breve controllata alle
apparecchiature e ai collegamenti eseguiti dai gruppi di studenti.)
c)
Si prelevano 200ml di acqua con una provetta si determina la massa ricordando la densità
dell’acqua distillata.
d)
Si versa l’acqua nel calorimetro misurando la temperatura iniziale T1 .
e)
Supponiamo di non essere in passaggi di stato e di considerare trascurabili le perdite termiche
del calorimetro.
f)
Si aziona l’alimentatore con a tensione di 8V
g)
Si leggono gli strumenti e si lascia trascorrere 300 secondi agitando delicatamente e
costantemente il calorimetro.
h)
Trascorsi i 300 secondi si legge la temperatura finale T2 .
i)
Trascorsi altri 300 secondi si legge nuovamente la temperatura finale T2 .
j)
Si ripete questa operazione per altre due volte.
26
T1°C
m(Kg)
Er
Er
(0,200±0,003)
0,015
(0,200±0,003)
0,015
(0,200±0,003)
0,015
(0,200±0,003)
0,015
∆V(V)
Er
∆t(s)
Er
Er
(300,00±0,01)
(600,00±0,01)
(900,00±0,01)
(1200,00±0,01)
I(A)
Er
∆T=T2-T1°C
T2°C
Er
∆V ·I·∆t
Er
m·∆T
Er
Ccal·∆T
Er
∆V ·I·∆t- Ccal·∆T
Er
Costruire il grafico con carta millimetrata posizionando sull’asse x il prodotto della massa per la
variazione di Temperatura e sull’asse y il lavoro compiuto dall’energia elettrica meno la quantità di
calore assorbita dal calorimetro e tracciare la retta che meglio si avvicina a tutti i punti..
1) Come risulta il rapporto fra il prodotto della massa per la variazione di Temperatura e il lavoro
compiuto dall’energia elettrica, entro i limiti del suo errore assoluto?
2) Cosa rappresenta la pendenza della retta con questa scelta degli assi cartesiani.
3) Quale legge di proporzionalità lega le due grandezze variabili?
4) Calcolare dal grafico la pendenza della retta usando due punti della retta.
27
Esercizi inerenti alle esperienze di laboratorio.
Prove di valutazione.
a) Un filo di alluminio lungo 49 m e di diametro 0,70 mm è collegato in serie con un filo di rame
lungo 98 m e avente lo stesso diametro. L'intensità di corrente che attraversa i fili è 1 A.
Calcolare su ogni filo la caduta di tensione e l'intensità del campo elettrico.
[11,2 V; 13,6 V; 0,23 V/m; 0,14 V/m]
b) Confrontare i risultati della tabella con quelli calcolati in laboratori.
c) Il campo elettrico in un filo di rame percorso dalla corrente di 2 A è 5 • 10-3 V/m. Calcolare il
diametro del filo.
[2,9 mm]
d) Una bobina è formata da 500 spire (figura qui sotto) di filo di acciaio di sezione 0,4 mm2. Il
diametro delle spire è 4 cm. Calcolare la resistenza della bobina.
[28,3Ω]
e) Una bobina è costituita da 1000 spire circolari di diametro 10 cm. Sapendo che il filo
conduttore ha una sezione di raggio 0,2 mm e resistività 10-8 Ω m, determinare la d.d.p. da
applicare agli estremi del filo affinché la bobina sia percorsa dalla corrente di 1 A. [25 V]
28
f) In un conduttore di resistenza 50Ω, immerso in un recipiente che contiene 2kg di acqua
distillata, passa una corrente di 0,4° per mezz’ora. Se idealmente nel recipiente non ci sono
perdite di calore, l’aumento della temperatura dell’acqua è?
[3,44°C]
g) Un filo conduttore è tagliato in parti uguali, ognuna delle quali viene riunita in un sistema in
parallelo. Calcolare il numero di parti, sapendo che la resistenza del filo è 150Ω e che la
resistenza equivalente è 6Ω.
[5]
h) Il circuito della figura è costituito da un sistema di tre resistenze da 4Ω, 4Ω, 6Ω, alimentato da
un generatore da 6 V con resistenza interna trascurabile. Calcolare l'intensità di corrente che
percorre il circuito, ed chiarire il funzionamento delle varie parti del circuito ed indicare il verso
della corrente nel circuito.
4Ω
[4 A]
4Ω
6Ω
6V
i) Nove fili di rame di lunghezza l e diametro d sono collegati in parallelo a formare un singolo
conduttore composto di resistenza R. Quale dovrebbe essere il diametro D di un singolo filo di
rame di lunghezza l per avere la stessa resistenza del conduttore composto?
29
j) Il circuito della figura, alimentato da un generatore di resistenza interna trascurabile, è percorso
da una corrente di intensità uguale a 1 A. Calcolare la resistenza indicata con x in figura, e
[2 Ω]
spiegare le varie parti del circuito
25 Ω
XΩ
100 Ω
22 V
k) In un circuito è inserita una resistenza da 9,6 0 e due generatori collegati in serie tra loro e aventi f.e.m. uguale a 5 V e uguale resistenza interna. L'intensità di corrente è 1 A. Calcolare la
resistenza interna dei generatori, ed realizzare uno schema del circuito.
30
[0,4 Ω]