1
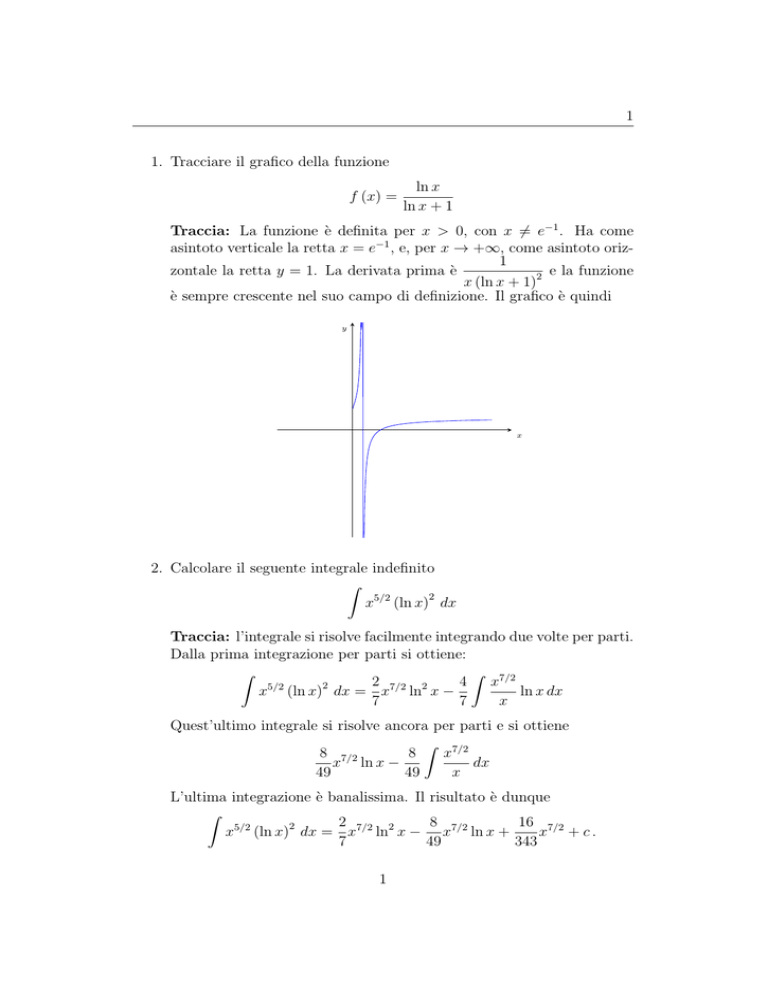
1. Tracciare il grafico della funzione
f (x) =
ln x
ln x + 1
Traccia: La funzione è definita per x > 0, con x 6= e−1 . Ha come
asintoto verticale la retta x = e−1 , e, per x → +∞, come asintoto oriz1
zontale la retta y = 1. La derivata prima è
e la funzione
x (ln x + 1)2
è sempre crescente nel suo campo di definizione. Il grafico è quindi
y
x
2. Calcolare il seguente integrale indefinito
Z
x5/2 (ln x)2 dx
Traccia: l’integrale si risolve facilmente integrando due volte per parti.
Dalla prima integrazione per parti si ottiene:
Z
Z 7/2
4
x
2 7/2 2
2
5/2
ln x dx
x (ln x) dx = x ln x −
7
7
x
Quest’ultimo integrale si risolve ancora per parti e si ottiene
Z 7/2
8 7/2
8
x
x ln x −
dx
49
49
x
L’ultima integrazione è banalissima. Il risultato è dunque
Z
2
8
16 7/2
x5/2 (ln x)2 dx = x7/2 ln2 x − x7/2 ln x +
x + c.
7
49
343
1
2
3. Studiare la convergenza semplice e assoluta della serie
+∞
X
n+2
n=1
n
2n x2n+1
Traccia: è una serie di potenze centrata nell’origine. Consideriamo la
serie dei moduli:
+∞
+∞ X
n + 2 n 2n+1 X
n + 2 n 2n+1 =
2 x
n 2 x
n
n=1
n=1
Applicando il criterio del rapporto, si ottiene
n + 3 n+1 2n+3 n −n −2n−1 n2 + 3n
n→+∞
2
x
2
x
=2 2
|x|2 −→ 2|x|2
n+1
n+2
n + 3n + 2
Quindi possiamo concludere che la serie converge semplicemente per
1
1
1
− √ < x < √ . In x = ± √ si ha una serie divergente.
2
2
2
4. Calcolare l’area della regione del piano compresa tra y = −ex e la retta
per A = (1, −e) e B = (0, −1).
Traccia: la retta per A e B ha equazione y = (1 − e)x − 1. Il grafico
delle curve è:
y
x
Per calcolare l’area bisogna risolvere l’integrale generalizzato seguente
Z +∞
|e−x − [(1 − e) x − 1] | dx
−∞
2
3
5. Studiare la funzione
f (x) = ex 1 − |2x − x2 |
Traccia: la funzione è definita su tutto R. Dobbiamo quindi studiare
x
e (1 − 2x + x2 ) , 0 ≤ x ≥ 2
f (x) =
x
e (1 − x2 + 2x) , x < 0, x > 2
La funzione ha come asintoto orizzontale l’asse delle ascisse. Quando
x → +∞ la funzione tende√a −∞. Inoltre, dallo studio della derivata
prima, si trova che x = − 3 e x = 1 sono punti di minimo, mentre
(controllando i limiti per x → 2 della f 0 (x)) si trova che x = 2 è un
punto di massimo. Il grafico è
y
x
6. Calcolare l’integrale
xex
dx
9 − ex
Traccia: ci sono vari modi per risolverlo. Uno di questi consiste nel
notare prima di tutto che ex (9 − ex )−1/2 è nella forma g 0 (x) ∗ f (g(x)).
Cosı̀, procedendo per parti si ottiene
Z
√
√
x
−2x 9 − e + 2
9 − ex dx
Z
√
Per risolvere quest’ultimo integrale, è consigliabile procedere con la
√
−2t
sostituzione t = 9 − ex da cui si ottiene dx =
dt. L’integrale
9 − t2
3
4
da risolvere è dunque
Z
Z
Z
Z
−t2
−t2 + 9 − 9
dt
4
dt = 4
dt = 4 dt − 36
= 4t−
2
2
9−t
9−t
9 − t2
1
√
x
√
9
−
e
36
−1
3
3
2 dt = 4 9 − ex − 12 tanh
9
3
t
1−
3
da cui segue la primitiva
√
√
√
9 − ex
−1
x
x
−2x 9 − e + 4 9 − e − 12 tanh
.
3
Z
7. Studiare la convergenza semplice e assoluta al variare di x reale della
serie
+∞
X
n
(−1)n
22n−1 x2n+1
(n
+
1)
(n
+
2)
n=0
Traccia: per la convergenza assoluta, usiamo il criterio del rappor2
to trovando,
al limite per n → +∞, 4|x | < 1. Quindi si trova
1 1
x∈ − ,
. In questo intervallo si ha convergenza assoluta (quindi
2 2
semplice). La serie converge anche negli estremi di questo intervallo
1
(verificare sostituendo x = ± nella serie di partenza).
2
8. Calcolare l’area della regione di piano compresa tra la curva y =
(x − 1) ln (x2 + 4) e l’asse delle x, per x ∈ [0, 1].
Traccia: il grafico del dominio è
y
x
4
5
Notiamo, con un banale calcolo, che x = 1 è l’intersezione della curva
con l’asse delle x, quindi l’integrale da calcolare (per parti) è
Z 1
(x − 1) ln(x2 + 4) dx .
0
9. Calcolare il limite seguente
1
x sin
+1
x3
lim
x→0
ln2 (1 + x2 )
5
10. Studiare la funzione
f (x) =
|ex − 2|
2ex − 1
11. Studiare la funzione
f (x) =
|x2 − 1| + |x|
x2 − 3x
5











