Resistori in serie e in parallelo

04_P109-129_schede(26-31)
17-05-2011
16:38
Pagina 121
Scheda
Resistori in serie e in parallelo
PREREQUISITI
Per affrontare la prova devi sapere:
쮿 Significato, definizione e unità di misura di:
– intensità di corrente elettrica
– differenza di potenziale
– resistenza elettrica
쮿 Come si utilizzano l’amperometro e il voltmetro
쮿 Come si calcola la resistenza equivalente
쮿 Che cosa significa collegamento in serie e in paral-
nel caso di collegamenti in serie e in parallelo di resistori
lelo di componenti elettrici
1 Titolo
Il titolo di questa prova, che prende in esame due possibili verifiche, può essere: Resistenze in serie e
in parallelo.
2 Obiettivi
La finalità dell’esperienza di laboratorio consiste nel valutare la validità delle formule che forniscono la
resistenza equivalente relativa a resistori collegati fra loro in serie oppure in parallelo.
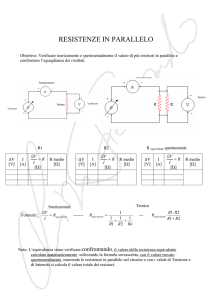
3a Schema e/o disegno
Nella figura 1 sono riportati gli schemi elettrici delle due situazioni che vogliamo studiare. (Ormai
dovrebbe essere chiaro come questi si traducano in circuiti elettrici reali.)
3b Materiale e strumenti
Il materiale utilizzato è:
• resistori (almeno due);
• cavi di collegamento;
• generatore;
• amperometro;
• voltmetro.
Figura 1
+ V −
+ V −
R1
a)
−
A
+
R1
R2
b)
+ G −
resistenze
in serie
−
A
+
R2
+ G −
resistenze
in parallello
04_P109-129_schede(26-31)
17-05-2011
16:38
Pagina 122
4 Contenuti teorici
Devi esporre concisamente che cosa si intende per collegamento in serie e in parallelo e quali sono le
regole per determinare la resistenza equivalente che corrisponde a un gruppo di resistori connessi fra
loro secondo le due modalità.
5 Descrizione della prova
Dal punto di vista esecutivo, la prova non dovrebbe presentare particolari difficoltà, in quanto le operazioni sono le stesse che hai già effettuato nelle esperienze precedenti, in particolare quella sulla verifica
della prima legge di Ohm. E del resto, il fatto di avere più resistenze in serie, ovvero più resistenze in
parallelo, non corrisponde a una reale novità, nel senso che hai già appreso a collegare in tale maniera i
due strumenti di misura: l’amperometro, che va disposto in serie nel circuito, e il voltmetro, che invece
deve essere messo in parallelo con il resistore ai capi del quale si vuole misurare la d.d.p.
Analogamente, rimangono le stesse anche le raccomandazioni relative alla prudenza con cui vanno eseguite le varie misurazioni.
Procedi preventivamente alla misurazione delle resistenze R1 ed R2 (qui ne immaginiamo due), anche se
probabilmente sui resistori è indicato il valore nominale del costruttore. Per fare questo, utilizzerai il circuito illustrato nella Scheda della prima legge di Ohm, semplificando però la procedura a una sola
misurazione per ciascuna resistenza. Supponiamo che i valori in questione siano quelli riportati nelle
colonne 1 e 3 delle righe corrispondenti a R1 ed R2 della tabella 1, alla pagina seguente.
Dopodiché, collega i due componenti in serie, rilevando il valore della corrente che li attraversa e la
d.d.p. ai capi della serie. Quindi, disponili in parallelo e, di nuovo, effettua la misurazione sia dell’intensità di corrente elettrica sia della differenza di potenziale. Come puoi vedere dalla tabella 1, noi abbiamo
preferito imporre ogni volta il medesimo valore della tensione ΔV.
In sintesi, le istruzioni sono le seguenti.
Parte I: resistenze in serie
a) Monta il circuito (ma senza effettuare ancora il collegamento con il generatore), seguendo lo schema
elettrico di figura 1a.
Ti facciamo notare che l’uscita del primo resistore devi collegarla con un cavetto all’ingresso del
secondo e che il voltmetro devi metterlo in parallelo con l’insieme dei due elementi, vale a dire:
l’ingresso (+) dello strumento è collegato con l’ingresso di R1, mentre la sua uscita è connessa con
l’uscita di R2, la quale va al polo negativo del generatore.
b) Alimenta il circuito con il generatore fino a raggiungere nel voltmetro il valore della d.d.p. desiderato, riportandolo con la rispettiva incertezza nelle colonne 1 e 2 della penultima riga, quella con Re
(serie), in tabella 1.
c) Leggi sull’amperometro il valore dell’intensità di corrente e la sua incertezza, inserendoli nelle colonne 3 e 4 della stessa riga della tabella.
d) Apri il circuito.
Questa parte è conclusa.
Parte II: resistenze in parallelo
a) Completa il circuito (ma senza effettuare ancora il collegamento con il generatore), seguendo lo schema elettrico di figura 1b.
Questa volta bisogna che colleghi fra loro gli ingressi dei due resistori, così come le rispettive uscite.
Il voltmetro, di conseguenza, è in parallelo sia con R1 sia con R2.
b) Alimenta il circuito con il generatore fino a raggiungere nel voltmetro il valore della d.d.p. desiderato, riportandolo con la corrispondente incertezza nelle colonne 1 e 2 dell’ultima riga, quella con Re
(parallelo), in tabella 1.
04_P109-129_schede(26-31)
17-05-2011
16:38
Pagina 123
c) Leggi sull’amperometro il valore dell’intensità di corrente e la sua incertezza, inserendoli nelle colonne 3 e 4 della stessa riga della tabella.
d) Apri il circuito.
In questo modo la fase operativa è terminata.
6 Raccolta dei dati
La tabella che segue riassume le misure delle resistenze dei singoli resistori e, quindi, quelle relative al
loro collegamento dapprima in serie e poi in parallelo.
I valori riguardano dei dati campione.
Tabella 1
1
DV
(V)
2
D x(DV )
(V)
3
I
(A)
4
Dx(I)
(A)
5
R = DV/I
(W)
6
D x(R)
(W)
R1
2,50
0,05
0,155
0,005
16,1
0,9
R2
2,50
0,05
0,110
0,005
23
2
Re (serie)
2,50
0,05
0,065
0,005
38
4
Re (parallelo)
2,50
0,05
0,240
0,005
10,4
0,5
letture
resistenze
7 Elaborazione
Con Re indichiamo la resistenza equivalente sperimentale, mentre quella teorica, che ricaveremo con il
calcolo a partire da R1 ed R2, la indichiamo con ReT.
Valori sperimentali
Utilizzando la prima legge di Ohm, puoi ottenere i valori delle resistenze riportate nella colonna 5 della
tabella 1:
R1 =
2,50
ΔV
=
= 16,12903 ≅ 16,1 Ω
0,155
I
e così via…
(Il procedimento per individuare le incertezze della colonna 6 lo trovi nell’help 1.)
Valori teorici
A partire dai dati presenti in tabella 1 delle due resistenze R1 ed R2, devi calcolare i valori teorici (cioè
determinati in base alle formule) delle resistenze equivalenti sia per la serie sia per il parallelo:
serie
ReT = R1 + R2 = 16,1 + 23 = 39,1 ≅ 39 Ω
parallelo ReT =
16,1 ⋅ 23
R1 ⋅ R2
=
= 9, 47059 ≅ 9 Ω
R1 + R2 16,1 + 23
(Per determinare le incertezze, se ti vengono richieste, puoi fare riferimento all’help 2 per la serie e all’help 3
per il parallelo.)
04_P109-129_schede(26-31)
17-05-2011
16:38
Pagina 124
8 Analisi dei risultati e conclusioni
A questo punto, puoi confrontare i risultati sperimentali con quelli teorici, giudicandoli soddisfacenti o
meno in base alla loro vicinanza, oppure, se hai calcolato le incertezze, sulla base della compatibilità
degli intervalli di indeterminazione (come illustrato in figura 2).
34
Re
ReT
38
36
42
39
42
Ω
Re
Ω
ReT
a)
9,9 10,4 10,9
Ω
7
9
11
Ω
b)
Figura 2 a) Confronto fra Re ed ReT nel collegamento in serie; b) confronto fra Re ed ReT nel collegamento in parallelo.
Un eventuale riscontro negativo può essere imputato, per esempio, a:
• instabilità nell’alimentazione elettrica;
• riscaldamento dei componenti;
• contatti non ottimali ecc.
help 1
Trattandosi di un rapporto, si moltiplica la somma degli errori relativi di ΔV e I per il valore di R:
⎡ Δx( ΔV ) Δx( I ) ⎤
5⎤
⎡ 0, 05 0, 005
+
⋅R=⎢
+
⎥
⎥⎦ ⋅ 16,12903 = 0,84290 ≅ 0, 9 Ω
Δ
0
,
155
V
I
2
,
50
⎣
⎣
⎦
Δx( R) = ⎢
help 2
Nel caso della somma, puoi trovare direttamente l’incertezza:
Δx(ReT) = Δx(R1) + Δx(R2) = 0,9 + 2 = 2,9 ≅ 3 Ω
help 3
Se in precedenza hai applicato più volte le leggi di propagazione degli errori, allora il seguente calcolo dovrebbe risultarti comprensibile:
0, 9 + 2 ⎤
⎡ Δx( R1 ) Δx( R2 ) Δx( R1 ) + Δx( R2 ) ⎤
⎡ 0, 9
2
+
+
⎥ ⋅ ReT = ⎢16,1 + 23 + 16,1 + 23 ⎥ ⋅ 9, 47059 = 2, 05540 ≅ 2 Ω
R
R
R
+
R
2
1
2
1
⎣
⎦
⎣
⎦
Δx( ReT ) = ⎢