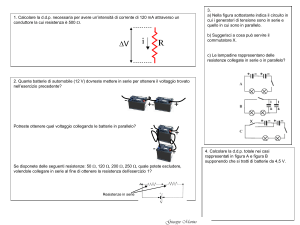
Problema n°1
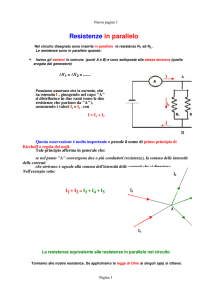
Sulla risoluzione di circuiti applicando i principi di Kirchhoff
primo principio di Kirchhoff "principio dei nodi " - la sommatoria di tutte le correnti che confluiscono in
un nodo (siano esse entranti o uscenti, prese con segno positivo se entranti e con segno negativo se
uscenti) deve essere nulla:
secondo principio di Kirchhoff "principio delle maglie" - la sommatoria di tutte le d.d.p. di ciascuna
maglia chiusa (siano esse entranti o uscenti, prese con segno positivo se entranti e con segno negativo se
uscenti) deve essere nulla:
per i generatori percorsi da - a +
per le resistenze percorse nello stesso verso della corrente ivi passante
per i condensatori percorsi dall'armatura positiva a quella negativa
L'esempio riportato, riassume molto bene il procedimento da seguire per risolvere un circuito applicando i
principi di Kirchhoff.
Problema n°2 (da svolgere applicando i principi di Kirchhoff)
Considera il circuito in figura. Determina le intensità e i versi delle correnti che circolano nei tre resistori.
(
)
Problema n°3
Nel circuito di figura tutte i tre resistori hanno resistenze uguali e valgono 20 . Il generatore fornisce una
fem di 16,0 V.
a) quali valori segnano l'amperometro A e il voltmetro V?
b) qual è la potenza fornita dall'alimentatore?
R = 20
= 16,0 V
resistenze
fem del generatore
Si determina, dapprima, la resistenza equivalente della serie:
Poi quella totale (dal parallelo):
La corrente che circola nel circuito equivalente e che è quella misurata dall'amperometro, sarà:
Per determinare la tensione misurata dal voltmetro, devo calcolare la corrente che circola nella resistenza;
ossia devo calcolare come la corrente I di 1,2 A (calcolata) si distribuisce nei due rami del parallelo. Se
chiamo I1 la corrente che circola nel ramo con una sola resistenza e I2 quella che circola nell'altro ramo,
considerando che tutti i rami di un parallelo sono sottoposti alla stessa tensione, posso scrivere, applicando
la I legge di Ohm:
Quindi, per l'equilibrio nel nodo da cui si dipartono i rami del parallelo:
Le due resistenze uguali, poste nel secondo ramo del parallelo sono entrambe sottoposte alla stessa
corrente I2; quindi, la tensione misurata dal voltmetro sulla prima resistenza (che, per ovvi motivi sarà uguale
a quella sulla seconda resistenza) è:
Valore questo, pari alla metà della fem della batteria; d'altronde, la V cui è sottoposto il ramo con due
resistenze, uguale alla fem, viene "consumata" da due resistori di identica resistenza, per cui ognuna sarà
sottoposta alla metà della fem stessa!!!!!!
La potenza fornita dall'alimentatore è determinabile considerando il circuito semplificato con il resistore
"equivalente" in sostituzione delle resistenze realmente presenti; per cui:
Problema n°4
In un collegamento a Internet senza fibra ottica, il segnale della rete passa attraverso un doppino telefonico,
ossia una coppia di cavi in rame del diametro ognuno di circa 10-3 m. A causa della piccola corrente che vi
scorre, questi cavi producono un calore praticamente nullo e quindi sono alla temperatura ambientale.
Tipicamente tra la centralina e un appartamento ci sono 50 m di cavo telefonico. Considera una temperatura
invernale di -3 °C e una estiva di 32 °C.
Determinare la variazione relativa di resistenza tra inverno ed estate.
d = 10-3 m
diametro del cavo di rame
l = 50 m
lunghezza del cavo di rame
t1 = -3 °C
T1 = -3+273,15 K = 270,15
temperatura invernale
temperatura invernale espressa in kelvin
T2 = 32 °C
T2 = 32+273,15 K = 305,15
temperatura estiva
temperatura estiva espressa in kelvin
Per risolvere questo problema bisogna considerare la variabilità della resistività con la temperatura,
secondo la relazione:
dove è la resistività alla temperatura T (misurata in gradi Kelvin),
il valore della resistività misurato a
293 K (circa 20 °C), un parametro caratteristico di ogni materiale e T la differenza di temperatura tra T,
espressa in K e la temperatura di riferimento ( 293 K ).
Per il rame si ha:
m
Per cui, si ha:
Per determinare la variazione relativa tra inverno ed estate si rapportano i valori di R ed R1