Ordinario 2005

ESAMI DI STATO A.S. 2004-05
LICEO SCIENTIFICO – Corso di ordinamento
Risoluzione utilizzando Derive e Cabri.
Problema N. 1
Nel primo quadrante del sistema di riferimento Oxy, ortogonale e monometrico, si consideri
la
regione R, finita, delimitata dagli assi coordinati e dalla parabola λ d’equazione: y = 6 – x2 .
1.
Si calcoli il volume del solido generato dalla rotazione completa di R attorno all’asse y.
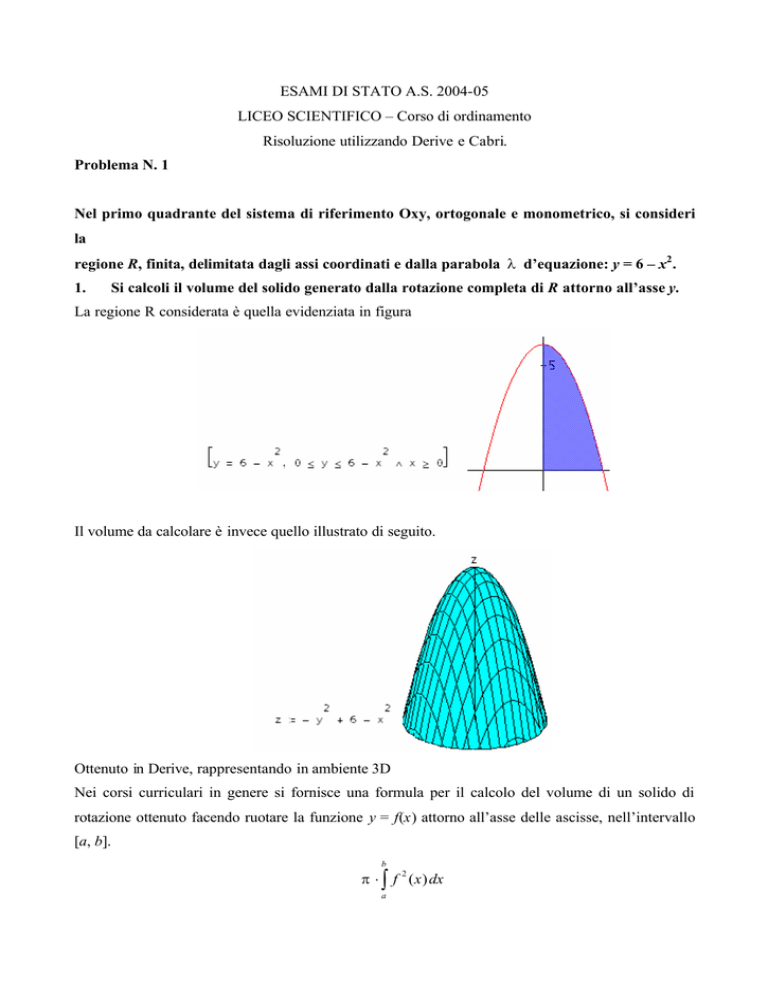
La regione R considerata è quella evidenziata in figura
Il volume da calcolare è invece quello illustrato di seguito.
Ottenuto in Derive, rappresentando in ambiente 3D
Nei corsi curriculari in genere si fornisce una formula per il calcolo del volume di un solido di
rotazione ottenuto facendo ruotare la funzione y = f(x) attorno all’asse delle ascisse, nell’intervallo
[a, b].
b
π ⋅ ∫ f 2 ( x ) dx
a
In questo caso abbiamo a che fare invece con la rotazione attorno all’asse delle ordinate. In questo
caso quindi è opportuno considerare la simmetrica della parabola rispetto alla prima bisettrice degli
assi, ossia la curva di equazione x = 6 – y2 .
In questo caso perciò il volume sarà pari a
2.
Si calcoli il volume del solido generato dalla rotazione completa di R attorno alla retta y
= 6.
Ruotando attorno alla retta
y = 6, che è tangente alla parabola nel suo vertice, avremo il
ribaltamento della regione come mostrato in figura.
Basta quindi traslare la parabola in modo tale che la retta y = 6 divenga la retta y = 0 e applicare le
formule viste.
Anche se non corretta, può accettarsi (con un punteggio inferiore) la soluzione, data da alcuni (per
esempio il Corriere della Sera) in cui si calcola il volume della parte “vuota”, cioè la differenza fra
il cilindro di raggio 6 e altezza
3.
6 e il precedente volume, ossia:
Si determini il valore di k per cui la retta y = k dimezza l’area di R.
Dobbiamo stabilire per quale k le due aree evidenziate sono uguali
Naturalmente poi, in ambiente 2D, dobbiamo inserire la slider bar dipendente dal parametro h,
diversamente si ottiene messaggio di errore.
Cominciamo a determinare l’ascissa positiva dell’intersezione fra l’arco di parabola e la retta.
Naturalmente scegliamo solo uno dei due rami, per esempio quello positivo. Quindi la condizione
richiesta equivale alla seguente equazione:
dato che nel primo caso determiniamo l’area come differenza fra l’area sottesa dall’arco di parabola
e l’area del rettangolo di dimensioni pari alle coordinate del punto intersezione.
4.
Per 0 < t < 6 sia A(t) l’area del triangolo delimi tato dagli assi e dalla tangente a ? nel
suo punto di ascissa t. Si determini A(1).
L’equazione della generica tangente all’arco di parabola in un suo punto di ascissa t è
le sue intersezioni con gli assi coordinati sono:
Il triangolo di cui si deve calcolare l’area è quello in figura
e la sua area è ovviamente
.
5.
Si determini il valore di t per il quale A(t) è minima.
In generale invece l’area è
Il cui minimo è
Abbiamo verifichiamo che effettivamente è un minimo.
Problema N. 2
Si consideri la funzione f definita sull’intervallo 0;+∞ da:
 f (0) = 1

2
 f ( x ) = 1 / 2 x [3 − 2 log( x) ] + 1 se x > 0
e sia C la sua curva rappresentativa nel riferimento Oxy, ortogonale e monometrico.
1.
Si stabilisca se f è continua e derivabile in 0.
La funzione è la seguente
Verifichiamo la continuità, come si nota dal grafico.
Passiamo alla derivabilità.
La funzione è anche derivabile a destra per x = 0 e la sua derivata è 0.
2.
Si dimostri che l’equazione f(x) = 0 ha, sull’intervallo 0;+∞ un’unica radice reale.
Tenuto conto del grafico precedente possiamo confermare quanto richiesto. In ogni caso possiamo
usare il calcolo differenziale.
Abbiamo verificato che per x = e vi è un massimo relativo. Ma dato che la funzione cresce per x < e,
e il suo minimo valore è x = 1, mentre decresce per x > e, può tagliare al massimo in un punto l’asse
delle ascisse. Anzi, visto che
lo taglia esattamente in un punto.
Volendo possiamo determinare anche un valore approssimato della radice.
La radice è quindi pari a circa 4.69. Confermiamo con Derive
3.
Si disegni C e si determini l’equazione della retta r tangente a C nel punto di ascissa x =
1.
Possiamo disegnare la curva con ciò che abbiamo già trovato, dato che l’I.d.E. è [0, +∞[, la
funzione non ha asintoti verticali, né di altro tipo; abbiamo anche determinato crescenza e
decrescenza e il punto di massimo.
Troviamo l’equazione della tangente.
4.
Sia n un intero naturale non nullo. Si esprima, in funzione di n, l’area An del dominio
piano delimitato dalla curva C, dalla retta tangente r e dalle due rette: x =
Consideriamo che tipo di punto è quello per cui x = 1.
1
e x = 1.
n
Quindi abbiamo un flesso ascendente. Ciò significa che per x < 1 la tangente sta sotto la curva,
quindi la regione di cui si vuole calcolare l’area è quella in figura
La cui area è
5.
Si calcoli il limite per n → +∞ di An e si interpreti il risultato ottenuto.
Il limite da calcolare è
Ovviamente per n che tende all’infinito la retta di equazione x = 1/n diventa l’asse delle ordinate, e
l’area da calcolare è quella in figura.
Questionario
1.
Si dimostri che il lato del decagono regolare inscritto in un cerchio è sezione aurea del
raggio e si utilizzi il risultato per calcolare sen18°, sen36°.
Si dice che un segmento è parte aurea di un altro se il primo è medio proporzionale fra l’altro
segmento e la differenza di questo dal primo. Ciò significa che la sua misura x, detta l la misura del
segmento maggiore, verifica l’equazione
l: x = x: l − x ⇒ x 2 = l ⋅ ( l − x ) ⇒ x 2 + lx − l 2 = 0 ⇒ x = l ⋅
−1 ± 5
−1 + 5
⇒ x = l⋅
2
2
abbiamo escluso ovviamente la soluzione negativa.
Ora, come si vede in figura, il lato del decagono regolare è tale da essere base di un triangolo
isoscele in cui i lati obliqui misurano quanto i raggi del cerchio circoscritto. Con Cabri otteniamo la
seguente figura
Tracciamo la bisettrice di uno degli angoli alla base, dividendo il triangolo in due triangoli, uno dei
quali, ABC in figura, è simile a quello di partenza AOB.
Vale allora la seguente proporzione:
2
2
AO: AB = AB: AC ⇒ AB = AO ⋅ AC ⇒ AB = AO ⋅ ( AO − OC) ⇒
2
2
⇒ AB = AO ⋅ ( AO − BC) ⇒ AB = AO ⋅ ( AO − AB)
cioè quanto voleva provarsi, il che vuol dire che
AB −1 + 5
=
2
AO
Applicando adesso il teorema dei seni ad ABC avremo
AB = 2 ⋅ AO ⋅ sin(18° ) ⇒ sin(18° ) =
1 AB 1 5 − 1
5 −1
⋅
= ⋅
=
2 AO 2
2
4
Infine
2
5 −1
( 5 − 1)
sin( 36° ) = 2 ⋅ sin(18° ) ⋅ cos(18° ) = 2 ⋅ sin(18° ) ⋅ 1 − sin (18° ) = 2 ⋅
⋅ 1−
=
4
42
2
=
5 −1
6− 2⋅ 5
5 −1 8− 3+ 5
⋅ 1−
=
⋅
=
2
16
2
8
5 −1 5 + 5
⋅
=
2
8
3 − 5 5+ 5
10 − 2 ⋅ 5
⋅
=
2
8
4
Più semplicemente con Derive avremmo avuto:
2.
Una bevanda viene venduta in lattine, ovvero contenitori a forma di cilindro circolare
retto, realizzati con fogli di latta. Se una lattina ha la capacità di 0,4 litri, quali devono
essere le sue dimensioni in centimetri, affinché sia minima la quantità di materiale
necessario per realizzarla? (Si trascuri lo spessore della latta).
Il cilindro si ottiene a partire da un rettangolo e da due cerchi, la cui superficie è 2πrh + 2πr2 .
Dobbiamo minimizzare questa funzione, che dipende da due variabili. Però le variabili r e h sono
legate fra loro mediante la formula del volume V = πr2 h. Quindi avremo, tenuto conto che 0,4 litri
sono 0,4 dm3 = 400 cm3
Pertanto la funzione da minimizzare, in funzione solo di r, è
Determiniamone il minimo
Adesso determiniamo il valore di h
3.
Si dimostri che la curva y = x sen x è tangente alla retta y = x quando sen x = 1 ed è
tangente alla retta y = -x quando sen x = -1.
Determiniamo le tangenti alla curva in un suo punto generico di ascissa x 0 .
Vediamo cosa accade quando
Vediamo cosa accade quando
Rappresentiamo graficamente
4.
Si dimostri che tra tutti i rettangoli di dato perimetro, quello di area massima è un
quadrato.
Dato un rettangolo di lati a e b e di perimetro noto 2p, avremo che la sua area è
Ricaviamo b mediante a.
Determiniamo il massimo:
Per questo valore il rettangolo diventa quadrato.
5.
Il numero e di Nepero [nome latinizzato dello scozzese John Napier (1550-1617)]: come
si definisce? Perché la derivata di ex è ex ?
+∞
1
x
= e . Per determinare la derivata di e , dobbiamo calcolare
n
!
n =0
Si ha: lim (1 + 1 / n) n = ∑
n →+∞
x − x0
y
e x − e xo
−1
x e
x e −1
lim
= lim e ⋅
= lim e ⋅
= ex
x → xo x − x
x→ x o
y
→
0
x − xo
y
o
6.
Come si definisce n! (n fattoriale) e quale ne è il significato nel calcolo combinatorio?
Quale è il suo legame con i coefficienti binomiali? Perché?
Si ha: n ! = 1 ⋅ 2⋅...⋅n, ∀n ∈ N . Nel calcolo combinatorio il fattoriale di un numero calcola il numero
n
di permutazioni di n oggetti distinti. I coefficienti binomiali   , che si trovano nel binomio di
k 
n
 n
Newton: (a + b ) n = ∑   ⋅ a n− k ⋅ b k , sono legati ai fattoriali dalla seguente relazione:
k =0  k 
7.
.
Se f(x) = x – 4x + 4x + 3 per quanti numeri reali k è f(k) = 2? Si illustri il ragionamento
4
3
2
seguito.
Con Derive possiamo seguire diversi percorsi.
Risolvere l’equazione
Rappresentare graficamente
Scrivere il polinomio in modo che sia evidentemente che è privo di zeri reali
Infine applicare il teorema di esistenza degli zeri
In ogni caso non ci sono soluzioni reali.
8.
I centri delle facce di un cubo sono i vertici di un ottaedro. E’ un ottaedro regolare?
Quale è il rapporto tra i volumi dei due solidi?
In Derive possiamo rappresentare la figura nel riferimento 3D, mediante i seguenti comandi
Gli spigoli sono tutti isometrici perché i triangoli ILM, ILK, IJK, IJM, NKJ, NJM, NLM, NLK sono
tutti isometrici. La misura si ottiene tenendo conto che nel triangolo rettangolo IPQ si ha:
IP =
l
, PQ = x , IQ = x ⋅ 3 , quindi
2
l2
l2
l
l
= x 2 + 3x2 ⇒ x2 =
⇒x=
⇒ JN = 2 ⋅ PQ = 2 x =
4
8
8
2
Il volume dell’ottaedro è il doppio del volume di una delle due piramidi che lo formano, la cui
altezza è metà del lato del cubo. Perciò il rapporto dei due volumi è
l3
2⋅
l2
l 1
⋅ ⋅
2 2 3
2
=
l3
=6
2
l l
2⋅ ⋅
2 6
9.
Si calcoli, senza l’aiuto della calcolatrice, il valore di: sen2 (35°) + sen2 (55°) ove le misure
degli angoli sono in gradi sessagesimali.
Abbiamo sen2 (35°) + sen2 (55°) = sen2 (35°) + cos2 (35°) = 1
10.
Si dimostri, calcolandone la derivata, che la funzione f ( x) = arctg x − arct
x−1
è
x+1
costante, indi si calcoli il valore di tale costante.
L’I.d.E. della funzione è x ≠ −1 .
Si ha:
Il problema però è che la funzione non è continua, quindi non derivabile per x = -1, quindi non è
costante dappertutto. Infatti
se x > −1
π / 4
Pertanto abbiamo f ( x ) = 
.
− 3 / 4π se x < −1