Applicazioni del primo principio della
termodinamica ed utilizzo delle tabelle del
vapore: Esercizi svolti
19 marzo 2013
Esercizio 1
Un recipiente di volume ssato e con pareti adiabatiche è diviso in due
parti da un setto non adiabatico. Una parte contiene 10 kg di acqua alla
temperatura di 20◦ C, l'altra, di massa pari a 2.5 kg, contiene acqua alla
temperatura di 80◦ C. Determinare la temperatura nale del sistema una volta
raggiunto l'equilibrio termico.
T1
T2
V1
V2
Figura 1.1:
Tf
Vf
Schema del sistema termodinamico in esame
Soluzione
Il sistema complessivo, formato dai due sotto-sistemi 1 e 2 divisi dal setto,
è un sistema isolato, in quanto le pareti, sse ed adiabatiche, non consentono
nè scambi di lavoro (L) nè di calore (Q). Inoltre la massa (m) del sistema è
costante e non subisce nè variazioni di quota (z ) nè di velocità (w). Per cui
complessivamente dall'applicazione del primo principio della termodinamica
si ha:
∆(w2 )
∆U = Q + L + mg∆z + m
=0
(1.1)
2
Si avrà quindi che
Q1 = ∆U1 = −Q2 = −∆U2
1
(1.2)
ricordando che il calore scambiato da un liquido è legato alla sua variazione
di temperatura dalla relazione Q = mc∆T dove si è fatto uso del calore
specico c, assunto costante con la temperatura, si ha
m1 c (T1 − Tf ) = −m2 c (T2 − Tf )
(1.3)
dove la temperatura nale dei due sottosistemi è la stessa poichè si trovano
in equilibrio termico.
Tf =
m1 T1 + m2 T2
= 32◦ C
m1 + m2
(1.4)
La temperatura di equilibrio risulta pari alla media pesata sulle masse dei due
sotto-sistemi, e quindi è più vicina alla temperatura del sistema con massa,
ovvero capacità termica maggiore.
Esercizio 2
Un sistema termodinamico chiuso formato da un cilindro ed un pistone
mobile (Fig. 2.1) esegue una trasformazione di espansione durante la quale
scambia 40 kJ di lavoro attraverso il pistone. Sapendo che la variazione di
energia interna è pari a 660 kJ, calcolare il calore scambiato da sistema.
L
11
00
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00000000
11111111
00
11
00000000
11111111
00000000
11111111
p
V
T
Q
U
Figura 2.1:
Schema del sistema cilindro-pistone
Soluzione
Applicando il primo principio per sistemi chiusi, e considerando nulle le
variazioni di quota e velocità del sistema si ottiene:
Q + L = ∆U =⇒ Q = ∆U − L = 660 kJ − (−40 kJ) = 700 kJ
2
(2.1)
Si osservi che, secondo la convenzione dei segni adottata, Q è positivo in
quanto entrante nel sistema (energia termica entrante sistema), mentre L
è negativo perchè eettuato dal sistema sull'ambiente (energia meccanica
uscente dal sistema).
Esercizio 3
Un contenitore termicamente isolato contiene inizialmente 130 g di acqua alla temperatura di 80◦ C ed un cubetto di ghiaccio di massa 12 g alla
temperatura di −10◦ C. Si calcoli la temperatura nale di equilibrio sapendo
che:
• calore specico dell'acqua è ca = 4.186 kJ/(kgK);
• calore specico del ghiaccio è cg = 2.220 kJ/(kgK);
• calore latente di fusione hl = 333 kJ/kg;
Soluzione
È possibile identicare tre sistemi termodinamici:
• ghiaccio. Scambia calore ma non lavoro con il suo ambiente;
• acqua. Scambia calore ma non lavoro con il suo ambiente;
• sistema complessivo formato dalla somma degli altri due sistemi. È un
sistema isolato.
Il sistema complessivo è, formato da acqua e ghiaccio non scambia nè calore
nè lavoro con l'ambiente (sistema isolato), quindi:
∆U = Q + L = 0
(3.1)
Il calore scambiato dall'acqua Qa sarà i opposto di quello scambiato dal
ghiaccio (Qg ).
Qg = −Qa
(3.2)
Il calore scambiato dal ghiaccio può essere scomposto in 3 contributi:
• riscaldamento dalla temperatura iniziale (T1g = −10◦ C) no alla
temperatura di fusione (Tl = 0◦ C)
Qg1 = mg cg (Tl − T1g ) = 0.2664 kJ
3
(3.3)
• calore latente di fusione. In questa fase il calore assorbito non causa
l'innalzamento della temperatura del sistema ma la progressiva fusione
del solido.
Qg2 = mg hl = 3.996 kJ
(3.4)
• Riscaldamento no alla temperatura di equilibrio Tf
Qg3 = mg ca (Tf − Tl )
(3.5)
Nel calcolo di Qg3 is è fatto uso del calore specico dell'acqua perchè
oramai il sistema è passato interamente allo stato liquido.
Il calore scambiato dal sistema termodinamico acqua è:
Qa = ma ca (Tf − T1a )
(3.6)
Q1g + Q2g + Q3g = −Qa
(3.7)
Dall'equazione (3.2)
Utilizzando le espressioni (3.5) e (3.6) si ottiene
Q1g + Q2g + mg cg (Tf − T1g ) = −ma ca (Tf − T1a )
(3.8)
Si osservi che la temperatura nale è comune ad entrambi i sistemi termodinamici considerati perchè i due sistemi si trovano in equilibrio termodinamico.
Sostituendo i valori di Q1g e Q2g , e risolvendo per Tf si ottiene:
Tf =
mg cg T1g + mg ca Tl − Q1g − Q2g
= 66◦ C
(ma + mg )ca
(3.9)
Esercizio 4
Dell'aria a temperatura T1 = 293 K e velocità w1 = 1 m/s attraversa un
condotto inclinato a sezione costante. La dierenza di quota tra la sezione di
ingresso e di uscita è di 10 m. All'uscita la temperatura dell'aria è di T2 =
40◦ C e la velocità è w2 = 3 m/s. Determinare la quantità di calore scambiata
(q) per unità di massa lungo il condotto, supponendo che non ci siano scambi
di lavoro. Si utilizzino le formule di Langen per il calcolo del calore specico
dell'aria (a = 992.082 J/kgK; a0 = 703.248 J/kgK; b = 0.134 J/kgK2 )
4
Soluzione
Dall'espressione del primo principio della termodinamica per sitemi aperti, ricordando che non si hanno scambi di lavoro, si ottiene:
q = h2 − h1 +
w2 − w1
+ g∆z
2
(4.1)
Considerando l'aria assimilabile ad un gas perfetto la variazione entalpica si
può valutare come:
h2 − h1 = cp 2 T2 − cp 1 T1
(4.2)
Si osservi che, avendo considerato l'aria come un gas perfetto (ma non ideale),
la funzione di stato entalpia, rimane funzione della sola temperatura del
gas, ma i calori specici non sono costanti lungo la trasformazione, bensì
dipendono dalla temperatura attraverso le formule di Langen cp = a + bT .
In particolare si ottiene:
cp 1 = 1031 J/(kgK)
cp 2 = 1034 J/(kgK)
(4.3)
Avendo avuto l'accortezza di convertire la temperatura di uscita in Kelvin
T2 = 40◦ C = 313 K. Sostituendo i valori nell'eq. (4.1) si ottiene:
q = 21567 J/kg
(4.4)
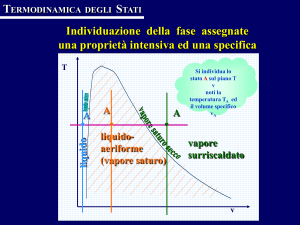
Esercizio 5
Un recipiente chiuso contiene una miscela di acqua allo stato liquido e
di vapore in condizioni di saturazione alla temperatura di 120◦ C. Sapendo
che il titolo è x = 0.85, si determinino pressione entalpia, entropia e densità
della miscela.
5
Soluzione
Figura 5.1:
Estratto delle tabelle del vapore saturo.
Dalle tabelle del vapore, di cui un estratto è riportato in Fig. 5.1, si
ottiene che la pressione di saturazione alla temperatura di 120◦ C è di 1.987
bar. La tabella in Fig. 5.1 riporta le principali grandezze di stato al variare
della temperatura per il liquido saturo e vapore saturo. Le proprietà della
miscela acqua/vapore in condizioni intermedie si calcolano per interpolazione
lineare utilizzando come variabile interpolante il titolo.
h(x) = xhv + (1 − x)hl = 0.85 · 2706 kJ/kg + (1 − 0.85) · 503 kJ/kg
(5.1)
= 2376 kJ/kg
analogamente per le altre grandezze:
s(x) = xsv + (1 − x)sl = 6.890 kJ/(kgK)
(5.2)
v(x) = vsv + (1 − x)vl = 0.758 m3 /kg
(5.3)
La densità si ricava come l'inverso del volume specico:
ρ=
1
= 1.32 kg/m3
v
(5.4)
Esercizio 6
Un recipiente contiene vapore alla pressione p = 25 bar ed alla temperatura T = 400◦ C; calcolare entalpia ed entropia speciche del sistema.
6
Soluzione
Figura 6.1:
Estratto delle tabelle del vapore saturo.
Dalle tabelle del vapore saturo, riportate in Fig. 6.1, si ricava che la
temperatura di saturazione del vapore a 25 bar è pari a Ts = 224◦ C. Essendo
T > Ts il uido si trova in condizioni di vapore surriscaldato. Pertanto è
necessario far riferimento alle tabelle dell'acqua/vapore surriscaldato, di cui
un estratto è riportato in Fig. 6.2.
Figura 6.2:
Estratto delle tabelle del vapore surriscaldato.
Nella tabella in Fig. 6.2 non sono presenti i dati relativi alla pressione
di 24 bar. È quindi necessario procedere all'interpolazione lineare tra le
pressioni di 24 bar (Punto A nel seguito) e 26 bar (Punto B nel seguito) ed
alla temperatura di 400◦ C. Utilizzando l'espressione della retta per due punti
7
abbiamo
h − hA
hB − hA
hB − hA
=
=⇒ h = hA +
(p − pA ) = 3240 kJ/kg (6.1)
p − pA
pB − p A
pB − pA
s − sA
sB − sA
sB − sA
=
=⇒ s = sA +
(p − pA ) = 7.0175 kJ/kgK (6.2)
p − pA
p B − pA
p B − pA
Esercizio 7
Una caldaia produce vapore alla pressione di 40 bar ed alla temperatura
di 300◦ C. Supponendo che il uido si trovo inizialmente alla temperatura di
60◦ C, tracciare le trasformazioni termodinamiche e calcolare il calore assorbito da 1 kg di acqua. Si trascuri lo scambio di calore verso l'esterno della
caldaia.
Soluzione
(a) diagramma entropico
Figura 7.1:
h − s.
(b) diagramma di Molliere
Rappresentazione delle trasformazioni sui diagrammi T − s ed
La temperatura iniziale del uido è minore della temperatura di saturazione alla pressione di 40 bar (Ts = 250.3◦ C). All'uscita dalla caldaia si
hanno condizioni di vapore surriscaldato poichè la temperatura, in questo
caso è maggiore della temperatura di saturazione. Pertanto la trasformazione
termodinamica seguita dal uido nella caldaia, rappresentata in Fig. 7.1, può
essere divisa in tre parti:
1-2 riscaldamento del liquido dalle condizioni iniziali no alla condizione di
liquido saturo. La trasformazione è una isobara, che risulta sostanzialmente coincidente con la curva limite inferiore nei diagrammi T − s ed
h − s;
8
2-3 vaporizzazione del liquido. In questa fase il calore assorbito dall'acqua viene interamente assorbito dal calore latente di vaporizzazione, di
conseguenza la temperatura rimarrà costante durante tutta la fase di
vaporizzazione. La trasformazione si dice isotermobarica ed è rappresentata dal tratto orizzontale (2-3) sul piano T − s, e dalla retta (2-3)
tangente alla curva limite inferiore sul piano h − s;
3-4 surriscaldamento del vapore saturo. Una volta terminata la fase di vaporizzazione la temperatura ricomincia ad aumentare lungo l'isoterma
di surriscaldamento (3-4).
Figura 7.2:
Estratto delle tabelle del vapore.
Il calore complessivamente assorbito dall'acqua può essere calcolato applicando il primo principio per sistemi aperti (q + l = ∆h), tra le condizioni
di ingresso ed uscita dalla caldaia. Ricordando che il lavoro scambiato è nullo (l = 0), ed utilizzando i dati di entalpia ricavati dalle tabelle del vapore
surriscaldato (Fig. 7.2) si ottiene
q = h4 − h1 = 2962 kJ/kg − 254 kJ/kg = 2707 kJ/kg
(7.1)
Si osservi che le tabelle del vapore generalmente riportano nella stessa tabella
i dati relativi sia al vapore surriscaldato (T > Tsat ) sia all'acqua liquida
(T < Tsat ), mentre i valori relativi al uido in transizione di fase sono tabellati
separatamente.
9
Esercizio 8
Un contenitore rigido e chiuso contiene 10 kg di acqua ed 1 kg di vapore
in condizioni di equilibrio alla pressione di p1 = 1 bar. Viene fornito calore
al sistema no al raggiungimento di una pressione p2 = 5 bar. Calcolare la
quantità di calore fornita al sistema ed il titolo del vapore nelle condizioni
iniziali e nali.
Soluzione
La trasformazione può essere ecacemente rappresentata nel piano termodinamico p − v come eettuato in Fig. 8.1, dove si può osservare che
l'aumento di pressione a volume costante porterà ad aumento del titolo della
miscela.
p
Curva limite inferiore
Curva Limite Superiore
Vapore saturo
p2
2
1
p1
v
Figura 8.1:
Rappresentazione della trasformazione sul piano p − v.
Il titolo nelle condizioni iniziali è pari al rapporto tra la massa di vapore
mv1 e quella totale mtot = mv1 + ml1 :
x1 =
mv1
= 0.09
mtot
(8.1)
Poichè il volume del contenitore non cambia, e non vi sono scambi di massa
con l'ambiente, si avrà che il v1 = v2 . In entrambi gli stati il volume specico
della miscela si può calcolare come media pesata dei volumi specici del
liquido saturo e del vapore saturo
v1 = x1 vv1 + (1 − x1 )vl1 = x2 vv2 + (1 − x2 )vl1 = v2
10
(8.2)
Figura 8.2:
Estratto delle tabelle del vapore saturo.
Dalle tabelle del vapore saturo, di cui è riportato un estratto in Fig. 8.2,
si ricavano i valori dei volumi specici in corrispondenza delle curve limite:
vl1 = 0.001043 m3 /kg
vl2 = 0.001093 m3 /kg
vv1 = 1.6940 m3 /kg
vv2 = 0.3748 m3 /kg
(8.3)
Sostituendo i valori nell'eq. 8.2 e risolvendo per x2 si ottiene:
x2 =
x1 vl1 + (1 − x1 )vv1 − vl2
= 0.408
vv2 − vl2
(8.4)
Il calore somministrato al sistema si calcola attraverso il primo principio
per sistemi chiusi, nell'ipotesi di lavoro nullo
∆U = Q + L = Q
(8.5)
La variazione di energia interna può essere calcolata come ∆U = mtot (u2 −
u1 ), dove l'energia interna specica iniziale e nale è calcolata per interpolazione dalle tabelle del vapore.
u1 = x1 uv1 + (1 − x1 )ul1
u2 = x2 uv2 + (1 − x2 )ul2
11
(8.6)
Se nelle tabelle del vapore a disposizione i valori dell'energia interna non
fossero direttamente tabellati, come nel caso di Fig. 8.2, possono essere
ricavati dal valore dell'entalpia attraverso la denizione di entalpia stessa
h = u + pv :
uv1 = hv1 − p1 vv1 = 2675 × 103 J/kg − 1 × 105 Pa1.694 m3 /kg
= 2506 × 103 J/kg
ul1 = hl1 − p1 vl1 = 417 × 103 J/kg
uv2 = hv2 − p2 vv2 = 2561 × 103 J/kg
ul2 = hl2 − p2 vl2 = 812 × 103 J/kg
(8.7)
Si presti particolare attenzione all'utilizzo delle unità di misura nelle eq. 8.7,
J per l'energia e Pa (anzichè bar) per la pressione, al ne di ottenere la'omogeneit`a dimensionale dell'equazione. Utilizzando inne i valori in eq. 8.7,
l'eq. 8.6 ed il primo principio per sistemi chiusi si ottiene il calore scambiato
Q = ∆U = mtot (u2 − u1 ) = 2278 kJ
12
(8.8)