Compito di matematica Classe 3A 22 Febbraio 2010 Alunno

Compito di matematica Classe 3A 22 Febbraio 2010 Alunno
Problema 1
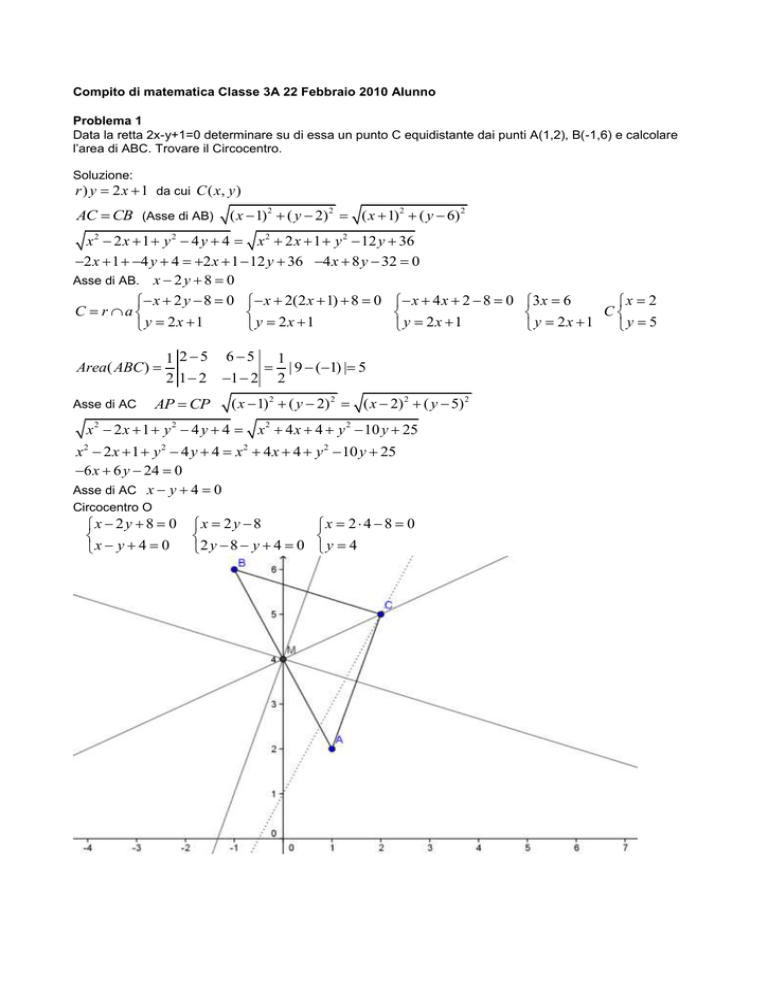
Data la retta 2x-y+1=0 determinare su di essa un punto C equidistante dai punti A(1,2), B(-1,6) e calcolare
l’area di ABC. Trovare il Circocentro.
Soluzione:
r ) y  2 x  1 da cui C ( x, y )
AC  CB (Asse di AB)
( x  1) 2  ( y  2) 2  ( x  1) 2  ( y  6) 2
x 2  2 x  1  y 2  4 y  4  x 2  2 x  1  y 2  12 y  36
2 x  1  4 y  4  2 x  1  12 y  36 4 x  8 y  32  0
Asse di AB. x  2 y  8  0
 x  2 y  8  0  x  2(2 x  1)  8  0  x  4 x  2  8  0 3 x  6
x  2
C  r a
C



 y  2x  1
 y  2x 1
 y  2x 1
 y  2x 1
y  5
Area( ABC ) 
Asse di AC
1 25 65 1
 | 9  (1) | 5
2 1  2 1  2 2
AP  CP
( x  1) 2  ( y  2) 2  ( x  2) 2  ( y  5) 2
x 2  2 x  1  y 2  4 y  4  x 2  4 x  4  y 2  10 y  25
x 2  2 x  1  y 2  4 y  4  x 2  4 x  4  y 2  10 y  25
6 x  6 y  24  0
Asse di AC x  y  4  0
Circocentro O
x  2 y  8  0

x  y  4  0
x  2 y  8
x  2  4  8  0


2 y  8  y  4  0  y  4
Problema 2
Dati due punti A(2,2) B(5,3), determinare sulla retta di equazione 3x-y=6 un punto C tale che l’area del
triangolo ABC misuri 5. Inoltre trovare sul segmento AB un punto D tale che AD=2BD
r )3 x  y  6 da cui C ( x, y ) C ( x,3 x  6)
Area( ABC ) 
1 yC  y A
2 xC  xA
1
| 8 x  22 | 5 
2
yB  y A 1 3 x  6  2 3  2 1 3 x  8 1 1


 | 9 x  24  x  2 | 5
xB  xA 2 x  2
52 2 x 2 3 2
| 8 x  22 | 10
1)
8x  22  10  x  4  C (4, 6)
2)
8x  22  10  x 
3
3 3
 C( ,  )
2
2 2
D ( x, y )  xD  xA  2( xB  xD )  x  2  2(5  x)  x  4
yD  y A  2( yB  yD ) 
Oppure:
la retta AB ha equazione: m 
y  2  2(3  y) 
3y  8 
y
8
 8
 D   4, 
3
 3
3 2 1
1
1
4
  y  2  ( x  2)  y  x 
52 3
3
3
3
AD  2 DB  xD  xA 1  m2  2 ( xB  xD ) 1  m2 
1) x  2  2(x  5) 
2) x  2  2(x  5) 
x4  y 
4 4 8
 8
 
 D   4, 
3 3 3
 3
8 4 12
x  8  y     4 (non accettabile, perché esterno ad AB)
3 3 3
Problema 3
Di un triangolo rettangolo isoscele si sa che il vertice dell’angolo retto è A(2,1) e l’equazione della retta BC è
y=8-2x. Determinare i vertici B e C.
Soluzione.
Per prima cosa trovo l’altezza relativa all’ipotenusa (retta per A e perpendicolare a BC). E il piede
dell’altezza H.
Dato che il coefficiente angolare di BC è m=-2
1
1
( x  2)
y x
2
2
8
1


1
1
1
y
y x







y  x
y  x
y  x
5
2
Da cui H 
H
H
H
H
2
2
2
 1 x  2 x  8
 x  16


5 x  16
x  4 x  16
 y  2 x  8

 2

5
Altezza AH: y  1 
Ora calcolo la lunghezza dell’altezza AH. (distanza punto retta o distanza AH)
AH 
| 2 xA  y A  8 | 3

4 1
5
In un triangolo rettangolo isoscele BH=CH=AH. e B e C appartengono alla retta y=-2x+8
B, C  x; 2 x  8
Quindi
| x
BH | xB  xH | 1  m 2
16
3
| 5
5
5
1) x 
19
 19 2 
C ; 
5
 5 5
|
BH | x 
5 x  16
3
| 5
5
5
5
2) x 
13
5
16
3
| 1 4 
5
5
| 5 x  16 | 3
 13 14 
B ; 
5 5
Compito di matematica Classe 3B
04/03/2017 Alunno
Problema 1
Data la retta 2x-y+1=0 determinare su di essa un punto C equidistante dai punti A(1,2), B(-1,6) e calcolare
l’area di ABC. Trovare il Circocentro.
Problema 2
Dati due punti A(2,2) B(5,3), determinare sulla retta di equazione 3x-y=6 un punto C tale che l’area del
triangolo ABC misuri 5. Inoltre trovare sul segmento AB un punto D tale che AD=2BD
Problema 3
Di un triangolo rettangolo isoscele si sa che il vertice dell’angolo retto è A(2,1) e l’equazione della retta BC è
y=8-2x. Determinare i vertici B e C.