PROGETTO LAUREE SCIENTIFICHE
Lic e o Norbert o Rosa
MATEMATICA
MODULO DI ALGEBRA MODERNA
SIMULAZIONE
TEST FINALE
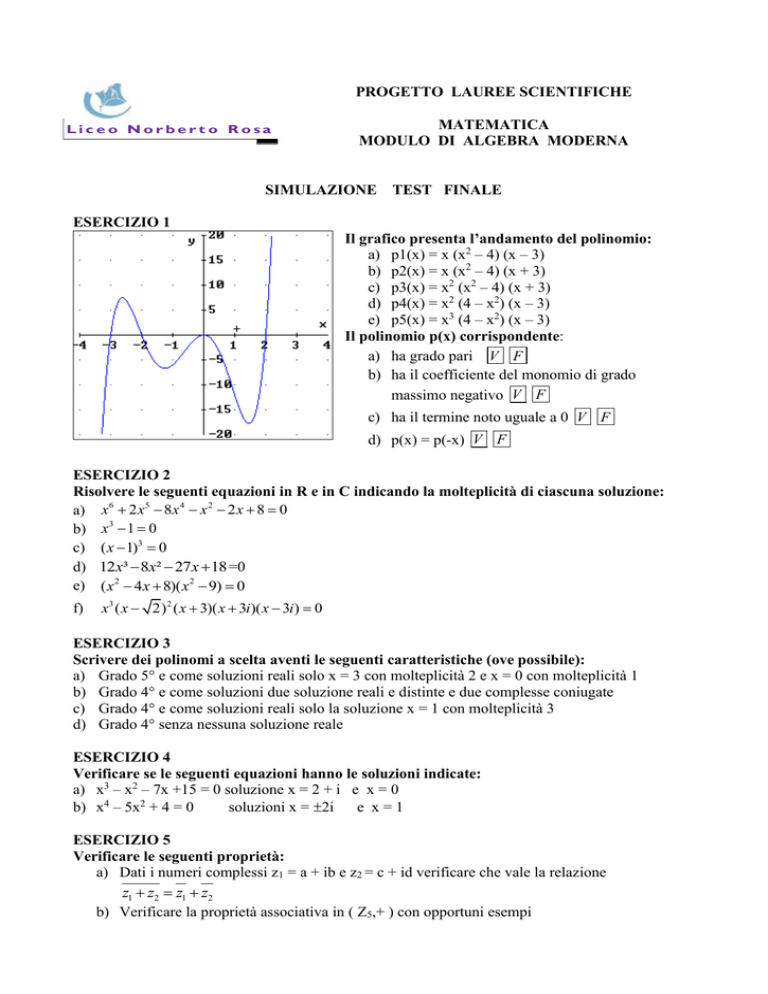
ESERCIZIO 1
Il grafico presenta l’andamento del polinomio:
a) p1(x) = x (x2 – 4) (x – 3)
b) p2(x) = x (x2 – 4) (x + 3)
c) p3(x) = x2 (x2 – 4) (x + 3)
d) p4(x) = x2 (4 – x2) (x – 3)
e) p5(x) = x3 (4 – x2) (x – 3)
Il polinomio p(x) corrispondente:
a) ha grado pari V F
b) ha il coefficiente del monomio di grado
massimo negativo V F
c) ha il termine noto uguale a 0 V F
d) p(x) = p(-x) V F
ESERCIZIO 2
Risolvere le seguenti equazioni in R e in C indicando la molteplicità di ciascuna soluzione:
a) x 6 2 x5 8 x 4 x 2 2 x 8 0
b) x 3 1 0
c) ( x 1)3 0
d) 12x³ 8x² 27x 18 =0
e) ( x2 4 x 8)( x 2 9) 0
f)
x3 ( x 2)2 ( x 3)( x 3i )( x 3i ) 0
ESERCIZIO 3
Scrivere dei polinomi a scelta aventi le seguenti caratteristiche (ove possibile):
a) Grado 5° e come soluzioni reali solo x = 3 con molteplicità 2 e x = 0 con molteplicità 1
b) Grado 4° e come soluzioni due soluzione reali e distinte e due complesse coniugate
c) Grado 4° e come soluzioni reali solo la soluzione x = 1 con molteplicità 3
d) Grado 4° senza nessuna soluzione reale
ESERCIZIO 4
Verificare se le seguenti equazioni hanno le soluzioni indicate:
a) x3 – x2 – 7x +15 = 0 soluzione x = 2 + i e x = 0
b) x4 – 5x2 + 4 = 0
soluzioni x = 2i
e x=1
ESERCIZIO 5
Verificare le seguenti proprietà:
a) Dati i numeri complessi z1 = a + ib e z2 = c + id verificare che vale la relazione
z1 z2 z1 z2
b) Verificare la proprietà associativa in ( Z5,+ ) con opportuni esempi
c) Date le tre seguenti matrici quadrate verificare che la vale la proprietà distributiva del
prodotto rispetto alla somma
2 1
0 3
1 0
A
B
C
0 1
1 2
0 2
ESERCIZIO 6
Enunciare:
a) Teorema fondamentale dell’algebra
b) Definizione di gruppo e di sottogruppo
c) Definizione di campo
d) Definizione di classe di resto modulo 7
e) Enunciare il teorema di Ruffini
ESERCIZIO 7
Fare un esempio di:
a) Anello
b) Di due matrici A e B per cui è possibile calcolare AB e non BA
c) Di un insieme Zn che non verifiche la legge di annullamento del prodotto
ESERCIZIO 8
Disegnare nel piano di Gauss i numeri complessi:
-2 ; 3i ; 1 - i ; -1 + 2i:
z1 = 2 + 3i ; z2 = - 1 + 2i ; z1 + z2 ; z1 - z2:, i z1
z3 2;
4
2
z4 1;
3
z3 z4
z3 / z4
Scrivere almeno 2 dei precedenti numeri complessi sia in forma algebrica che in forma
trigonometrica
ESERCIZIO 9
Disegnare nel piano di Gauss e determinare tutti i numeri complessi la cui terza potenza è 8.
ESERCIZIO 10
Trovare il più piccolo intero positivo m tale che [m] = [325] in Z7 e il più piccolo intero positivo
x tale che [26] + [x] = [0] in Z17.
ESERCIZIO 11
Calcolare le potenze [5]n con n=2,3,4,5 in Z6
RISOLUZIONE
ESERCIZIO 1
Il grafico presenta l’andamento del polinomio: p3(x) = x2 (x2 – 4) (x + 3)
Il polinomio p(x) corrispondente: ha il termine noto uguale a 0
ESERCIZIO 2
Risolvere le seguenti equazioni in R e in C indicando la molteplicità di ciascuna soluzione:
a) x 6 2 x5 8 x 4 x 2 2 x 8 0
In R: x = -4, x = 1, x = 2 … in C inoltre x = i
3
b) x 1 0
1 3i
In R: x = 1 … in C inoltre x
2
3
c) ( x 1) 0
In R e in C: x = 1 con molteplicità 3
d) 12x³ 8x² 27x 18 =0
In R e in C: x = 2/3, x = 3/2
2
e) ( x 4 x 8)( x 2 9) 0
In R x = 3 … in C inoltre : x = 2 2i
3
f) x ( x 2)2 ( x 3)( x 3i )( x 3i ) 0
In R x = 0 (molt. =3), x = 2 (molt. 2), x = -3… in C inoltre: x = 3i
ESERCIZIO 3
Scrivere dei polinomi a scelta aventi le seguenti caratteristiche (ove possibile):
a) Grado 5° e come soluzioni reali solo x = 3 con molteplicità 2 e x = 0 con molteplicità 1
x5 6 x 4 10 x3 6 x 2 9 x x( x 3)2 ( x 2 1) 0
b) Grado 4° e come soluzioni due soluzione reali e distinte e due complesse coniugate
x 4 16 ( x 2 4)( x 2 4) 0
c) Grado 4° e come soluzioni reali solo la soluzione x = 1 con molteplicità 3
Non possibile perché le soluzioni complesse sono sempre accoppiate
d) Grado 4° senza nessuna soluzione reale
x 4 5x 2 4 ( x 2 1)( x 2 4) 0
ESERCIZIO 4
Verificare se le seguenti equazioni hanno le soluzioni indicate:
a) x3 – x2 – 7x +15 = 0 soluzione x = 2 + i e x = 0
x = 2 + i SI - x = 0 NO
4
2
b) x – 5x + 4 = 0
soluzioni x = 2i
e x=1
x = 2i NO - e x = 1 SI
ESERCIZIO 5
Verificare le seguenti proprietà:
a) Dati i numeri complessi z1 = a + ib e z2 = c + id verificare che vale la relazione z1 z2 z1 z2
z1 z2 (a ib) (c id ) (a c) i (b d )
(a c) i (b d ) (a ib) (c id ) z1 z2
b) Verificare la proprietà associativa in ( Z5,+ ) con opportuni esempi
3 2 4 3 2 4
0 4 3 1
4 4
c) Date le tre seguenti matrici quadrate verificare che la vale la proprietà distributiva del prodotto
rispetto alla somma
2 1
0 3
1 0
A
B
C
0 1
1 2
0 2
2 1 0
A *( B C )
*
0 1 1
2 1 0
A* B A*C
*
0 1 1
3 1 0 2 1 2 0 4 4
*
2 0 2 0 1 0 4 0 4
3 2 1 1 0 2 2 2 2 4 4
2 0 1 0 2 0 2 0 2 0 4
ESERCIZIO 6
Enunciare vedere le presentazioni dei 7 moduli
a) Teorema fondamentale dell’algebra
b) Definizione di gruppo e di sottogruppo
c) Definizione di campo
d) Definizione di classe di resto modulo 7
e) Enunciare il teorema di Ruffini
ESERCIZIO 7
Fare un esempio di:
a) Anello
Anello delle classi di resto modulo n, Anello delle matrici
b) Di due matrici A e B per cui è possibile calcolare AB e non BA
1 0
2 1 0 7
A(3, 2) 3 2
B(2, 4)
1 0 3 5
4 9
c) Di un insieme Zn che non verifiche la legge di annullamento del prodotto:
Z6 , infatti 2 3 0
ESERCIZIO 8
Disegnare nel piano di Gauss i numeri complessi:
-2 ; 3i ; 1 - i ; -1 + 2i:
z1 = 2 + 3i ; z2 = - 1 + 2i ; z1 + z2 ; z1 - z2:, i z1
z3 2;
4
2
z4 1;
3
2
11
z3 z4 1 2;
2;
4 3
12
2
2
5
z3 / z4 ;
2;
1
4 3
12
Scrivere almeno 2 dei precedenti numeri complessi sia in forma algebrica che in forma
trigonometrica
z3 2; 2 i 2
4
z 3; 3i
2
ESERCIZIO 9
Disegnare nel piano di Gauss e determinare tutti i numeri complessi la cui terza potenza è 8.
2) w 3 8
w0 2 cos 0 isen0
z 1
n 3
2
0
2
2
w1 2 cos isen
3
3
4
4
w2 2 cos isen
3
3
ESERCIZIO 10
Trovare il più piccolo intero positivo m tale che [m] = [325] in Z7 e il più piccolo intero positivo
x tale che [26] + [x] = [0] in Z17.
Soluzione: [x]= [8]
ESERCIZIO 11
Calcolare le potenze [5]n con n=2,3,4,5 in Z6
52 25 1; 53 5; 54 1; 55 5












