Tutorato di Fisica 2 – 02/12/2016
Problema 1 (Appello 20/07/2015)
Un elettromagnete e costituito da un materiale ferromagnetico
H (A/m)
B (T)
per cui la relazione esistente tra B e H e mostrata per alcuni va1000
0.2
lori di H nella tabella. La lunghezza della parte ferromagnetica
1500
0.7
dell’elettromagnete e L = 80 cm mentre la sezione e Σ = 40 cm2.
2000
1.1
L’elettromagnete presenta un traferro in aria di lunghezza
d = 1 cm. Supponendo che la bobina di alimentazione sia costi2500
1.4
tuita da N = 50 spire, determinare la corrente necessaria a
3000
1.6
creare nel traferro un campo di induzione magnetica B1 = 1 T
oppure B2 = 0.5 T. Si supponga di approssimare la curva di isteresi con una curva lineare a tratti
passante per i punti indicati in tabella.
Problema 2 (Appello 31/08/2015)
Su una spira quadrata di lato h = 5 m e posto un condensatore piano con distanza fra le armature
d = 0.2 mm. Il condensatore e riempito con un dielettrico che presenta una rigidita dielettrica
ER = 1 kV/mm. Determinare la velocita costante v massima con cui la spira puo penetrare nel campo magnetico B = 2 T affinche all’interno del condensatore non
si verifichi una scarica.
Problema 3
Si consideri un avvolgimento composto da 500 spire di rame (ρ = 1.7 x 10–8 Ωm e sezione del
filo s = 5 mm2) di sezione circolare di raggio r = 1 cm e lunghezza d = 1 m. All’istante t = 0 le
spire vengono alimentate con una tensione a gradino pari a 60 V. Quanto vale l’energia magnetica accumulata nella bobina al tempo t = 20 ms. Si supponga ora che l’avvolgimento venga interamente riempito con un materiale ferromagnetico caratterizzato da una permeabilita
μr = 200. Quanto vale in questo caso l’energia magnetica accumulata nella bobina al tempo
t = 20 ms
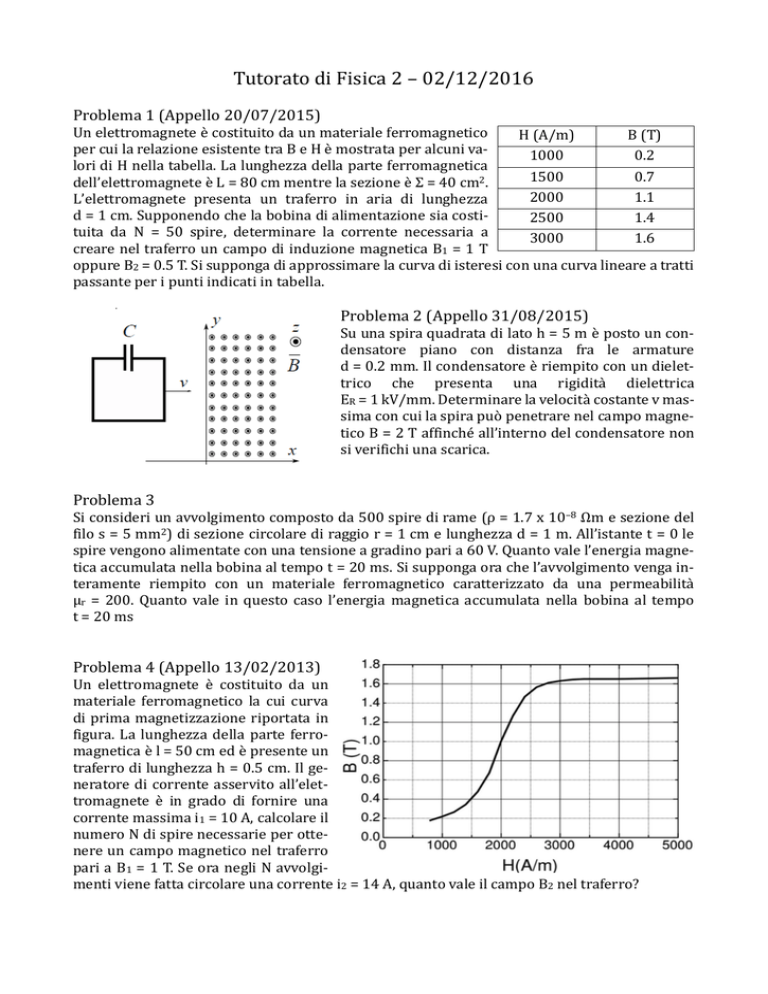
Problema 4 (Appello 13/02/2013)
Un elettromagnete e costituito da un
materiale ferromagnetico la cui curva
di prima magnetizzazione riportata in
figura. La lunghezza della parte ferromagnetica e l = 50 cm ed e presente un
traferro di lunghezza h = 0.5 cm. Il generatore di corrente asservito all’elettromagnete e in grado di fornire una
corrente massima i1 = 10 A, calcolare il
numero N di spire necessarie per ottenere un campo magnetico nel traferro
pari a B1 = 1 T. Se ora negli N avvolgimenti viene fatta circolare una corrente i2 = 14 A, quanto vale il campo B2 nel traferro?
Problema 5
Il circuito in figura e costituito da tre resistenze R1= 10 Ω, R2= 20 Ω, R3= 30 Ω, una induttanza
L= 2 H, un generatore con f.e.m. V = 100 V e un interruttore S inizialmente aperto. Calcolare le
correnti i1, i2 sulle resistenze R1, R2 nelle seguenti condizioni:
immediatamente dopo la chiusura di S;
a regime con S chiuso;
immediatamente dopo l’apertura di S immediatamente dopo l’apertura di (una volta
raggiunto la condizione di regime);
a regime con S aperto.
Problema 6 (Appello 26/08/2016)
Un circuito elastico conduttore di forma circolare, con resistenza per unita di lunghezza ρ = 2
Ω/m, e immerso in un campo B uniforme di modulo 2 T, inclinato di 45° rispetto al piano del
circuito. Il raggio dell’elastico varia con legge r(t ) = rm[1+α sin(2t )] (tempo in sec), rm = 10 cm
e α = 0.1. Calcolare la corrente di picco indotta e la potenza media dissipata. (approssimare
notando che la variazione % del raggio e piccola!)
Problema 7 (Appello 01/09/2014)
Si consideri il circuito rappresentato in figura.
Il resistore R2 = 25 Ω mentre il resistore R1 e
costituito da un filo di tungsteno
(ρ = 5.26 · 10−8 Ωm) di lunghezza h = 38 m e
sezione S = 0.4 mm2; il condensatore C1 ha
facce piane e parallele di area A = 4 cm2,
distanti d = 2 mm ed e completamente
riempito di un dielettrico di costante ke = 4.5,
mentre l’induttore L1 e costituito da un
solenoide di sezione Σ = 3 mm2 e lunghezza
l = 6 cm con n = 90 spire/cm ed e completamente riempito di un nucleo ferromagnetico
(km = 100). A regime si calcoli:
la caduta di tensione ai capi di R2;
la potenza dissipata nel resistore R1;
l’energia immagazzinata nel condensatore e nell’induttore.
Problema 8
Si consideri una spira di corrente in cui circola una corrente I = 2 mA. La spira ha sezione S = 4
cm2. Quanto vale il flusso del campo magnetico attraverso una superficie chiusa che contiene la
spira?












