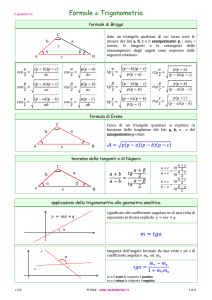
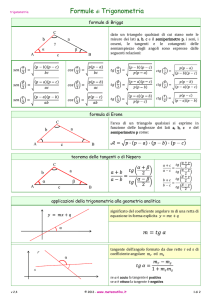
UNITA’ 5. LA TRIGONOMETRIA E I TEOREMI SUI TRIANGOLI.
1. Introduzione alla trigonometria.
2. Le origini della trigonometria.
3. I teoremi sui triangoli rettangoli.
4. La risoluzione di un triangolo rettangolo.
5. L’area di un triangolo.
6. Il teorema della corda.
7. Il teorema dei seni.
8. Il teorema del coseno.
9. La risoluzione di un triangolo generico.
10. La formula di Erone.
11. Raggio della circonferenza inscritta e circoscritta ad un triangolo.
12. Esercizi vari e problemi di applicazione.
1. Introduzione alla trigonometria.
La trigonometria (dal greco trigonon = triangolo e metron = misura) è la parte della
matematica che studia tutte le possibili relazioni che ci possono essere tra gli angoli e i lati di
un triangolo in modo che, conoscendo alcuni di questi elementi, sia possibile calcolare gli
altri.
Di un triangolo, infatti, quando sono noti tre dei suoi elementi, di cui almeno un lato, è
possibile calcolare tutti gli altri elementi utilizzando opportune formule di trigonometria.
E’ anche possibile utilizzare le formule di trigonometria per risolvere problemi più complessi
che riguardano poligoni con più lati o figure geometriche solide, scomponendoli
opportunamente in più triangoli.
La trigonometria ha anche numerose applicazioni in Fisica ( per esempio nel calcolo
vettoriale), in Topografia (per esempio nel misurare l’altezza di un montagna) e in
Astronomia (per esempio nel determinare la posizione dei pianeti).
2. Le origini della trigonometria.
Lo studio sistematico della trigonometria è iniziato ad opera di antichi scienziati, che erano
più astronomi che matematici.
La trigonometria, infatti, nacque con l’obiettivo di perfezionare lo studio dell’astronomia, in
modo da prevedere il moto dei corpi celesti, determinare l’ora con precisione e compilare i
calendari.
Il greco Ipparco di Nicea, intorno all’anno 150 a. C., seguendo il sistema babilonese di
dividere la circonferenza in 360 parti, e ciascuna di queste in 60 primi e 60 secondi, fu il
primo a compilare delle tavole trigonometriche che gli permettevano di risolvere qualsiasi
triangolo. Grazie ai suoi calcoli e alle sue numerose osservazioni astronomiche, è stato il
primo a sviluppare un metodo per la previsione delle eclissi solari, scoprì la precessione degli
equinozi e compilò un celebre catalogo stellare.
Menelao di Alessandria, intorno all’anno 100 d. C., è stato un grande matematico e
astronomo che ha contribuito allo studio e alle applicazioni della trigonometria. Scrisse un
trattato in tre libri dal titolo “Sphaerica” in cui sviluppò la geometria sferica, la applicò nel
campo dell’ Astronomia e introdusse la trigonometria sferica.
L’egiziano Claudio Tolomeo, intorno all’anno 150 d. C., contribuì a sviluppare ulteriormente
la trigonometria piana, ma si dedicò soprattutto alla trigonometria sferica, poiché questa si
poteva applicare meglio allo studio dell’astronomia. Nella sua opera principale, l’Almagesto,
egli diede alla trigonometria quell’aspetto preciso e rigoroso che avrebbe poi mantenuto per
oltre 1000 anni. Egli aveva già dimostrato le formule di addizione del seno e del coseno e la
formula di bisezione del seno, compilando una tabella di valori per numerosi angoli.
Con i suoi studi e con quelli precedenti di Ipparco formulò il famoso sistema geocentrico con
la Terra al centro dell’universo. Tale modello, che da lui prese il nome di sistema tolemaico,
rimase come riferimento in tutto il mondo occidentale finché, molti anni dopo, non fu
sostituito dal sistema eliocentrico dall’astronomo polacco Niccolò Copernico.