I NUMERI AMICI (O AMICABILI )
°°°°°°°°°°
Gruppo ERATOSTENE, Prof. Carmelo Di Stefano
Riassunto
In questo lavoro riporteremo alcuni brani sui numeri amici (detti
anche amicabili, o anche persiani), che, sebbene non primi, hanno
delle connessioni con i numeri primi, sebbene praticamente e
apparentemente poco utili allo studio della teoria dei numeri (ma,
in matematica…non si può mai sapere). Accenneremo comunque
alla loro distribuzione, e ad una possibile e attendibile (almeno
inizialmente) stima logaritmica del loro numero fino a 10^n e alle
loro forme 6k-2 oppure 6k +2 di ognuno di loro, per ogni coppia;
e mai dello stesso segno; i numeri perfetti, tranne il 6 iniziale,
sono invece tutti di forme 6k-2 (con dimostrazione finale).
Cominciamo con Wikipedia voce “Numeri amicabili”, con
accenni ai numeri “fidanzati”, “socievoli”, ecc.
“In matematica, sono numeri amicabili o amici due numeri per cui la somma dei divisori di uno
(escluso il numero stesso) è uguale all'altro e viceversa.
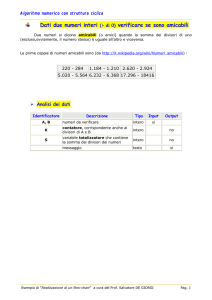
Un esempio classico è dato dalla coppia 220 e 284. I due numeri sono amicabili in quanto
•
•
220 è divisibile per 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110 e la loro somma risulta 284;
284 è divisibile per 1, 2, 4, 71, 142 che sommati tra loro restituiscono proprio 220.
Altri numeri amicabili sono ad esempio le coppie 1184 e 1210, 2620 e 2924, 5020 e 5564, 17296 e
18416.
Negli ultimi dieci anni la ricerca di numeri amicabili ne ha fatto lievitare esponenzialmente la
quantità. Al giugno 2006 ne erano noti poco più di 11 milioni, di cui alcuni con migliaia di cifre.
Se un numero è amicabile di se stesso, cioè se la somma dei suoi divisori (escluso il numero stesso)
è uguale a se stesso (come il numero 28), è chiamato numero perfetto.
Nella storia [modifica]
In epoca greca, i numeri amicabili erano noti ai pitagorici, che attribuivano loro un valore mistico.
Nel IX secolo, il matematico arabo Thābit b. Qurra al-Ḥarrānī al-Ṣābi
per definire alcune coppie amicabili:
(826-901) trovò un metodo
fissato n intero positivo, se i numeri:
p = 3 2n-1 - 1
q = 3 2n - 1
r = 9 22n-1 - 1
sono tre primi dispari, allora la coppia (2npq,2nr) è una coppia di numeri amicabili
Non tutte le coppie di numeri amici si ottengono con queste formule: un esempio è (1184, 1210).
Nella matematica occidentale moderna, vari celebri studiosi hanno ricercato coppie di amici:
•
•
•
Fermat nel 1636 annunciò di avere trovato la coppia (17296,18416), che però era
sicuramente già nota all'arabo Ibn al-Banna de Marrakech (1256-1321), e probabilmente
anche al citato Thābit ibn Qurra, poiché si ottiene dalla sua formula per n = 4.
Cartesio trovò (9363584, 9437056), che si ottiene dalla solita formula per n=7.
Eulero pubblicò nel 1750 una lista comprendente 60 coppie di numeri amicali, ignorando
curiosamente la seconda in ordine di grandezza (1184, 1210), che venne poi scoperta nel
1866 da Niccolò Paganini, un giovane studente di 16 anni omonimo del famoso violinista.
Proprietà [modifica]
In tutti i casi conosciuti, i numeri di una coppia sono o entrambi pari o entrambi dispari, nonostante
non siano note ragioni per cui questo debba avvenire necessariamente. Inoltre, ogni coppia
conosciuta condivide almeno un fattore.
Non si sa se esistano coppie di numeri coprimi amicabili, ma se esistono è dimostrato che il loro
prodotto deve essere maggiore di 1067.
Numeri Socievoli [modifica]
Un gruppo di numeri socievoli è un insieme di numeri in cui ogni numero è amicabile del numero
posto accanto ad esso, ed il primo è amicabile dell'ultimo, cosicché i numeri formino una sorta di
"catena ciclica". Nel 1918, il matematico Paul Poulet scoprì il gruppo di numeri socievoli 12 496,
14 288, 15 472, 14 536, 14 264 Se sommiamo i divisori propri di 14 264, otteniamo 1 + 2 + 4 + 8 +
1 783 + 3 566 + 7 132 = 12 496, ovvero il numero che nell'ordine del gruppo viene subito dopo di
lui, quindi 12 264 è amicabile di 12 496; il ciclo si ripete nello stesso modo per tutti i numeri. La
più lunga catena di numeri socievoli conosciuta è stata scoperta da Ren Yuanhua, e conta 54 numeri.
Numeri Fidanzati [modifica]
I numeri fidanzati sono numeri tali che la somma dei divisori di uno (escluso il numero stesso e, a
differenza dei numeri amicabili, anche l'1) dà come risultato un altro, e viceversa. Le coppie di
numeri amicabili e le catene di numeri socievoli sono sempre o tutti pari o tutti dispari. Si può
osservare, invece, che due numeri fidanzati sono sempre uno pari e l'altro dispari; infatti, Pitagora
distinse i numeri pari come femminili e i numeri dispari come maschili. La prima coppia di numeri
fidanzati, detti anche promessi sposi, è 48 e 75; la coppia più grande nota oggi invece è 2102750 e
2681019 “
Qui riportiamo il contributo del Prof. Carmelo di Stefano:
“
Due numeri naturali m ed n si dicono amici se la somma delle parti proprie di uno è
uguale all’altro numero e viceversa.
Per esempio 220 e 284 sono amici dato che la somma dei divisori propri di 220 è
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
E allo stesso modo la somma dei divisori propri di 284 è
1 + 2 + 4 + 71 + 142 = 220.
La giustificazione della terminologia è la seguente: dato che ciascun numero è somma delle parti
proprie dell’altro vuol dire che i due sono parte uno dell’altro, sono quindi come amici fraterni.
Sembra che i primi ad indagare tali numeri siano stati i Pitagorici. Comunque anche nella
matematica araba essi hanno giocato un ruolo molto importante, come ci ricorda Oystein Ore che
riporta una citazione di un passo di Ibn Khaldun, vissuto dal 1331 al 1406: «Persone che si
occupano di magia assicurano che questi numeri hanno una particolare influenza nello stabilire
unione ed amicizia fra due individui. [...] Essi stabiliscano un legame così forte fra due persone che
esse non possono essere più separate. L’autore di Ghaïa e di altri capolavori in quest’arte [la
magia] dichiarano che ciò è stato confermato dalla loro esperienza personale.1».
È interessante notare che nonostante questo interesse della numerologia, per molti secoli l’unica
coppia di numeri amici conosciuta fu (220, 284). Si dovette arrivare al solito Fermat per ottenere
altre coppie di numeri amici. Il fatto è alquanto strano, poiché il matematico francese determinò una
formula utilizzando dei risultati che l’arabo Abu–l–Hasan Thabit ben Korrah2 aveva stabilito nel IX
secolo.
Il risultato di Fermat è il seguente.
Teorema. Siano pn = 3⋅2n –1 e qn = 9⋅22n–1 – 1. Se esiste un numero naturale n per cui pn–1, pn e qn
sono tutti numeri primi, allora i numeri 2n ⋅pn–1⋅ pn e 2n ⋅qn sono amici.
Con questa formula Fermat nel 1636 determinò un’altra coppia di numeri amici. Infatti, visto che p3
= 3⋅23 – 1 = 23, p4 = 3⋅24 – 1 = 47 e q4 = 9⋅27 – 1 = 1151, sono tutti primi, possiamo dire che i
numeri 24⋅23⋅47 = 17296 e 24⋅1151 = 18416 sono amici. In una lettera a Mersenne 3 del 1638
Cartesio annunciò di essere arrivato autonomamente allo stesso risultato e fornì la terza coppia di
numeri amici: 9 363 584 e 9 437 056. Nel 1747 Eulero diede una lista di 30 coppie di numeri amici,
che successivamente aumentò a 60.
La formula di Fermat genera poche coppie di numeri amici. Per esempio, usando Derive troviamo
solo 3 coppie inferiori a 10 milioni.
1
O. Ore, The theory of numbers and its history
Come per molti arabi la scrittura occidentale del suo nome è spesso contrastata, per esempio qualcuno scrive anche
Al-Sabi Thabit ibn Qurra al-Harrani. Questi nacque nel 836 nell’odierna Turchia e morì a Bagdad nel 901. Fu un
membro della setta dei Sabiani che adoravano le stelle. Perciò si interessò di astronomia, ma anche di medicina e
matematica. In particolare effettuò un’importante traduzione degli Elementi euclidei, che solo grazie alle traduzioni
arabe è potuto arrivare sino a noi, come del resto molti altri antichi testi greci, di tutte le discipline. Come
matematico si interessò soprattutto di risultati di teoria dei numeri.
3
Nato nel 1588 e morto nel 1648, Marin Mersenne, studiò nella prestigiosa scuola dei Gesuiti di La Flèche. Nel 1611
prese i voti nell’Ordine dei Frati Minimi, soprattutto perché la vita monastica gli consentiva di potere proseguire
facilmente nei propri studi. Cominciò così a interessarsi di Matematica e cominciò a corrispondere con i più famosi
scienziati e uomini di cultura del tempo, da Gassendi a Descartes, da Roberval a Fermat, da Hobbes a Pascal. Il suo
nome è oggi legato ai numeri primi della forma 2p – 1, noti appunto come numeri di Mersenne, e che molta
importanza hanno nella ricerca dei numeri perfetti.
2
Li troviamo però in tempi rapidi, in 25,6 secondi con un processore Intel da 2,80 Ghz e 1 Gb di
Ram. Questo tempo serve a verificare per i primi 1000 valori di n quali terne sono prime, i valori
effettivi poi li troviamo in tempi prossimi allo zero, poiché sono semplici calcoli numerici.
Invece, sempre con Derive possiamo costruire un generatore di numeri amici meno efficiente per i
tempi, ma efficace nel senso che, almeno in linea teorica, trova tutte le coppie.
Abbiamo definito una funzione, sfruttando il comando predefinito DIVISORS, che calcola la
somma dei divisori di un numero escluso il numero stesso. Quindi selezioniamo tutti quei numeri
per i quali la somma dei divisori della somma dei divisori coincidono con il numero stesso. Per i
primi 1000 numeri troviamo i risultati in appena 1,64 secondi. In questo modo però troviamo anche
i numeri perfetti, che ovviamente sono autoamici, quindi modifichiamo la selezione cercando
soltanto le coppie diverse di numeri amici.
Troviamo ancora 1, ma basta partire da 2 e il problema si risolve. Osserviamo che il calcolo avviene
in 2,50 secondi. Quindi il controllo che il numero non fosse autoamico ha aumentato i tempi di
calcolo di più del 50%. Applichiamo la formula ai primi 20000 numeri.
Troviamo ben 8 coppie, contro le 2 della formula di Fermat, ma lo facciamo in un tempo di ben
72,5 secondi. Provando senza il controllo sui numeri perfetti, riduciamo i tempi di calcolo a 49
secondi, con un risparmio del 32%.
Per inciso i numeri perfetti trovati sono 6, 28, 496 e 8128. Andare a calcolare con questo algoritmo
la terza coppia trovata da Fermat sicuramente produrrebbe tempi di calcolo molto grandi”
Da Wolfram Mathworld , voce ”Amicable Pair”, riportiamo:
Amicable Pair
An amicable pair
consists of two integers
for which the sum of proper divisors (the divisors excluding the number itself) of one
the other. Amicable pairs are occasionally called friendly pairs (Hoffman 1998, p. 45), although this nomenclature is to be discouraged s
more commonly known as friendly pairs are defined by a different, albeit related, criterion. Symbolically, amicable pairs satisfy
Where
is the restricted divisor function. Equivalently, an amicable pair
where
satisfies
is the divisor function. The smallest amicable pair is (220, 284) which has factorizations
giving restricted divisor functions
The quantity
in this case,
, is called the pair sum. The first few amicable pairs are (220, 284), (1184, 1210), (2620, 2924) (5020, 556
(10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084), ... (Sloane's A002025 and A002046). An exhaustive tabulation is mai
D. Moews.
In 1636, Fermat found the pair (17296, 18416) and in 1638, Descartes found (9363584, 9437056), although these results were actually
numbers known to Arab mathematicians. By 1747, Euler had found 30 pairs, a number which he later extended to 60. In 1866, 16-year o
I. Paganini found the small amicable pair (1184, 1210) which had eluded his more illustrious predecessors (Paganini 1866-1867; Dickso
There were 390 known amicable pairs as of 1946 (Escott 1946). There are a total of 236 amicable pairs below
Riele 1986), 3340 less than
(Moews and Moews 1993ab), 4316 less than
(Cohen 1970), 1427 b
(Moews and Moews 1996), and 5001 less tha
(Moews and Moews 1996).
Rules for producing amicable pairs include the Thâbit ibn Kurrah rule rediscovered by Fermat and Descartes and extended by Euler to E
further extension not previously noticed was discovered by Borho (1972).
Pomerance (1981) has proved that
for large enough (Guy 1994). No nonfinite lower bound has been proven.
Let an amicable pair be denoted
where
and
.
is called a regular amicable pair of type
if
is the greatest common divisor,
are squarefree, then the number of prime factors of
There are no regular pairs of type
is even, then
and
, and take
for
. If
and
are and . Pairs which are not regular are called irregular or exotic
and
cannot be an amicable pair (Lee 1969). The minimal and maximal values of
found by te Riele (1986) were
te Riele (1986) also found 37 pairs of amicable pairs having the same pair sum. The first such pair is (609928, 686072) and (643336, 65
the pair sum
te Riele (1986) found no amicable -tuples having the same pair sum for
. However, Moews and Moews found a triple in 1993, and
quadruple in 1995. In November 1997, a quintuple and sextuple were discovered. The sextuple is (1953433861918, 2216492794082), (
2201886714184), (1981957651366, 2187969004634), (1993501042130, 2176425613870), (2046897812505, 2123028843495), (20681
2101813493962), all having pair sum 4169926656000. Amazingly, the sextuple is smaller than any known quadruple or quintuple, and i
than any quintuple.
The earliest known odd amicable numbers all were divisible by 3. This led Bratley and McKay (1968) to conjecture that there are no ami
coprime to 6 (Guy 1994, p. 56). However, Battiato and Borho (1988) found a counterexample, and now many amicable pairs are known
divisible by 6 (Pedersen). The smallest known example of this kind is the amicable pair (42262694537514864075544955198125,
42405817271188606697466971841875), each number of which has 32 digits.
A search was then begun for amicable pairs coprime to 30. The first example was found by Y. Kohmoto in 1997, consisting of a pair of n
having 193 digits (Pedersen). Kohmoto subsequently found two other examples, and te Riele and Pedersen used two of Kohmoto's exa
calculated 243 type-
pairs coprime to 30 by means of a method which generates type-
No amicable pairs which are coprime to
pairs from a type-
pairs.
are currently known.
The following table summarizes the largest known amicable pairs discovered in recent years. The largest of these is obtained by definin
then , ,
and
are all primes, and the numbers
are an amicable pair, with each member having
decimal digits (Jobling 2005).
digits date
reference
4829 Oct. 4, 1997
M. García
8684 Jun. 6, 2003
Jobling and Walker 2003
16563 May 12, 2004 Walker et al. 2004
17326 May 12, 2004 Walker et al. 2004
24073 Mar. 10, 2005 Jobling 2005
Amicable pairs in Gaussian integers also exist, for example
and
(T. D. Noe, pers. comm.).
SEE ALSO: Aliquot Sequence, Amicable Quadruple, Amicable Triple, Augmented Amicable Pair, Breeder, Crowd, Euler's Rule, Friendly
Multiamicable Numbers, Pair Sum, Quasiamicable Pair, Rational Amicable Pair, Sociable Numbers, Super Unitary Amicable Pair, Thâbi
Unitary Amicable Pair
220, 284, 1184, 1210, 2620, 2924, 5020, 5564, 6232, 6368, 10744, 10856,
12285, 14595, 17296, 18416, 63020, 66928, 66992, 67095, 69615, 71145,
76084, 79750, 87633, 88730, 100485, 122265, 122368, 123152, 124155,
139815, 141664, 142310 (list; graph; listen; history; internal format)
Greetings from The On-Line Encyclopedia of Integer Sequences!)
A063990 as a simple table:
n
1
2
3
4
5
6
7
a(n)
220
284
1184
1210
2620
2924
5020
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
5564
6232
6368
10744
10856
12285
14595
17296
18416
63020
66928
66992
67095
69615
71145
76084
79750
87633
88730
100485
122265
122368
123152
124155
139815
141664
142310
L’evidenza in rosso dei valori reali è nostra
Distribuzione dei numeri amicabili a(N)) fino a 10^n
TABELLA 1 Logaritmica (Log(N))
N
1
2
3
N =10^n
10
100
1 000
a(N) valori reali
0
0
2
Stima a(N) ≈ n^2
1
4
9
4
5
≈ 5,5
10 000
100 000
142 310
10
26
34
Previsione per N = 1 000 000 = 10^6,
16 ≈ 10
25 ≈ 26
30,25 ≈ 34
6^2 = 36
Previsione per N = 10 000 000 = 10^7, 7^2 = 49
Come possiamo facilmente vedere, i numeri amicabili hanno una
distribuzione, fino a 10^n, di circa n^2, e quindi di circa
a(N) = a(10^n) ≈ (Log N) ^2
con il logaritmo naturale, invece abbiamo trovato che
a(N) = a(10^n) ≈ ½* (ln 10^n-1)^2
(il logaritmo naturale, com’è noto, è circa il doppio del logaritmo
naturale; con valori leggermente in difetto a partire da n = 5.
Per N = 10^6 = 1 000 000, possiamo quindi prevedere una stima di
a(10^6) ≈ 6^2 = 36, col logaritmo decimale e 33 con il
logaritmo naturale (vedi Tabella successiva); valori approssimati
ma attendibili , secondo i relativi grafici:
A063990 as a graph:
TABELLA 2 LOGARITMICA
con il logaritmo naturale , con stima a(10^n) ≈ (½ ln 10^n-1)^2
N
1
2
3
4
5
5,154
6
N =10^n
10
100
1 000
10 000
100 000
(142 560 ≈ 142310)
1 000 000
a(10^n) valori reali
0
0
2
10
26
34
?
Stima logaritmica
0
1,32
5,30
21,20
33.13
35,19
47,71
Previsione per N = 10^6 = 1000 000, a(10^6) ≈ 33,13 ;
previsione per N = 10 000 000, a (10^7) ≈ (½ ln (10^6)^2 ≈ 6,90^2 =
47,71; tali previsioni sono molto vicine ai valori stimati con il Logaritmo
decimale (tabella precedente), rispettivamente
n^2 = 6^2 = 36 ≈ 33
n^2 = 7^2 = 49 ≈ 47
Dimostrazione su Forme 6k -2 e 6k +2 dei numeri amici
Per i numeri perfetti, abbiamo trovato che tranne il 6 iniziale , tutti gli
altri sono di forma 6k – 2, poiché 6 non è della forma aritmetica che da i
numeri perfetti ( (2^n +1 -1) * 2^n ) . Per tutti gli altri, infatti, tale
formula dà numeri di forma 6k-2, poiché 2^n con n dispari dà valori di
6k+2 , per esempio 2^5=32 = 6*5 +2: togliendo 1 abbiamo 6k+1, che deve
essere moltiplicato per 2^n con n pari, di forma 6k -2, cosicché abbiamo:
(6k+1) (6k-2) = 6k^2 -2*6k-2 +6k -2 = 6k(k-2k+k) -2 = 6k – 2,
come si può verificare per tutti i numeri perfetti maggiori di 6; per
esempio, 28 = 6*5-2, 496= 6*83 -2, 8128 = 6*1355 -2 , ecc.
Per i numeri amici, troviamo invece che uno di loro (il più piccolo o il
più grande non importa) è di forma 6k-2 e l’altro è sempre di forma 6k+2,
come si può facilmente verificare:, qui gli esempi per le coppie più piccole:
220 = 6*37 - 2
284 = 6*47 + 2
1184 = 6*591 + 2
1210 = 6*202 - 2
2620 = 6*437 - 2
2924 = 6*487 + 2
…
…
…
…
…
…
17296 = 6*2883 - 2 18416 = 6*3069 + 2
La dimostrazione per i numeri amici di forma 6k-2 è simile a quella per i
numeri perfetti (“amici” di se stessi), solo che per quello di forma 6k+2
c’è certamente qualche cambio di segno + o - che poi determina il segno
finale in + 2, da cui la forma 6k+2 dell’altro numero amico nella stessa
coppia .
Lasciamo ai più volenterosi tale più dettagliata dimostrazione.
Notiamo anche che la somma di due numeri amici è di forma 6k,
poichè, essendo essi di segno discorde, avremo:
6k - 2 + 6k’ +2 = 6k + 6k’ = 6(k + k’)
Per esempio, per 220 = 6*37 – 2 e 284 = 6*47 + 2 con k = 37 e k’ = 47
abbiamo
6*37-2+6*47+2 =220 + 248 = 504 = 6(37 + 47) = 6*84
Per la differenza, invece, l‘avremo di forma 6(k’ - k) + 4= 6(k’- k + 1) - 2
6k+2- (6k’-2) = 6k +2 -6k’ +2 = 6(k’- k) + 4 = 6(k’- k +1) -2
Sempre per 220 e 284, avremo ora:
284 – 220 = 64 = 6*10 + 4, essendo 10 = k’ – k = 47 – 37 = 10
6*47 +2 - 6*37 = 6*10 + 4 = 64 =
6(47 - 37 + 1) - 2 = 6*11 -2 = 66 -2 = 64
Conclusioni
Possiamo concludere dicendo che con questo lavoro sui numeri amici
abbiamo trovato alcune piccole novità, come la loro distribuzione
fino a 10^n, con stima a(N) ≈ n^2, sulla loro forma 6k - 2 oppure 6k + 2
per ognuno dei due numeri di tutte le coppie di numeri amici , ma con
segno discorde; e la dimostrazione della forma 6k -2 dei numeri perfetti
tranne il 6 iniziale (le formule per i numeri perfetti e per i numeri amici
sono, come si è visto, strutturalmente molto simili)
Riferimenti
1) Wikipedia
2) Wolfram Mathworld
3) “Il gioco delle matematiche” del prof. Carmelo Di Stefano, Armando
Editore
Caltanissetta 1.3.2011