Prima prova in itinere del 17/11/2008

ESERCIZIO E1: I diodi D1 e D2 sono ideali. Il segnale di ingresso VIN(t) varia linearmente
nell’intervallo VIN ∈ [0, 40] V. Sapendo che EO = 20 V, R1 = 10 KΩ
Ω; R2 = R3 = 5 KΩ
Ω ; R4 = 15 KΩ
Ω
si determinino e si traccino graficamente le tre relazioni: VOUT = ƒ1(VIN) (4 punti), IO = ƒ2(VIN)
(2 punti) ed I1= ƒ3(VIN) (4 punti). (Prima Prova in Itinere 17 novembre 2008).
Si tratta di un circuito con due diodi D1 e D2, supposti ideali, alimentato da un segnale in tensione
che cresce linearmente da zero a quaranta volt.
I1
Per i due diodi si richiede l’utilizzo del modello
R3
D1
R1
lineare a tratti di prima specie con i due tratti
D2
di caratteristica fra di loro perpendicolari ed
intersecantesi nell’origine degli assi coordinati
R4
R2
V
AK, ID. In sostanza è da considerare nulla sia la
VIN(t)
VOUT(t) tensione di soglia Vγγ, sia la tensione V
DON di
conduzione dei diodi D1 e D2. Una strategia di
IO
EO +
analisi iniziale del circuito è quella di ritenere,
−
contemporaneamente, i due diodi interdetti e
verificare se la rete circuitale che ne deriva è
(figura - 1)
‘elettricamente compatibile’ e coerente con i
valori che nel tempo assume il segnale di ingresso. L’ipotesi relativa ai diodi D1 e D2 entrambi
interdetti conduce a verificare, per ispezione diretta, la validità elettrica o meno della rete di
seguito riportata come figura 1a, in cui i due diodi sono modellati con due interruttori aperti e si
considera inizialmente VIN(t) = 0.
In tali ipotesi, per ispezione diretta della rete, si
K1
A1
evince che non sussiste alcuna maglia chiusa e,
di conseguenza, sono nulle le correnti in ogni
K2 R3
R1
lato della rete; pertanto, se si applica la legge di
A2
Kirchhoff delle tensioni alla maglia contenente
R4
EO, R2, R3 ed R4 si ottiene: VA2K2 − EO = 0, da
R2
+
VOUT cui risulta: VA2K2 = EO > 0, e ciò è in antitesi
VIN = 0
con l’ipotesi iniziale di considerare il diodo D2
−
+
stato di interdizione. Pertanto, si verifica
nello
EO
−
che per VIN(t) = 0 V il diodo D2 si trova nello
stato di conduzione, cioè è ON. La conduzione
di D2 implica l’analisi della rete di figura 1b, in
(figura - 1a)
cui il diodo stesso viene modellato col bipolo
corto circuito mentre D1 è ancora considerato
K1
A1
I1
nello stato di interdizione. Il generatore EO
K2 R3
riparte la propria tensione fra le resistenze R2,
R1
R
3 ed R4 il che rende il potenziale del catodo
A2
VK1 positivo rispetto al potenziale dell’anodo
R4
VA1 e ciò conferma l’ipotesi che il diodo D1 sia
R2
Vα
+
VOUT
effettivamente nello stato di interdizione, cioè
VIN
−
OFF. Si conclude che:
+
I
O
*
EO
∀t : 0 ≤ vin (t ) < vin
(t )
−
D1 è OFF mentre D2 è ON. Il circuito che deve
essere
esaminato, come già detto, è mostrato in
(figura - 1b)
figura 1b nella quale D1 resta modellato con un
circuito aperto. La tensione di uscita vO(t) resta determinata dalla ripartizione della tensione del
generatore indipendente EO operata dal partitore resistivo costituito dalle tre resistenze R2, R3 ed
R4; si ottiene, così, la relazione di seguito riportata:
vo ( t ) =
R4 ⋅ E o
15 ⋅ 20
15 ⋅ 20
=
=
= 12V
R2 + R3 + R4 (5 + 5 + 15)
25
La rete di figura 1b conserva la propria validità
finché il segnale di ingresso VIN non raggiunge il
valore Vα; in tale contesto, infatti, l’applicazione
della legge di Kirchhoff delle tensioni alla maglia
d’ingresso porge la seguente relazione:
VA1K1 − VIN + Vα = 0
A1
R1
VA1K1 = VIN − Vα = 0
K2 R3
A2
+
−
dalla quale si evince che:
I1 α
K1
VIN
Vα
R2
R4
VOUT
+
IO
EO
Appena il segnale di ingresso supera il valore Vα il
−
diodo D1 cambia stato e si porta in conduzione; tale
stato viene garantito dall’aumentare del segnale di
(figura - 1c)
ingresso VIN. Il calcolo della tensione Vα è ottenuto
tramite la relazione esprimente la legge del partitore resistivo di tensione che di seguito si esplicita:
Vα (t ) =
( R3 + R4 ) ⋅ E o (5 + 15) ⋅ 20 20 ⋅ 20 4 ⋅ 20
=
=
=
= (4 ⋅ 4) = 16V
R2 + R3 + R4
(5 + 5 + 15)
25
5
In conclusione si osserva che:
*
∀t : 0 ≤ vin ( t ) < [vin
(t )
Vo (t ) =
= 16V ]
R4 ⋅ E o
= 12V
R2 + R3 + R4
⇒ D1 è OFF mentre D2 è ON
I o (t ) =
Vo (t )
12
=
= 800 µA I1 (t ) = 0
R4
15 ⋅ 103
La rete da esaminare, al crescere di VIN, è mostrata in figura 1c in cui i diodi sono entrambi
modellati da due corto circuiti. Pertanto, si può asserire quanto segue:
*
**
∀t : [v IN
(t ) = 16V ] ≤ vin ( t ) < v IN
(t ) ⇒ D1 è ON e D2 è ON
L’esame del circuito di figura 1c evidenzia una classica rete riconducibile ad una rete a due nodi, la
cui tensione comune di nodo vα(t) è ricavabile con il principio dei potenziali di nodo, noto anche
come principio di Millman. La tensione Vα comune a tutti i lati della rete posti fra loro in
parallelo è, pertanto, definita dalla scrittura che di seguito si esplicita:
[VIN (t ) R1 ] + ( E o R2 )
[VIN (t ) R2 + E o R1 ] ( R1 R2 )
=
=
1
1
1
R2 ( R3 + R4 ) + R1 ( R3 + R4 ) + R1 R2
+
+
R1 R2 ( R3 + R4 )
R1 R2 ( R3 + R4 )
V (t ) R2 + E o R1
R1 R2 ( R3 + R4 )
= IN
⋅
=
R1 R2
( R3 + R4 ) ⋅ ( R1 + R2 ) + R1 R2
R2 ( R3 + R4 ) ⋅ VIN ( t )
R1 ( R3 + R4 ) ⋅ E o
=
+
( R3 + R4 ) ⋅ ( R1 + R2 ) + R1 R2 ( R3 + R4 ) ⋅ ( R1 + R2 ) + R1 R2
Vα (t ) =
Sostituendo i dati forniti dalla traccia si perviene alla relazione seguente:
5 ⋅ (5 + 15) ⋅ VIN (t )
10 ⋅ (5 + 15) ⋅ 20
+
=
(5 + 15) ⋅ (10 + 5) + 10 ⋅ 5 (5 + 15) ⋅ (10 + 5) + 10 ⋅ 5
5 ⋅ 20 ⋅ VIN (t )
10 ⋅ 20 ⋅ 20
100
4000 2
80
=
+
=
⋅ VIN (t ) +
= ⋅ VIN +
(20 ⋅ 15) + 50 (20 ⋅ 15) + 50 350
350 7
7
Vα (t ) =
ovvero:
Vα (t ) =
2
80 2 ⋅ VIN (t ) + 80
⋅ VIN (t ) +
=
[V ]
7
7
7
La tensione di uscita VO(t) richiesta si ottiene applicando la legge del partitore resistivo di tensione
fra le resistenze R4 ed R3; infatti, vale la posizione seguente:
Vo (t ) =
R4
15 2 ⋅ VIN (t ) + 80 3 2 ⋅ VIN (t ) + 80
Vα (t ) =
⋅
= ⋅
R3 + R4
5 + 15
7
4
7
In conclusione si perviene alla cercata relazione:
Vo (t ) =
3
60
⋅ VIN (t ) +
[V ]
14
7
Il legame ottenuto caratterizza una retta con coefficiente angolare m = tagα
α = 3/14. Si osservi che
per VIN(t) = 16V viene riconfermato il valore della tensione d’uscita VO(t) = (16·3/14)+(60/7) = 12V.
La corrente IO(t) è determinata dalla legge di Ohm applicata alla resistenza R4, che è sottoposta alla
tensione VO(t), oppure alla serie delle due resistenze R3 ed R4 facendo ricorso alla tensione Vα(t).
Si relaziona, pertanto, come segue:
Vo (t ) 3 VIN (t )
60
1
4
=
⋅
+
=
⋅
V
(
t
)
+
[ mA] , ed anche:
IN
R4
14 15 ⋅ 103 7 ⋅ 15 ⋅ 103 70
7
V (t )
80
4
 2 V (t )
 −3 1
I o (t ) = α
=  ⋅ IN
+
⋅ VIN (t ) + [mA]
 10 =
R3 + R4  7 (5 + 15) 7 ⋅ (5 + 15) 
70
7
I o (t ) =
Per quanto riguarda il calcolo della corrente I1(t), l’applicazione della legge di Ohm alla resistenza
R1 consente di relazionare come di seguito esplicitato:
VIN (t ) − Vα (t ) VIN (t ) Vα (t )  VIN (t ) 2 ⋅ VIN (t ) + 80 − 3
=
−
=
−
 10
 10

R1
R1
R1
7 ⋅ 10
5
8
=
⋅ VIN (t ) − [mA]
70
7
I1 ( t ) =
La rete di figura 1c conserva la propria validità finché il segnale di ingresso VIN non raggiunge un
**
valore VIN tale da rendere il potenziale Vα del
K1
A1
I1
nodo α uguale alla tensione del generatore EO.
K2 R3
R1
In tale contesto, infatti, la tensione VA2K2 ai capi
A2
del diodo D2 si annulla VA2K2 = 0 per diventare
poi negativa, il che porta il diodo a mutare stato
R4
R2
passando dalla conduzione alla interdizione.
+
VOUT
VIN
Dovrà, quindi, verificarsi la condizione:
−
+
2 **
80
IO
EO
V
(
t
)
=
E
=
⋅
V
(
t
)
+
−
α
o
IN
7
7
dalla quale si determina il valore della tensione
(figura - 1d)
d’ingresso che porta il diodo D2 nello stato OFF.
Eseguendo i necessari passaggi algebrici si ottiene quanto segue:
7 E o − 80 (7 ⋅ 20) − 80 60
2 **
80
**
E o = ⋅VIN
(t ) +
⇒ VIN
(t ) =
=
=
= 30V
7
7
2
2
2
Riassumendo, si perviene alla seguente conclusione:
∀t : [v *IN (t ) = 16V ] ≤ vin (t ) < [v **
IN ( t ) = 30V ]
⇒ D1 è ON e D2 è ON
Per i valori del segnale di ingresso VIN(t) ≥ 30 V, il diodo D2 si apre mentre D1 resta in conduzione.
**
∀t : [VIN
(t ) = 30V ] ≤ Vin (t ) ≤ 40V ] ⇒ D1 è ON e D2 è OFF
Il circuito che dev’essere esaminato è quella mostrata in figura 1d in cui D1 è modellato con il corto
circuito mentre D2 viene modellato da un circuito aperto. Tramite ispezione diretta si osserva che
I1 = IO ed il calcolo della tensione VO(t) è immediato applicando la legge del partitore resistivo di
tensione realizzato dalle tre resistenze R1, R3 ed R4; si ottiene, pertanto:
Vo (t ) =
R4 ⋅ VIN (t )
15 ⋅ VIN (t )
15
1
=
= ⋅ VIN (t ) = ⋅ VIN (t ) [V ]
( R1 + R3 + R4 ) (10 + 5 + 15) 30
2
Il legame ottenuto caratterizza una retta con coefficiente angolare m= tagβ = 1/2. Si osservi che per
VIN(t) = 30V si ottiene VO(t) = 15V, ovvero viene riconfermato il valore della tensione d’uscita dato
dalla relazione: VO(t) = [(3·VIN/14) + (60/7)] = [(3·30/14) + (60/7)] = (210/14) = 15V. Consegue che
la tensione di uscita è una funzione continua e tale sarà anche la transcaratteristica VO = ƒ(VIN).
Per le correnti I1(t) ed IO(t) vale la relazione seguente:
I o ( t ) = I1 ( t ) =
Vo (t ) VIN (t )
VIN (t )
VIN (t )
− 3 VIN ( t )
=
=
=
⋅
10
=
[ mA]
R4
2 R4
30
30
2 ⋅ 15 ⋅ 103
La transcaratteristica vO = ƒ(VIN) è mostrata in figura 1e in cui sono evidenziati per ciascun tratto
della spezzata, che definisce la curva in oggetto, la pendenza e lo stato di conduzione dei diodi.
VO
D1 OFF
D2 ON
D1 ON
D2 ON
D1 ON
D2 OFF
(figura 1e)
20 V
β
15 V
m = tag(β
β) = (1/2)
β = arctag(1/2)
β = 26,56°
α
12 V
30 V
16 V
m = tag(α
α) = (3/14)
α = arctag(3/14)
α = 12,1°
40 V
VIN
In figura 1f, invece, sono evidenziati gli andamenti delle transcaratteristiche relative alle correnti
I1 ed IO. Si osserva che nel terzo tratto, come già confermato dai calcoli, le correnti coincidono.
I1 , IO
D1 OFF
D2 ON
D1 ON
D2 ON
D1 ON
D2 OFF
(figura 1f)
4/3 mA
1 mA
m = tag(ϕ
ϕ) = (5/70)
ϕ = arctag(5/70)
ϕ = 4,08°
δ
γ
800 µA
ϕ
16 V
30 V
m = tag(γγ) = (1/70)
γ = arctag(1/70)
γ = 0,818°
40 V
VIN
m = tag(δ
δ) = (1/30)
δ = arctag(1/30)
δ = 1,91°
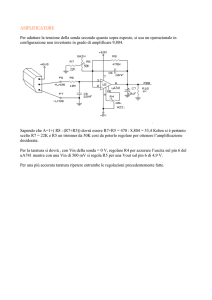
ESERCIZIO E2: Si determini il punto operativo del circuito di figura 2, sapendo che VS è
una sorgente di piccolo segnale. Si indichi la regione di funzionamento del transistore (3 punti).
Si determini il guadagno di piccolo segnale VO/VS nella condizione operativa determinata al
punto precedente (7 punti). Sono noti: EG = 2 V; VT = 1 V; K = 100 µAV−2; RD = 10 KΩ.
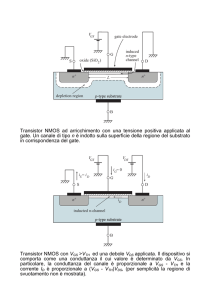
Si tratta di un MOS a canale N polarizzato dal generatore
indipendente stazionario di tensione EG e sottoposto alle
variazioni introdotte dal generatore di piccolo segnale VS.
MN
Ai fini della polarizzazione, atteso che la traccia non indica
RD
la presenza di componente continua associata alla sorgente
V
O
+
di segnale VS, benché non sia presente alcun condensatore
EG
VS
−
atto a funzioni di disaccoppiamento del segnale stesso, si
deve considerare soltanto l’azione del generatore EG. In
sostanza il generatore di segnale VS deve essere spento. La
rete per definizione di punto di riposo Q (punto operativo)
viene, quindi, mostrata in figura 2a nella quale VS è modellato dal bipolo corto circuito. Tramite la
ispezione diretta si evince con immediatezza che il MOS, a canale N, è sicuramente acceso; infatti
si evince: VGS = EG = 2V > VT
Procedendo in una stesura un poco pedissequa, si ipotizza il
(figura - 2a)
MOS
in zona di saturazione e si imposta la corrispondente
ID
relazione costitutiva del dispositivo, esplicitando la
MN
scrittura che di seguito si riporta:
EG
RD
I D = K ⋅ (VGS − VT ) 2 = K ⋅ (VG − VT ) 2 =
VO = VDS
+
−
−6
2
(figura - 2)
∼
= 100 ⋅ 10 (2 − 1) = 100 µA
Applicando la legge di Kirchhoff delle tensioni alla maglia
di uscita del MOS a canale N, si relazione come segue:
VDS = − RD I D = −10 ⋅ 103 ⋅ 100 ⋅ 10 − 6 = −1V
Il risultato conseguito mostra come NON risulti soddisfatta la condizione caratteristica della zona
di saturazione; infatti si ha: VDS < (VGS − VT). Il MOS NON È saturo e poiché è acceso consegue
che esso funziona in zona ohmica; pertanto, la corrente ID dovrà soddisfare la relazione costitutiva
che di seguito si esplicita:
2
I D = K ⋅ [2(VGS − VT ) ⋅ VDS − VDS
] = K ⋅ (VG − VT ) 2
dalla quale, ricordando che VDS = −RD·ID, si ottengono le scritture di seguito riportate:
I D = 2 K (VGS − VT ) ⋅ ( − RD I D ) − K ( − RD I D ) 2
KRD2 I D2 + 2 KRD (VGS − VT ) I D + I D = 0
Sostituendo i dati forniti dalla traccia si ottiene:
2
100 ⋅ 10 − 6 (10 ⋅ 103 ) 2 I D
+ 2 ⋅ 100 ⋅ 10 − 6 ⋅ 10 ⋅ 103 ⋅ (2 − 1) I D + I D = 0 , ovvero:
104 I D2 + 2 I D + I D = 0 ⇒ 104 I D2 + 3I D = 0 ⇒ (104 I D + 3) ⋅ I D = 0
da cui si perviene alle posizioni finali:
ID = 0 A
I D = −3 ⋅ 10 − 4 = −300 µA
L’unica soluzione accettabile dell’equazione di secondo grado, nella variabile corrente di drain ID,
è data da ID = 0 A in quanto una corrente negativa ID = -330 µA implica che il MOS, che deve
essere polarizzato, si comporti come un generatore indipendente di tensione, il che È assurdo.
Atteso che ID = 0A, è immediato concludere che risulta necessariamente anche: VDS = -RD·ID = 0 V.
Pertanto il punto di riposo o punto operativo del MOS a canale N è caratterizzato dalla seguente
terna di grandezze elettriche ai suoi morsetti:
VGS = 2 V; ID = 0A; VDS = 0 V
Si devono, adesso, determinare i parametri dinamici, calcolati nel punto di riposo, specifici della
costituzione del modello del MOS, atto a consentire lo studio del comportamento alle variazioni
dovute all’azione del generatore di piccolo segnale. Nel proseguo si fa riferimento alla
convenzione che, in si esplicita nel seguente modo:
iD = I D + id in cui è: iD = valore istantaneo; ID = valore punto di riposo; id = variazione
v DS = VDS + vds
v GS = VGS + v gs
con: vDS = valore istantaneo; VDS = valore punto di riposo; vds = variazione
con: vGS = valore istantaneo; VGS = valore punto di riposo; vgs = variazione
Il doppio bipolo a parametri G (si ricordi che il MOS è un dispositivo attivo pilotato in tensione)
precipuo di tale modello si caratterizza per le relazioni analitiche costitutive che attingono la loro
origine dalla composizione del differenziale totale della funzione di due variabili iD = ƒ(vGS, vDS),
dato che iG = φ(vGS, vDS) = 0, e che di seguito si riportano:
diG = 0
di D =
∂i D
∂vGS
dvGS +
∂i D
∂v DS
v GS =VGS
v GS =VGS
v DS =V DS
v DS =V DS
Ricordando le posizioni effettuate in ambito teorico e precisamente che:
∂i
gm = D
∂vGS
dv DS
dv DS = vds
dvGS = v gs
di D = id
∂i
gd = D
∂v DS
v GS =VGS
v GS =VGS
v DS =V DS
v DS =V DS
si perviene alla definizione analitica del modello caratteristico del MOS valido alle variazioni dovute
a piccolo segnale; si ottiene infatti con ovvio
D ids
ig = 0 G
significato sia fisico e formale delle indicate
grandezze:
{
Qg : i g = 0 id = gmv gs + gd vds
}
gd
vgs
vds
Il parametro gm noto come transconduttanza
gmvgs
conduttanza diretta, costituisce il parametro
del generatore dipendente di corrente pilotato
S
S
(figura - 2b)
dalla tensione vgs di ingresso con cui l’uscita è
informata dello stato dell’ingresso, mentre il parametro gd assume il significato di conduttanza
d’uscita sentita ai morsetti di drain e di source. Si può procede al calcolo dei parametri dinamici.
2
∂ K ⋅ [2 ⋅ (vGS − VT ) ⋅ v DS − v DS
]
∂i D
gm =
=
=
∂vGS v GS =VGS
∂vGS
v GS =VGS
v DS =V DS
v DS =V DS
= 2 Kv DS vGS =VGS = 2 KVDS = 0 Ω −1
v DS =VDS
∂i
gd = D
∂v DS
v GS =VGS
v DS =V DS
=
{
}
{
}
2
∂ K ⋅ [2 ⋅ (vGS − VT ) ⋅ v DS − v DS
]
∂vGS
, ovvero:
v GS =VGS
v DS =V DS
gd = [2 K (vGS − VT ) − 2v DS ] vGS =VGS = 2 K (VGS − VT ) − 2VDS =
v DS =V DS
−6
= 2 K (VGS − VT ) = 2 ⋅ 100 ⋅ 10 (2 − 1) = 200 ⋅ 10− 6 = 200 µΩ − 1
Atteso quanto premesso, il circuito equivalente dinamico di piccolo segnale è mostrato in figura 2c.
Poiché dal calcolo della transconduttanza gm
si è ottenuto il valore gm = 0 Ω−1, e benché sia,
G
D
come si evince per ispezione diretta vgs = −vs,
i
il
corrispondente generatore pilotato di corrente
ds
gd
vgs
vds
comandato in tensione gmvgs deve considerarsi
gmvgs
spento. Il circuito dinamico sul quale calcolare
S
vO il guadagno di tensione AV = VO/VS è mostrato
RD
in figura 2d.
∼
vS
G
gd
vgs
(figura - 2c)
Sempre per ispezione diretta della figura 2d
si evince che la tensione di uscita è definita
dalla legge del partitore resistivo di tensione
che si realizza fra la resistenza RD di drain e
la conduttanza gd; si ottiene così la relazione
seguente:
vo = − RD ⋅ ids = − RD
D
− vS
RD + (1 gd )
S
∼
ids
vds
RD
vO
vS
(figura - 2d)
Svolgendo i necessari passaggi algebrici si perviene alla scrittura che di seguito si esplicita:
vo = R D
RD ⋅ v S
gd RD
=
⋅ vS
( gd RD + 1) gd (1 + gd RD )
Dalla relazione ora ottenuta, consegue che il guadagno di tensione AV = VO/VS è calcolabile con la
relazione seguente:
vo
gd RD
gd RD
1
200 ⋅ 10 − 6 ⋅ 10 ⋅ 103
AV =
=
⋅ vS ⋅
=
=
=
v S (1 + gd RD )
v S (1 + gd RD ) 1 + (200 ⋅ 10 − 6 ⋅ 10 ⋅ 103 )
−2
=
200 ⋅ 10
1 + (200 ⋅ 10 − 2 )
=
2
2
=
1+ 2 3
ESERCIZIO E3: L’interruttore S di figura 3 si apre e si chiude ciclicamente con periodo di
T = 10 µs di funzionamento. In ogni periodo S è inizialmente chiuso per 0,9·T e poi aperto per il
restante intervallo di tempo. Si supponga che nell’istante di tempo tO = 0 sec. la corrente nello
induttore LO sia nulla. Sapendo che il diodo è ideale, si determini la tensione vO(t) per 0 ≤ t ≤ T
(primo periodo di funzionamento del circuito) (7 punti). Si determini inoltre la tensione vO(t)
per 0 ≤ t ≤ 2T (primi due periodi di funzionamento del circuito) (3 punti). Sono noti: EO = 10 V;
LO = 1 mH; RO = 100 Ω. (Prima Prova in Itinere – 17 novembre 2008).
Si tratta di determinare l’andamento temporale della tensione vO(t) ai morsetti della resistenza RO
che fa parte di una rete che modifica la propria struttura per effetto dello stato dell’interruttore S che
LO
+
−
EO
DO
S
(figura - 3)
RO
VO
si apre e si chiude ciclicamente. Si deve, poi, ricordare
che la corrente che circola nell’induttanza costituisce
una variabile di stato, ovvero la funzione iLO(t) è una
funzione temporalmente continua e, pertanto, priva
di repentine variazioni istantanee del suo valore.
La relazione costitutiva dell’induttanza è espressa dalla
scrittura seguente:
v Lo (t ) = L
di L o (t )
; i Lo (t )
= i Lo (0)
t =0
dt
Appare utile condurre lo studio della rete facendo riferimento agli intervalli in cui l’interruttore S
è dapprima chiuso e poi aperto in quanto si hanno variazioni sostanziali della struttura circuitale di
cui la resistenza RO fa parte.
a) Rete valida per 0 ≤ t < 0,9·T. La rete da esaminare è mostrata in figura 3a in cui l’interruttore S è
chiuso. Il corto circuito effettuato dall’interruttore S
LO
fa si che il diodo DO, supposto ideale, non sia percorso
iO
iLO
da corrente e che l’induttanza LO sia sottoposta alla
vLO
DO
tensione EO dell’omonimo generatore indipendente e
stazionario. In tale contesto si ottengono le relazioni
+
RO
VO
EO
che di seguito si esplicitano:
S
−
(figura - 3a)
vo (t ) = Roio ( t ) = 0V
di (t )
Eo = v Lo (t ) = L L o ; i L o (0) = 0 A
dt
L’andamento temporale della corrente iLO(t), atteso che iLO(0) = 0, è dato dalla relazione seguente:
t
t
Eo
E
Eo ⋅ dt = L0 ⋅ di L o (t ) ⇒ di L o (t ) =
⋅ dt ⇒ ∫ di L o (t ) = ∫ o ⋅ dt
L0
0
0 L0
L’esecuzione delle operazioni di integrazione fornisce l’evoluzione temporale della corrente iLO(t)
che di seguito si esplicita:
t
Eo
Eo t
Eo
i L o (t ) − i L o (0) = ∫
⋅ dt ⇒ i L o (t ) =
⋅t
∫ dt ⇒ i L o (t ) =
L
L
L
0 0
0
0 0
Si tratta di una rampa di pendenza EO/LO, che all’istante TO.= 0,9·T assume il valore:
Eo
10 ⋅ 0,9 ⋅ 10 ⋅ 10 − 6
3
−5
−2
i L o (To ) =
⋅ To =
=
9
⋅
10
⋅
10
=
9
⋅
10
= 90 mA
L0
1 ⋅ 10 − 3
b) Rete valida per 0,9·T ≤ t ≤·T. La rete da esaminare è mostrata in figura 3b in cui l’interruttore S
è aperto ed in tale stato permane per un tempo pari a
LO
iO
iLO
0,1·T = 0,1 µs. Poiché la corrente che transita nella
induttanza non può cambiare istantaneamente il suo
vLO
DO
valore, nel diodo DO viene iniettata la corrente iL(t);
+
diodo, per tanto, è polarizzato direttamente e può
il
R
V
O
EO
O
S
−
essere modellato con un corto circuito. Si tratta di
una rete LR nella quale l’andamento temporale della
corrente iLO(t) = iO(t), di tipo esponenziale, risulta
(figura - 3b)
determinato dalla seguente relazione caratteristica:
i L o (t ) = i L o ( ∞) − [i L o ( ∞) − i L o (To )] ⋅ e− ( t − To ) τ in cui è: τ = LO/RO.
Il valore della corrente iLO(∞) si determina considerando che l’induttanza si sia completamente
caricata e che, quindi, sia modellata da un corto circuito; ne consegue che:
i L o ( ∞) = ( E o Ro ) = (10 100) = 0,1 = 100 mA con i L o (To ) = 90 mA
Il calcolo della costante di tempo τ è fornito dalla già citata relazione:
τ = ( Lo Ro ) = (1 ⋅ 10 − 3 100) = 10 − 5 = 10 ⋅ 10 − 6 = 10 µs
Per quanto attiene l’andamento temporale della corrente iLO(t) nell’induttanza LO si ottiene:
( t − 9 ⋅10 − 6 )
( t − 9 ⋅10 − 6 )
−
−
−6
−6
i L o (t ) = 100 − [100 − 90] ⋅ e 10⋅10
= 100 − 10 ⋅ e 10⋅10
[mA]
ed in particolare, si determina il valore della corrente all’istante t = T in cui l’interruttore S si riporta
nello stato di chiusura ottenendo:
( T − 9 ⋅10 − 6 )
(10 − 9 ) ⋅10 − 6
−
−
−6
−6
i L o (T ) = 100 − [100 − 90] ⋅ e 10⋅10
= 100 − 10 ⋅ e 10⋅10
=
− 0,1
= 100 − 10 ⋅ e
= 100 − 9,05 = 90,95 mA
Nota la corrente iLO(t), l’evoluzione temporale della tensione vO(t) ai capi della resistenza RO è data
dalla legge di Ohm; atteso infatti che iO(t) = iLO(t), si ottiene di conseguenza la relazione seguente:
−6
−6
vLo (t ) = Ro ⋅ io (t ) = Ro ⋅ iL o (t ) = 100 ⋅ [100 − 10 ⋅ e −(t −9⋅10 ) (10⋅10 ) ] =
−6
−6
= 10 − e −(t −9⋅10 ) (10⋅10 ) [V ]
Inoltre si verifica che:
v Lo (T ) = Roi L o (T ) = 100 ⋅ 90,95 ⋅ 10− 3 = 9,095 [V ]
c) Rete valida per T ≤ t < 1,9·T. La rete da esaminare è mostrata in figura 3c in cui l’interruttore S
è chiuso e l’induttanza Lo si trova caricata al valore
LO
iO
iLO
iLO(T) = 90,95 mA e sottoposta alla tensione costante
del generatore EO. Pertanto si avrà ancora iO(t) = 0 A
vLO
DO
e si verificherà nuovamente un effetto d’integrazione
+
nel
tempo esprimibile con la seguente relazione:
RO
VO
EO
S
−
t
E
i L o (t ) − i L o (T ) = ∫ o ⋅ dt
T L0
(figura - 3c)
Procedendo all’operazione di integrazione si ottiene:
i L o (t ) − i L o (T ) =
Eo
E
(t − T ) ⇒ i L o (t ) = i L o (T ) + o (t − T )
L0
L0
In particolare, effettuando i necessari calcoli, si ottiene quanto di seguito esplicitato:
−6
Eo
− 3 10 ⋅ 0,9 ⋅ 10 ⋅ 10
i L o (1,9T ) = i L o (T ) +
⋅ (1,9T − T ) = 90,95 ⋅ 10 +
=
L0
10 − 3
= 90,95 ⋅ 10 − 3 + 9 ⋅ 10 − 5 ⋅ 10 3 = (90,95 + 90) ⋅ 10 − 3 = 180,95 mA
Dalla condizione iO(t) = 0 A si perviene di nuovo alla conclusione che vO(t) = RO·iO(t) = 0 V.
d) Rete valida per 1,9·T ≤ t < 2·T. La rete da esaminare è mostrata in figura 3d in cui l’interruttore
S è di nuovo aperto, il diodo DO in stato di conduzione e la resistenza RO percorsa dalla corrente
iO(t) = iLO(t). In sostanza si riproducono le stesse condizioni circuitali esaminate in precedenza al
caso b) relativo all’intervallo di tempo 0,9·T ≤ t < T.
La tensione vO(t) ai morsetti della resistenza RO è data
legge di Ohm, tenendo conto che resistenza ed
dalla
DO
vLO
induttanza sono percorse dalla stessa corrente; si deve,
+
pertanto,
concludere che VO(t) = RO iO(t) = RO·iLO(t).
R
VO
O
EO
S
−
Si tratta di una tipica rete LR nella quale l’andamento
nel tempo della corrente nell’induttore iLO(t) = iO(t),
è di tipo esponenziale ed è definito dalla relazione
(figura - 3d)
caratteristica già utilizzata e che di seguito si riporta:
i L o (t ) = i L o ( ∞) − [i L o ( ∞) − i L o (To )] ⋅ e− ( t − To ) τ
in cui, in questo caso, deve intendersi: TO = 1,9·T = 19 µs, iLO(TO) = iLO(1,9T) = 180,95 mA,
mentre, ovviamente, è ancora: τ = LO/RO = 10 µs.
Il valore della corrente iLO(∞) si determina asserendo che l’induttanza si sia completamente caricata
e che, quindi, sia modellata da un corto circuito; stante la rete di figura 3d, di nuovo consegue che:
iLO
LO
iO
i L o ( ∞) = ( E o Ro ) = (10 100) = 0,1 = 100 mA
Per quanto attiene l’andamento temporale della corrente iLO(t) nell’induttanza LO si ottiene:
( t −19 ⋅10 − 6 )
( t −19 ⋅10 − 6 )
−
−
−6
−6
i L o (t ) = 100 − [100 − 180,95] ⋅ e 10⋅10
= 100 + 80,95 ⋅ e 10⋅10
mA
in particolare, si determina il valore della corrente all’istante t = 2·T in cui l’interruttore S si
riporterà nello stato di chiusura ottenendo:
( 2 T −19 ⋅10 − 6 )
( 20 −19 ) ⋅10 − 6
−
−
−6
10⋅10 − 6
i L o (2T ) = 100 + 80,95 ⋅ e
= 100 + 80,95 ⋅ e 10⋅10
=
− 0,1
= 100 + 80,95 ⋅ e
= 100 + 73,25 = 173,25 mA
Nota la corrente iLO(t), l’evoluzione temporale della tensione vO(t) ai capi della resistenza RO sarà
determinata dalla seguente scrittura:
−6
−5
v Lo (t ) = Roio (t ) = Roi L o (t ) = 100 ⋅ [100 + 80,95e − ( t −19 ⋅10 ) (10 ) ] ⋅ 10 − 3
− ( t − 19 ⋅10 − 6 ) (10⋅10 − 6 )
= 10 − e
Inoltre si verifica che:
[V ]
v Lo ( 2T ) = Roi L o ( 2T ) = 100 ⋅ 173,25 ⋅ 10 − 3 = 17,325 [V ]
Nella figura a lato viene mostrata l’espansione del
grafico della tensione vO(t) relativamente allo
intervallo 0,9·T < t < T. Atteso che la costante di
tempo τ è dieci volte più grande dell’intervallo in
esame, l’andamento esponenziale di carica appare
coincidere con una retta. La rete RL, pertanto, si
comporta come un integratore.
Nella figura 3e e figura 3f vengono mostrati gli
andamenti temporali della corrente iLO(t) nella
induttanza LO e della tensione vO(t) ai morsetti
della resistenza RO. Quanto detto per la tensione
vO(t), nell’intervallo 0,9·T < t < T, vale anche per
la corrente iLO(t). Similmente per 1,9·T < t < 2·T.
(figura 3e – Evoluzione temporale della corrente iLO(t) nell’induttanza LO)
(figura 3f – Evoluzione temporale della tensione vO(t) ai morsetti della resistenza RO)