Distribuzioni di variabili aleatorie
Argomenti
Variabili aleatorie discrete e continue, Distribuzione
Normale, Distribuzione Normale Standardizzata
1
Concetti di base
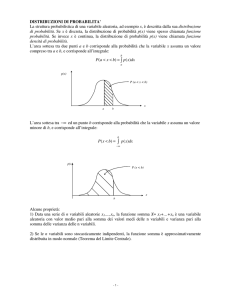
DISTRIBUZIONE DI PROBABILITA’.
Modello matematico che collega i valori di una variabile alle probabilità che tali
valori possano essere osservati. Le variabili casuali (o aleatorie) che osserviamo
possono essere:
• DISCRETE: possono assumere un numero finito o un’infinità numerabile di valori
Processo di conteggio
• CONTINUE: possono assumere un qualsiasi valore reale all’interno di un certo
intervallo di estremi finiti o infiniti
Processo di misurazione
2
Variabile aleatoria discreta
La distribuzione di probabilità di una v.a. discreta è rappresentata dall’elenco
dei valori che la variabile può assumere a cui viene associata la relativa
probabilità di verificarsi.
FUNZIONE DI PROBABILITA’
P ( X xi ) P ( xi )
con
P ( xi ) [0;1]
n
P( x ) 1
i 1
i
FUNZIONE DI RIPARTIZIONE
Fornisce la probabilità che la v.a. X assuma valori ≤ ad un particolare valore xi
i
F ( x) P( X xi ) P( xk )
k 1
3
Variabile aleatoria continua
Per quanto riguarda le variabili aleatorie continue si può
determinare la probabilità che esse assumano valori compresi in
un intervallo.
La probabilità che la variabile assuma un particolare valore è pari
a zero
Non si parla più di funzione di probabilità, ma di funzione di
densità
Proprietà della funzione di densità
Funzione di ripartizione
f ( x) 0 x
f ( x)dx 1
x
F ( x) P( X x)
f ( y )dy
4
Media e varianza delle variabili aleatorie
La media (μ) e la varianza (σ) di una variabile aleatoria X sono i
parametri più importanti della distribuzione di probabilità di X, in
quanto rappresentativi della tendenza centrale e della variabilità
della variabile.
DISCRETA
CONTINUA
n
xf ( x)dx
xi p ( xi )
i 1
D
n
( xi ) p ( xi )
2
2
i 1
2 ( xi ) 2 f ( x)dx
D
5
La distribuzione Normale
La distribuzione normale (o Gaussiana) è la distribuzione continua
più utilizzata in statistica.
Le sue proprietà principali sono:
1. ha forma campanulare
2. le sue misure di posizione centrale (media, mediana e moda)
coincidono
3. ha due punti di flesso in μ-σ e in μ+σ
4. assume valori compresi tra -∞ e +∞
5. ha come asintoto orizzontale l’asse delle ascisse
lim f ( x) lim f ( x) 0
x
x
6
La distribuzione Normale
La funzione di densità di probabilità della normale è data dalla
seguente espressione:
1
f ( x)
e
2
1 x
2
2
Dove:
e = costante matematica (Nepero) approssimata a 2,21828
π = costante matematica approssimata a 3,14159
μ = valore atteso della popolazione
σ = scarto quadratico medio della popolazione
x = valori assunti dalla variabile aleatoria
7
La distribuzione Normale
Essendo e e π delle costanti matematiche, le probabilità di una
distribuzione normale dipendono soltanto dai valori dei due
parametri μ e σ. Diverse combinazioni di questi parametri danno
luogo a differenti distribuzioni normali.
8
La distribuzione Normale
Distribuzione normale al variare di μ.
Distribuzione normale al variare di σ.
9
La distribuzione Normale
Gli intervalli tipici di scarto sono i seguenti:
P( x ) 0, 6827
P( 1,96 x 1,96 ) 0,95
P( 2 x 2 ) 0,9545
P( 2,58 x 2,58 ) 0,99
P( 3 x 3 ) 0,9973
10
La distribuzione Normale
Esempio.
Il tempo medio di permanenza in un ospedale per anziani è di 38 giorni con
uno scarto quadratico medio di 12 giorni. La distribuzione dei tempi di
permanenza è una normale.
Sappiamo quindi che il 68,27% degli ospiti resta in ospedale tra 26 e 50 giorni
38 12 50
38 12 26
La probabilità che un ospite resti 62 giorni è del 2,275%, infatti:
n 62
50 n 12 62 n 2
la coda a destra μ+2σ di in una distribuzione Normale sottende un area di
0,02275.
11
La distribuzione Normale
La funzione di ripartizione di una Normale è data da:
x
1
F ( x) P( X x)
2
e
1 y
2
2
dy
Funzione di ripartizione
per
una
distribuzione
Normale con media pari a
2 e deviazione standard
pari a 1
Funzione di ripartizione per N(2;1)
1,2
1
0,8
0,6
0,4
0,2
0
-2
-1
0
1
2
3
4
5
6
7
12
Distribuzione Normale Standardizzata
L’utilizzo delle funzioni di densità per il calcolo di probabilità relative
ad una v.a. con distribuzione Normale è complesso. Per questo motivo si
ricorre all’impiego di tavole in grado di fornirci le probabilità
desiderate.
Visto che il numero di combinazioni tra μ e σ è infinito conviene far uso
di una trasformazione lineare in grado di standardizzare la generica v.a.
normale per poi ricavare le probabilità dalle tavole della distribuzione
Normale Standardizzata.
La variabile aleatoria standardizzata Z ha valore atteso nullo e scarto
quadratico medio unitario. La sua funzione di densità è:
1 12 Z 2
f ( z)
e
2
13
Distribuzione Normale Standardizzata
STANDARDIZZAZIONE
Consideriamo Z come la variabile ottenuta sottraendo ad X il suo valore atteso e
rapportando il risultato alla deviazione standard
Z
X
14
Distribuzione Normale Standardizzata
Tavola dei valori di
una Normale
Standardizzata
15
Esempi
ESEMPIO 1.
Supponiamo che il tempo necessario per caricare la homepage del
sito Unica sia distribuito normalmente con μ=7 secondi e σ=2
secondi. A ciascun valore della variabile X (tempo di caricamento) è
associato il corrispondente valore della variabile standardizzata Z.
16
Esempi
Supponiamo di voler determinare la probabilità che il tempo di caricamento
della homepage sia inferiore ai 9 secondi. (P(X<9))
Il primo passo è quello di riportare il valore di X=9 secondi al valore della Z
standardizzandolo:
Z
X
97
1
2
Infine si utilizza la tavola dei valori per determinare l’area cumulata fino al
valore Z=1
17
Esempi
Ricaviamo allo stesso modo le seguenti probabilità:
• P(X<7 o X>9)
•P(5<X<9)
18
Esempi
La tavola dei valori della distribuzione Normale Standard è stata fin qui
utilizzata per calcolare l’area sottesa dalla funzione di densità fino ad un
certo valore della v.a. X.
In molti casi (ad esempio in una logica VaR) si è interessati al procedimento
opposto, ossia determinare il valore della v.a X a cui corrisponde una certa
probabilità cumulata.
Supponiamo di voler calcolare il tempo massimo di caricamento per almeno il
10% delle sessioni.
Primo passo è quello di cercare nella tavola dei valori un un’area cumulata il
più vicino possibile allo 0,1 e da questo ricavare il valore di Z.
Z = -1,28
19
Esempi
Il secondo passo consiste nel ricavare il valore di X invertendo la relazione che
abbiamo precedentemente utilizzato per la standardizzazione
X Z
7 (1, 28) 2 4, 44
20
Esempi
Supponiamo (ancora) di voler trovare i valori estremi dell’intervallo
centrato sulla media a cui appartiene il 95% delle osservazioni.
X 7 (1,96) 2 10,92 sec
X 7 (1,96) 2 3,08 sec
21
Esercizio
ESERCIZIO 1.
Il responsabile dell’assemblaggio in una società che fabbrica automobili si
propone di ridurne il tempo necessario. Nell’attuale processo i lavoratori sono
addestrati individualmente. Dopo aver raccolto informazioni il responsabile
stabilisce che il tempo di assemblaggio segue approssimativamente una
distribuzione normale con valore atteso pari a 75 secondi e scarto quadratico
medio pari a 6 secondi.
a) Supponiamo che il responsabile dell’assemblaggio voglia determinare la
probabilità che un addetto scelto a caso impieghi un tempo compreso fra 75 ed
81 secondi per assemblare il pezzo. Come si procede?
b) Qual è la probabilità che un addetto selezionato a caso impieghi al massimo
81 secondi per completare il lavoro? In questo caso guardo la tavola delle
probabilità cumulate.
c) Quanto tempo deve passare perché il 10% degli addetti abbia completato
l’assemblaggio?
[Risultati a)=0,3413 ; b)=0,8413 ; c)=67,32]
22
Distribuzione di Poisson
La distribuzione di Poisson è anche detta distribuzione degli eventi rari. Se
abbiamo un evento E, magari relativo a verificarsi di una specifica perdita
operativa, il numero di volte che E si verifica è una variabile aleatoria
discreta.
Una variabile aleatoria X (numero di volte che si verifica E), che può
assumere i valori 0,1,2,…, è detta variabile aleatoria di Poisson con
parametro λ se la sua distribuzione di probabilità per λ>0 è:
e x
P( X )
x!
Dove:
λ
x
x!
parametro della Poisson
numero di volte che si verifica l’evento E
fattoriale di x (es. se x=4 allora x!=4*3*2*1=24)
23
Distribuzione di Poisson
Una delle caratteristiche principali della variabile aleatoria di Poisson è che il
suo valore atteso e la sua varianza coincidono e sono uguali al parametro λ
della distribuzione.
In base al valore
assunto dal
parametro λ la
distribuzione
acquisisce
differenti forme
24
Distribuzione di Poisson
Esercizio
Ad una guardia medica arrivano in media 3,5 richieste ogni ora di interventi
urgenti a domicilio. Calcolare la probabilità che in una stessa ora arrivino 3, 4,
oppure 5 chiamate urgenti. Il fenomeno può essere descritto utilizzando la
formula di Poisson, con λ = 3,5. Si ha:
e 3,5 3,53
P (3)
0, 2158
3!
e 3,5 3,54
P (4)
0,1888
4!
e 3,5 3,55
P (5)
0,1322
5!
25
Distribuzione di Poisson
Esercizio
Supponiamo che il numero di errori tipografici di una singola pagina del libro
di testo abbia una distribuzione di Poisson di parametro λ=1/2. Calcolare la
probabilità che in una pagina ci sia almeno un errore:
e1 2 1 20
P( X 1) 1 P(0) 1
e1 2 0,3935
0!
26
Distribuzione di Poisson – Tavole -
27
Distribuzione di Poisson – Tavole -
28
Distribuzione di Poisson – Tavole -
29
Distribuzione di Poisson – Tavole -
30
Distribuzione Lognormale
Si dice che una variabile aleatoria X segue una distribuzione log-normale
quando Y=ln(X) segue una distribuzione normale. Si ha quindi per Y la
seguente funzione di densità:
f (Y )
1
Y 2
e
1 ln x Y
2 Y
Dove:
2
Y2 ln x 1
x
1
Y ln x Y2
2
31
Distribuzione Lognormale
Analizziamo l’andamento della funzione di densità di una lognormale con
deviazione standard pari a 2 al variare della media.
32
Distribuzione Lognormale
Analizziamo l’andamento della funzione di densità di una lognormale con
media pari a 2 al variare della deviazione standard.
33
Distribuzione Lognormale
Con la distribuzione Lognormale si possono modellizzare gli importi delle
perdite operative semplicemente basandoci sulla media e la varianza desunte
dai dati storici. Una volta ottenuti i parametri della distribuzione possiamo
ragionare nell’ottica del VaR per determinare qual è l’importo massimo di
una perdita con un certo livello di confidenza.
Esempio
Ipotizziamo di avere la seguente situazione; una banca vuole determinare il
VaR ad un livello di confidenza del 97,5% relativamente all’importo delle
perdite operative dovute ad episodi di frode interna compiute dai suoi
dipendenti. La banca sa che frodi di questo genere si distribuiscono secondo
una lognormale e hanno un impatto medio di 2500 euro e una deviazione
standard di 1875 euro. I passaggi per trovare il VaR sono:
1. abbiamo i parametri μx e σx (della variabile X distribuita lognormalmente)
2. troviamo con questi parametri μY e σY (della variabile Y=lnX distribuita normalmente)
3. troviamo il valore di Y=lnX corrispondente al 97,5% con la normale standardizzata
4. ricaviamo il corrispondente valore della perdita X facendo X=exp(Y)
34
Distribuzione Lognormale
I parametri della lognormale sono:
x 2500
x 1875
Per trovare il VaR al 97,5% dobbiamo riportare la distribuzione Lognormale ad
una distribuzione Normale sulla quale siamo in grado di individuare il valore
corrispondente al livello di confidenza desiderato. Sappiamo che se X si
distribuisce lognormalmente ci sarà una Y=lnX che si distribuisce
normalmente con media pari a μY e varianza pari a σY. Dove:
2
2
1875
2
x
Y ln 1 ln
1 0, 4463
x
2500
1
Y ln x Y2 ln(2500) 0,5 0, 4463 7, 6009
2
35
Distribuzione Lognormale
Adesso dobbiamo trovare il valore, con un intervallo di confidenza del 97,5%, della
variabile Y che si distribuisce come una Normale con media pari a 7,6009 e varianza
pari a 0,4463 (ossia con SQM pari a 0,6680).
Il valore di Y lo troviamo utilizzando la standardizzazione della Normale, come fatto
nella scorsa lezione. Vi ricordo che il valore di Z corrispondente ad un livello di
confidenza del 97,5% è 1,96.
Y Z
7, 6009 (1,96) 0, 6680 8,910275
Nell’ultimo passaggio noi dobbiamo convertire Y=lnX (dove X rappresenta l’importo
della perdita).
Y ln X X exp(Y ) exp(8,910275) 7407, 698
Questa cifra è il nostro VaR al 97,5%.
36