LA LUCE
OTTICA
• OTTICA FISICA: si occupa della natura
ondulatoria della luce, quindi di fenomeni
quali interferenza, diffrazione e polarizzazione
• OTTICA GEOMETRICA: si ignora il
carattere ondulatorio della luce e si parla di
raggi luminosi che si propagano in linea retta,
quindi di fenomeni quali riflessione e
rifrazione
La propagazione rettilinea
della luce: ombra e penombra
• Una sorgente luminosa può essere
Puntiforme o Estesa. Da essa partono i fasci
di raggi di luce, che possono essere intercettati
da un corpo. Se esso arresta completamente il
cammino della luce si dirà Opaco, altrimenti
sarà detto Trasparente.
La propagazione rettilinea
della luce
• Solitamente una sorgente luminosa qualsiasi
emette un fascio di raggi divergenti, cioè essi
costituiranno un cono di luce come in figura
La propagazione rettilinea
della luce: ombra
• Supponiamo di proiettare su uno schermo la luce
proveniente da una sorgente puntiforme e di
frapporre un corpo opaco: sullo schermo
otterremo l’ombra dell’oggetto dai contorni ben
delineati
La propagazione rettilinea
della luce: ombra e penombra
• Se invece di considerare una sorgente puntiforme
consideriamo una sorgente estesa, ma minore del
corpo opaco, si determinano sullo schermo delle
zone di penombra, cioè i contorni della zona
d'ombra sullo schermo non sono ben delineati e si
passa gradualmente dall'ombra alla luce piena.
La propagazione rettilinea
della luce: ombra e penombra
• Se, invece, la sorgente luminosa è più estesa del
corpo, l'ombra è convergente
• Al di là del vertice P non c'è più alcuna ombra
Questo spiega anche il
fenomeno delle ECLISSI. In tal
caso la sorgente S è il sole, il
corpo opaco C può essere la
terra, nel caso delle eclissi di
luna, oppure la luna nel caso
delle eclissi di sole.
La velocità della luce
• L'esperimento che tentò Galileo fu quello di porre
due persone l'una di fronte all'altra munite di due
lumi. La prima persona scopre il proprio lume, la
seconda esegue la medesima operazione non appena
scorge il segnale. In tal modo la prima persona
avrebbe dovuto avere la possibilità di misurare il
tempo necessario alla luce per compiere il percorso
di andata e ritorno. Ma tale velocità era veramente
troppo grande per poter essere apprezzata su
distanze terrestri, cosicché l'esperimento, pur se
ripetuto ponendo le persone a distanza di due o tre
miglia, non diede alcun risultato.
La velocità della luce
• Distanze di tale ordine di grandezza intervengono
nelle osservazioni astronomiche, e fu proprio grazie
al contributo del danese Romer (1644 - 1710), e dei
suoi studi sulle eclissi dei satelliti di Giove che si
ebbe la possibilità di ottenere una stima
sufficientemente precisa della velocità della luce.
La velocità della luce
ROMER
• Iniziamo la prima osservazione dell'eclissi quando la
posizione dei vari astri è come quella descritta in
figura
La velocità della luce
ROMER
• Dall'analisi dei tempi di rivoluzione si calcola che la
seconda eclissi dovrebbe osservarsi esattamente
dopo sei mesi. In effetti l'osservazione avviene con
un ritardo di tempo
. Ciò è dovuto alla nuova
posizione della terra
• Per poter osservare la seconda eclissi la luce
dovrà percorrere un tratto più lungo per
raggiungere la terra: la differenza di lunghezza
dei due percorsi è , pari al diametro dell'orbita
terrestre. Il ritardo di osservazione sarà pertanto:
dove C è la velocità della luce. Da ciò si ricava:
• Romer misurando un ritardo
di
,
noto il valore , ricavò per la luce una velocità
pari a:
• Successivi esperimenti più precisi gli consentirono
di approssimare il valore a
La velocità della luce
FIZEAU
• Fizeau utilizzò uno strumento così composto:
una sorgente luminosa, uno specchio ed una
ruota dentata posta fra di essi
• Il raggio di luce parte dalla sorgente e passando
attraverso uno spazio vuoto della ruota dentata
raggiunge lo specchio, viene riflesso e ritorna al
punto di partenza. Se la luce riflessa viene
intercettata da un dente, vuol dire che il tempo
impiegato dalla luce per percorrere due volte
(andata e ritorno) la distanza ruota-specchio è
uguale al tempo impiegato dalla
ruota a percorrere l'angolo
,
fra il centro di un faro e il centro
di un dente.
La velocità della luce
FOUCAULT
• L'esperienza fu migliorata da Foucault, il
quale anziché una ruota dentata utilizzò uno
specchietto rotante.
• Il raggio parte da S e viene riflesso dallo
specchio rotante, raggiunge il secondo specchio
e viene nuovamente riflesso dallo specchio
rotante, che nel frattempo avrà compiuto una
rotazione pari a un angolo
Dunque il raggio partito dal punto A sarà
proiettato sul punto B. La distanza fra A e B
consente di ottenere l'angolo e se è nota
, si
ottiene il valore di
, che è il tempo impiegato
dalla luce per percorrere la distanza fra i due
specchi per due volte.
• Con questo metodo Foucault ottenne un
valore per C pari a:
• Altre esperienze condotte da Michelson agli
inizi del secolo utilizzando gli stessi
strumenti di Foucault, diedero un valore:
Intensità luminosa e
d'illuminazione
• L'intensità luminosa è la quantità di energia
che un corpo irradia in un secondo (Pertanto
essa è misurata in Watt).
• L'intensità di illuminazione misura la quantità
di energia che arriva su una superficie di un
metro quadro a causa dell'illuminazione
(Essa sarà misurata in
).
RIFLESSIONE
• La riflessione della luce verifica la seguente legge
sperimentale, nota sotto il nome di Legge di SnelliusCartesio:
1) Il raggio incidente, la normale alla superficie
riflettente nel punto di incidenza ed il raggio riflesso
giacciono sullo stesso piano;
2) L'angolo di incidenza è uguale all'angolo di
riflessione.
Diffusione
• Se la luce viene proiettata su una superficie non
levigata, assistiamo al fenomeno della diffusione. La
superficie scabra su cui si proietta il fascio luminoso
può essere approssimata microscopicamente con una
spezzata composta da tanti segmentini ognuno piano.
I raggi, colpendo i segmentini, vengono riflessi
secondo le leggi della riflessione, ma globalmente il
fascio non viene deviato uniformemente ma diffuso
in tante direzioni
SPECCHI PIANI
• IMMAGINE REALE: La luce passa
effettivamente attraverso il punto
immagine e diverge da esso.
• IMMAGINE VIRTUALE: La luce si
comporta come se provenisse dal punto
immagine, sebbene non passi per tale
punto.
SPECCHI PIANI
IMMAGINE
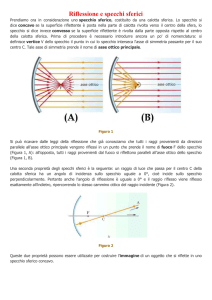
SPECCHI SFERICI
Una superficie riflettente a forma di calotta sferica sarà
da noi chiamato specchio sferico
Se la superficie riflettente è interna alla calotta, parleremo
di specchio concavo; se è esterna, di specchio convesso.
SPECCHI SFERICI
CONCAVI
Il centro della sfera cui la calotta riflettente appartiene
viene chiamato centro di curvatura. L'asse di simmetria
della calotta che passa per il centro di curvatura, si
chiama asse ottico principale, mentre ogni altra retta per
il centro di curvatura che incontra la superficie riflettente
si chiama asse secondario.
L'angolo di apertura è invece l'angolo compreso fra due
rette che passano per il centro di curvatura e sono
tangenti al bordo della calotta.
Costruzione dell'immagine di
un oggetto puntiforme
• Un raggio che parte dalla sorgente S posta ad
esempio sull'asse ottico principale, sarà riflesso in
modo che, rispetto alla normale relativa al punto
(raggio), l'angolo di incidenza è uguale all'angolo di
riflessione. Il raggio incidente viene riflesso in modo
da intersecare l'asse principale nel punto S'.
I punti S ed S' che si
individuano in
questo modo
costituiscono una
coppia di punti
coniugati.
• Consideriamo ora un fascio di raggi tutti
paralleli all'asse principale. Mediante la
costruzione geometrica essi sono riflessi in
modo da intersecare l'asse principale nello
stesso punto F che prende il nome di Fuoco
• Se poniamo una sorgente luminosa nel fuoco di uno
specchio concavo, i raggi saranno riflessi tutti
parallelamente all'asse principale e il punto
coniugato di F sarà all'infinito.
Il fuoco è il punto coniugato del punto all'infinito.
• Il fuoco di uno specchio concavo viene a trovarsi,
con buona approssimazione, a metà fra il centro C e
la superficie riflettente.
La distanza focale f=r/2
dove r è il raggio della sfera cui la calotta riflettente
appartiene.
• se l'oggetto viene posto ad una distanza minore di
quella focale (p<f), i raggi riflessi sono divergenti
e l'immagine appare al di là della superficie
riflettente, poiché essa si determina come il punto
di intersezione del prolungamento dei raggi
riflessi. Diremo in tal caso che l'immagine è
virtuale.
Costruzione dell'immagine di un
oggetto esteso
• Si considerano di solito i seguenti raggi:
– 1) quello parallelo all'asse principale, il cui
raggio riflesso passa per il fuoco dello
specchio;
– 2) quello che passa per il fuoco principale,
che sarà riflesso parallelamente all'asse
principale;
– 3) quello che passa per il centro, che in
quanto coincidente con la normale, verrà
riflesso su sé stesso.
• Situazione 1: oggetto posto ad una
distanza maggiore di 2f, pertanto oltre il
centro (p>2f=R).
L'oggetto appare rimpicciolito e capovolto, tra
il fuoco ed il centro
• Situazione 2: oggetto posto ad una distanza pari
a 2f nel centro (p=2f=R).
L'immagine ha le stesse dimensioni
dell'oggetto, anch'essa nel centro ma capovolta
• Situazione 3: oggetto tra il fuoco ed il centro
(p<2f=R).
L'immagine è capovolta ed ingrandita, posta ad
una distanza maggiore di 2f (q>2f).
• Situazione 4: oggetto nel piano focale (p=f=R/2).
L'immagine risulta ingrandita al massimo,
all'infinito.
• Situazione 5: oggetto tra lo specchio e il fuoco
(p<f).
L'immagine è virtuale: appare al di là dello
specchio, diritta e ingrandita.
Approssimazioni di Gauss
• Quanto descritto vale per specchi sferici che
soddisfano approssimativamente le seguenti
condizioni:
1) angolo di apertura piccolo, cioè la sfera
che contiene la calotta speculare è molto
estesa rispetto ad essa.
2) raggi parassiali, i raggi luminosi
formano con l'asse ottico angoli molto
piccoli.
Relazioni fra punti coniugati
C
V
Per le leggi della riflessione SAC=CAS’
La bisettrice di un angolo interno di un triangolo divide il lato
opposto in parti proporzionali agli altri due lati. Applicando
questa regola al triangolo SAS', se ne ricava:
Relazioni fra punti coniugati
C
V
Poiché stiamo supponendo valide le approssimazioni di Gauss,
esse ci consentono di utilizzare le seguenti espressioni
approssimate: AS = VS ; AS’=VS’ Sostituendo si ottiene:
Relazioni fra punti coniugati
C
V
VS=p ; VS’=q ; SC=p-R ; CS’=R-q Sostituendo in
si ottiene:
Relazioni fra punti coniugati
C
V
Facendo denominatore comune pR-pq=pq-qR
pR+qR=2pq e dividendo per pqR si ottiene:
ma f=R/2
Osservazioni sull’equazione dei
punti coniugati
• 1/p + 1/q = 1/f
• conferma del principio di reversibilità del
cammino luminoso, poiché l’equazione
risulta simmetrica rispetto a p e q, per cui
se poniamo il punto oggetto in S', la sua
immagine verrà riprodotta in S.
• 1/p + 1/q = 1/f
• se pensiamo p infinitamente grande, 1/p
tenderà a zero. In tale situazione,
l’equazione assume la forma seguente:
• 1/q = 1/f ovvero q = f
• per ottenere il punto immagine nel fuoco
dello specchio occorre collocare il punto
oggetto ad una distanza infinita.
• 1/p + 1/q = 1/f
• se p = R l’equazione assume la forma
seguente:
• 1/R+1/q = 2/R ovvero q = R
• un punto oggetto coincide con la sua
immagine se viene posto in C.
• 1/p + 1/q = 1/f
• se p = R/2=f l’equazione assume la forma
seguente:
• 2/R+1/q = 2/R ovvero 1/q = 0
INGRANDIMENTO LINEARE
A
B’
B
A’
ABC e A’B’C sono triangoli simili per cui A’B’/AB=B’C/BC
B’C=R-q BC=p-R e quindi A’B’/AB = R-q/p-R ma per
l’equazione dei punti coniugati
A’B’/AB=q/p
si ottiene:
INGRANDIMENTO LINEARE
• A’B’/AB=q/p
• dall’equazione dei punti coniugati :
1/p + 1/q = 1/f segue che 1/q = 1/f - 1/p = p-f / pf
da cui q = pf / p-f sostituendo nella formula
dell’ingrandimento otteniamo:
A’B’/AB = f / p-f
quindi nota la distanza focale f, il rapporto fra
la lunghezza dell'oggetto e della sua immagine
dipende solo dalla posizione dell'oggetto nei
confronti dello specchio
SPECCHI CONVESSI
• Le regole della riflessione valgono ovviamente
anche per gli specchi convessi.
• Le regole per la costruzione delle immagini
sono le stesse anche per gli specchi convessi
• La normale alla superficie in un punto è
sempre la retta che congiunge il punto stesso
con il centro, il quale si trova stavolta dall'altra
parte della superficie speculare
• Se consideriamo un fascio di raggi paralleli all'asse
principale, i corrispondenti raggi riflessi saranno
tutti divergenti, ma in modo che i loro
prolungamenti si intersecano in un punto virtuale.
Il fuoco di uno specchio convesso è virtuale
Costruzione dell'immagine di un
oggetto esteso
• Se consideriamo un oggetto esteso, la sua immagine
si otterrà sfruttando la stessa costruzione geometrica
adoperata per gli specchi concavi. Si constata
facilmente che qualunque sia il punto dove l'oggetto
viene situato, la sua immagine sarà virtuale, diritta e
rimpicciolita
• Valgono inoltre per i punti coniugati le stesse
formule ricavate nel caso degli specchi concavi, con
la sola differenza che la distanza focale deve essere
considerata stavolta col segno negativo.
ESERCIZIO
RIFRAZIONE
• Consideriamo un raggio luminoso che viaggia
attraverso un mezzo trasparente, ad esempio
l'aria. Se sul suo cammino incontra un nuovo
mezzo trasparente, ad esempio acqua o vetro, nel
passaggio dall'uno all'altro mezzo il raggio
subisce una deviazione abbastanza netta. Si dice
in tal caso che il raggio viene rifratto.
• La riflessione della luce verifica la seguente
legge sperimentale, nota sotto il nome di Legge
di Snellius-Cartesio:
1) Il raggio incidente, la normale alla superficie
riflettente nel punto di incidenza ed il raggio
riflesso giacciono sullo stesso piano;
2)
MIRAGGIO-FATA MORGANA
• La rifrazione è anche causa di numerosi
fenomeni naturali, ad esempio il miraggio e la
fata morgana. Entrambi sono dovuti alla
diversa densità degli strati di aria, per cui
quelli più densi risultano più rifrangenti
rispetto a quelli meno densi.
MIRAGGIO
MIRAGGIO
MIRAGGIO
FATA MORGANA
DIOTTRO SFERICO
• Si definisce diottro sferico un sistema ottico
costituito da due mezzi otticamente diversi
separati da una superficie sferica
DIOTTRO SFERICO
INGRANDIMENTO
A' B': AB B' C : BC
A' B' q R
AB
pR
h h
n2 seniˆ sen sen sen
q R p
p R R p qR
h h
n1 senrˆ sen sen sen
pR q R pq R
R q
pn2 R p
q R qn1
qn1 q R
R p pn2
A' B' qn1
AB
pn2
LE LENTI
• Chiameremo lente un qualsiasi corpo
trasparente limitato da due superfici curve o da
una superficie piana e una curva, in grado di
modificare la traiettoria di un raggio luminoso
che l’attraversi.
L’oggetto è ad una distanza doppia di quella
focale
2F2
L’immagine è capovolta ma delle stesse
dimensioni dell’oggetto posta in
L’oggetto è fra
L’immagine è capovolta, ingrandita e ad una
distanza maggiore del doppio di quella focale
L’oggetto è posto nel fuoco della lente
L’immagine appare all’infinito, ingrandita e
capovolta
LENTI DIVERGENTI
• La principale differenza di una lente divergente
rispetto ad una convergente è costituita dal fatto
che un fascio di raggi paralleli all’asse principale
della lente, essi verranno rifratti in modo da
divergere e solo i prolungamenti dei raggi rifratti
concorreranno in un punto (fuoco)
Il fuoco di una lente
divergente è virtuale
• La formazione delle immagini mediante le lenti
divergenti si ottiene nello stesso modo delle
lenti convergenti
• Per quanto osservato avremo che qualunque sia
la posizione dell’oggetto rispetto alla lente, la
sua immagine è sempre virtuale, diritta e
rimpicciolita, posta dalla stessa parte
dell’oggetto
• Anche per le lenti divergenti valgono le formule
dei punti coniugati prima ricavate: si ottengono
in modo analogo purché si consideri negativa la
distanza focale f della lente.
• 1/f = potere convergente o potenza di una lente
se f è misurata in metri, 1/f viene misurata in
diottrie
OTTICA FISICA
• Quando lungo il percorso della luce vi
sono fenditure e ostacoli con dimensioni
dello stesso ordine di grandezza della
lunghezza d'onda incidente gli effetti non
sono spiegabili con l'ottica geometrica
(raggi rettilinei) ma con l'ottica ondulatoria
(di cui l'ottica geometrica è un caso
particolare).
• La luce ha anche una natura ondulatoria quindi
deve aver una lunghezza d’onda, una frequenza ed
una velocità.
• La luce si piega leggermente lungo l'orlo di barriere
aggirandole e propagandosi anche dietro di esse
quando queste hanno una dimensione dell'ordine
della lunghezza d'onda della luce.
• Questo fenomeno è detto diffrazione ed è
caratteristico di tutti i fenomeni ondulatori, ma
poiché le lunghezze d'onda della luce visibile sono
piccolissime, gli ostacoli corrispondenti dovranno
essere piccolissimi.
• Quando Francesco Maria Grimaldi (1618–1663)
notò la prima volta che i bordi delle ombre non
erano netti, attribuì questo effetto alla diffrazione
ed ebbe la netta sensazione che la luce fosse
un'onda.
INTERFERENZA
• Tomas Young (1801) dimostrò
sperimentalmente per primo la validità
della teoria ondulatoria della luce e ne
misurò la lunghezza d'onda.
• In generale si ha interferenza quando due
o più onde dello stesso tipo e stessa
frequenza, con una differenza di fase
costante tra di loro, attraversano la stessa
regione di spazio nello stesso istante.
figure interferenziali in
un ondoscopio
• Ma il risultato non fu solo questo! Quando la
luce diffratta giunse ad uno schermo si
formarono bande illuminate e bande scure
Animazione