Nome file d:\scuola\corsi\corso fisica\ottica\specchi sferici.doc
Elaborato il 18/05/2003 alle ore 12.36 ,
salvato il 17/05/03 12.33
Creato il 09/05/2003 10.33
Dimensione file: 48640 byte
stampato il 18/05/2003 12.36
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
Ottica geometrica
Specchi sferici
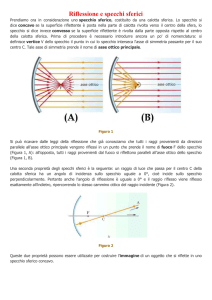
Uno specchio sferico è una porzione di superficie
sferica riflettente.
Il centro della superficie sferica è detto centro di
curvatura
Il raggio della superficie sferica è detto raggio di
curvatura
Una retta normale al piano tangente alla superficie
sferica è detta asse centrale o asse ottico, mentre il
punto in cui l’asse ottico “entra” nello specchio è
detta centro dello spechio.
Possiamo considerare riflettente sia la superficie esterna della sfera che quella interna; nel primo caso avremo
uno spechio sferico convesso, nel secondo avremo uno specchio sferico concavo.
Lo spechio sferico genera una immagine virtuale dal prolungamento dei raggio riflessi, quindi dietro la
superficie.
Lo specchio piano si può considerare come uno specchio sferico con raggio di curvatura infinito.
Costruzione immagini specchio sferico
Consideriamo un fascio di raggi paralleli all’asse ottico. I
raggio prossimi all’asse ottico vengono tutti riflessi in
prossimità di un punto detto fuoco o punto focale e la sua
distanza sull’asse ottico dal centro dello specchio è detto
distanza focale o lunghezza focale dello specchio.
Nella figura seguente si nota come il fuoco si presenti a
distanza
R
dalla superficie riflettente.
2
1/4
Nome file d:\scuola\corsi\corso fisica\ottica\specchi sferici.doc
Elaborato il 18/05/2003 alle ore 12.36 ,
Creato il 09/05/2003 10.33
salvato il 17/05/03 12.33
Dimensione file: 48640 byte
stampato il 18/05/2003 12.36
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
indicato con p la distanza dell’oggetto dalla superficie
riflettente e i la distanza dell’immagine virtuale
generata, vale la seguente equazione
1 1 1 2
+ = =
p i f R
2/4
Nome file d:\scuola\corsi\corso fisica\ottica\specchi sferici.doc
Elaborato il 18/05/2003 alle ore 12.36 ,
La relazione
salvato il 17/05/03 12.33
Creato il 09/05/2003 10.33
Dimensione file: 48640 byte
stampato il 18/05/2003 12.36
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
1 1 1 2
+ = =
si può facilmente dimostrare a partire dalla figura a fianco (n.b. nella figura è
p i f R
indicato con o la posizione dell’oggetto).
Analizzo gli angoli α , β , γ , θ e i rapporti che li legano:
β = α + θ angolo esterno al triangolo OCa
γ = α + 2θ angolo esterno al triangolo OIa
Eliminando θ avrò α + γ = 2β
Scrivo ora l’approssimazione in radianti degli angoli α , β , γ considerando i “triangoloidi” che hanno per lato
l’arco si specchio av
α≈
e sostituendo nella equazione
av
o
β≈
av
r
γ ≈
av
i
av av
av
1 1 1 2
+
=2
che semplificata darà + = =
o
i
r
p i f R
3/4
Nome file d:\scuola\corsi\corso fisica\ottica\specchi sferici.doc
Elaborato il 18/05/2003 alle ore 12.36 ,
salvato il 17/05/03 12.33
Creato il 09/05/2003 10.33
Dimensione file: 48640 byte
stampato il 18/05/2003 12.36
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
Gli specchi sferici, ancor meglio parabolici, vengono utilizzati nella costruzione di grandi telescopi per la loro
leggerezza e per l’assenza di aberrazione cromatica
4/4