“Running coupling constant”: aS(Q2)
La costante di accoppiamento aS è dipendente
dal momento trasferito nel processo: aS= aS(Q2).
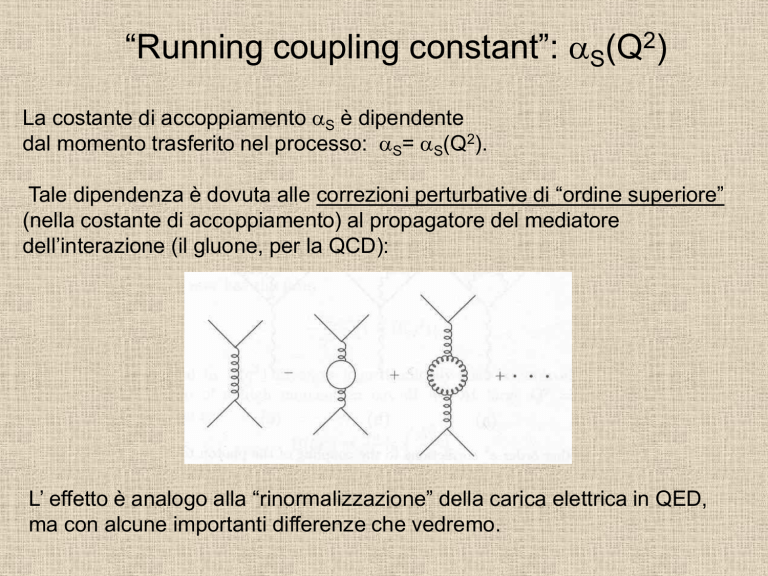
Tale dipendenza è dovuta alle correzioni perturbative di “ordine superiore”
(nella costante di accoppiamento) al propagatore del mediatore
dell’interazione (il gluone, per la QCD):
L’ effetto è analogo alla “rinormalizzazione” della carica elettrica in QED,
ma con alcune importanti differenze che vedremo.
Rinormalizzazione della carica elettrica
in QED: aQED(Q2)
In QED, l’ampiezza di scattering, ad esempio, e-e- e-e- , completa a
tutti gli ordini perturbativi è data dai diagrammi:
k
ieg
ieg
Ogni diagramma di ordine
superiore ha un contributo
più piccolo. Tuttavia la serie
non converge! Va
“rinormalizzata”
iega
q
k
~ e2a
All’ordine alpha è
p
p-q
ieg
~ e4a2
~ e6a3
g
M [eu (k ' )g u (k )] [eu ( p' )g u ( p)]
q
2
Il propagatore nell’elemento di matrice di transizione viene modificato;
limitandoci al 2o termine (in a2): ig
ig ig a
ig
q
2
q
2
2 a 2
q
q
dove il “loop fermionico” nel propagatore a è calcolabile integrando su tutti
i possibili 4-impulsi p del fermione. p è arbitrario e questo è il problema.
L’integrale è
a
a
[
e
u
(
p
)
g
u
(
p
q
)]
[
e
u
(
p
q
)
g
u( p)]
4
d p
4
(2 )
p 2 m2
( p q) 2 m 2
1
e si ottiene
p-q per un e+ uscente
equivale a q-p per un e- entrante
da p2=m2
a iga q 2(q 2 )
a
(q ) ln
3 q
con:
2
0
(a0=e2/4)
2
L’integrale diverge logaritmicamente per |p| (“divergenza ultravioletta”)
e viene controllato da un parametro di cut-off , che verrà riassorbito nella
ridefinizione (“rinormalizzazione”) della carica elettrica.
In definitiva, si ha la seguente modifica nel propagatore introdotta dal 2o
termine perturbativo:
ig
ig
2
q
2
q
2
1 (q )
e l’ampiezza di transizione è esprimibile in termini dell’ ampiezza A0(q2)
calcolata dal diagramma ‘lowest order’ (anche detto “tree-level”)
~
A1 (q 2 ) a 0 A0 (q 2 ) 1 a 0(q 2 )
dove per comodità
(q ) 1
~
si è introdotto:
(q )
ln
a
3 q
2
2
2
0
Inserendo i contributi negli ordini successivi (diagrammi a più loops), si
ottiene la serie geometrica:
a A (q )
~
~
A(q ) a A (q )1 a (q ) a (q ) ....
~
1 a (q )
2
2
2
0
0
2
0
2
2
2
0
0
0
2
0
a (q ) A (q )
2
2
0
L’ampiezza completa a tutti gli ordini perturbativi è esprimibile tramite
l’ampiezza al primo ordine in a , moltiplicata per la costante di
accoppiamento “rinormalizzata”:
a (Q )
2
a0
a 0 2
1
ln 2
3 Q
ossia:
1
1
1 2
ln 2
2
a (Q ) a 0 3 Q
A priori la ridefinizione della carica elettrica è
affetta anche dai contributi “esterni” al propagatore fotonico:
vale a tutti gli
ordini perturbativi!
Tuttavia si dimostra, come conseguenza della invarianza di gauge della
teoria, che i contributi (b) + (c) si cancellano col contributo (a) (identità di
Ward in QED; estesa alle teorie di gruppo non abeliane (e.g. la QCD) da
Slavnov-Taylor). Una ridefinizione della carica elettrica
(“rinormalizzazione”) è sufficiente alla cancellazione.
Come ha dimostrato ‘t Hooft nel 1971, l’ invarianza di gauge di una teoria
di campo è essenziale per garantirne la rinormalizzabilità, ossia la
possibilità di riassorbire le divergenze ultraviolette in un’unica ridefinizione
della costante di accoppiamento.
Negli esperimenti, ciò che si misura è a(Q2) ad una certa scala di
momento trasferito. Ad esempio, nello scattering Thomson e-e- e-eo nell’ esperimento che misura il Lamb-shift nella struttura iperfina
dell’atomo di idrogeno, a(Q2 =2 1eV2)=1/137 .
Queste misure vanno correlate con le misure a scale diverse (ad esempio
Q2 = MZ2 = (91 GeV)2 ); usando la relazione precedente,
1
1
1 2
ln 2
2
a (Q ) a 0 3 Q
si ottiene
1
1
1 2 1 2
1 Q2
ln 2
ln 2
ln 2
2
2
a (Q ) a ( ) 3 Q 3
3
La relazione tra i due valori è dunque esattamente predetta dalla teoria ed
è indipendente dalla divergenza ultravioletta (il valore di cut-off nell’integrale
dei loop fermionici interni al propagatore del fotone) che è riassorbita nella
costante di accoppiamento rinormalizzata. Invertendo la precedente si ha
a ( 2 )
a (Q )
a ( 2 ) Q 2
1
ln 2
3
2
Si noti che abbiamo introdotto
una scala arbitraria , alla quale
rinormalizziamo l’accoppiamento.
I risultati fisici non dipendono da
questa scelta!
Si noti anche che in
2
a
(
)
2
a (Q )
a ( 2 ) Q 2
1
ln 2
3
il denominatore in generale deve includere anche i fermioni più massivi
dell’elettrone, che possono circolare nei loop virtuali. In effetti la
correzione al denominatore deve contenere un fattore
Neff = nl + 3(4/9)Nu + 3(1/9)Nd
dove nl, Nu, e Nd sono i leptoni, i quarks di tipo up e down che
contribuiscono ai loops.
Simili considerazioni andranno fatte per as in QCD, come è chiaro dallo
studio del fattore R (sezione d’urto di produzione di adroni in unità di
sezione d’urto di produzione di muoni, a collisori e+e-).
I quarks però contribuiscono al running di alpha_s in modo paritario,
perché sono eguali per la QCD (che è flavor-independent).
Charge screening
La “costante” di accoppiamento è quindi una “running coupling constant”;
in QED, essa cresce logaritmicamente (ma poco!) con l’ impulso trasferito.
Qualitativamente, la cosa può essere spiegata dalla “polarizzazione del
vuoto”: le coppie virtuali e+e- che si formano agiscono come i dipoli di un
dielettrico, schermando la carica elettrica “nuda” . Quanto più ci si avvicina
ad essa, aumentando il momento trasferito nello scattering, tanto maggiore
è la carica elettrica ‘vista’ nell’ interazione.
A Q2=MZ2104 GeV2 :
ee+
e-
ea (M Z
2
1
)
132
1
1
1 Q2
1 104
ln 2 137
ln 18 132
2
2
a (Q ) a ( ) 3
3 10
a
a ( M Z2 ) a (Q 2 0)
7%
a
a
La polarizzazione del vuoto
•
Il fenomeno descritto è facilmente comprensibile e ha uno stretto analogo
classico:
se un mezzo contenente molecole dotate di un momento di dipolo elettrico
permanente è immerso in un campo elettrico, il campo viene ridotto di un
fattore e
•
L’effetto è dovuto all’orientamento dei dipoli elettrici, che operano uno
“screening” delle sorgenti del campo originario
•
A scale di distanza inferiori alle dimensioni molecolari, la carica originaria
che produce il campo si vede inalterata. Si ha che e(r)1 per r0, e(r)e
per r grandi. Questo effetto produce di fatto anche il running di aEM.
Anti-screening
• Fu scoperto da Gross, Wilczec, e Politzer nel
1973 che per teorie non abeliane come la QCD il
ragionamento visto si ribalta: i gluoni, anch’essi
portatori della carica del campo, “diluiscono” la
carica originaria, spargendola intorno ad essa.
• Il risultato è che l’interazione forte aumenta con la
distanza, mentre a piccole distanze i quarks
risultano “liberi” (asymptotic freedom). E’ questo il
motivo per cui a grande q2 i quarks appaiono
come particelle libere (permettendoci di calcolare
perturbativamente i processi di scattering).
QCD: as(Q2) e anti-screening
In QCD il meccanismo è analogo a quello visto prima, ma con l’importante
differenza che i gluoni sono portatori di carica di colore:
non esiste il
corrispettivo in QED
(vi sono due tipi di gluoni in questi loops:
trasversi e Coulomb-like; i secondi dominano
e danno il contributo di segno opposto)
Risulta che il loop gluonico contribuisce per un fattore (11/4)ln(Q2/2) e
per ognuno degli nf quarks che alla scala di Q2 considerata possono essere
creati (mf2< Q2/4) vi è un fattore –(1/6 ln(Q2/2).
In definitiva per la costante di accoppiamento forte si ha:
a S ( 2 )
a S (Q )
2
1 a S ( )
2
(33 2n f )
12
Q
ln 2
2
a S ( 2 )
Q2
1 0.61 a S ( ) ln 2
2
dove si è posto nf=5 (ci sono 5 flavours di quark: q = u,d,s,c,b ,
se si considerano le scale 2,Q2>mb225 GeV2)
La “costante” aS decresce col momento trasferito (“libertà asintotica”),
e varia molto più rapidamente di aQED.
Dallo studio dello spettro degli stati legati del charmonio (stati legati cc ):
aS(mc2 (3GeV)2) 0.278+-0.014, e propagando alla Z:
1
1
1
Q
10
0.61 ln
0.61ln
8.2
a (Q ) a ( )
10
0.278
2
2
S
2
4
2
S
[ in realtà si dovrebbe calcolare una doppia propagazione: a(mc2)a(mb2) con b0(nf=4)=0.66,
e a(mb2) a(mZ2) con b0=0.61; la differenza è piccola ]
a S (M Z 2 ) 0.12
a s
as
a s ( M Z2 ) a s (10GeV 2 )
50%
as
Tale predizione è verificata molto bene
sperimentalmente, dalle misure di aS(MZ2)
ottenute, ad esempio, dalla forma degli
eventi di decadimento adronico della Z:
Z qq ; tale forma dipende dal numero
di gluoni irradiati dai quarks nello stato finale,
che dipende da aS.
Decadimenti di quarkonio e as
• Gli stati legati q-antiq come il charmonio (Y) o il bottomonio (U)
permettono di calcolare as a q2 ben definito (=m2)
• Prendiamo la Y: è uno stato 1-- e non può decadere in uno o due
gluoni per color conservation e C-parity, rispettivamente
• Si studia il rapporto fra le larghezze di decadimento in due muoni o
in adroni, G()/G(ggg), che non dipende dalla forma specifica della
funzione d’onda dei due quarks. Calcoli teorici prevedono per
questo rapporto il valore
G
9
a a ( ) 33 2 N
1
3
ln
0
.
43
...
G
10( 9) a ( )
12
m
2
s
2
ggg
3
s
f
2
Q
Esercizio 1: verificare che da R(1S)=0.032±0.001,
R(2S)=0.031±0.008, R(3S)=0.032±0.003 si trova rispettivamente
as=0.1743±0.0024, 0.175±0.015, 0.1742±0.0021.
as(Q2) e QCD
La dipendenza di aS(Q2) a S (Q )
a S ( 2 )
2
1 a S ( )
2
(33 2n f )
12
Q
ln 2
2
a S ( 2 )
Q2
1 0.61 a S ( ) ln 2
2
può essere riformulata introducendo il parametro dimensionale QCD :
1
1
1
Q
Q
b ln b
ln
a (Q ) a ( )
b a ( )
2
2
2
S
0
2
S
b ln
0
2
2
QCD
dove:
0
2
0
Q
ln
2
ln 2
QCD
2
2
1
b a ( 2 )
0 S
Con tale definizione, si trova
S
2
2
(b0 (33 2n f ) / 12 )
ovvero
ln 2QCD ln 2
Q2
1
b0 ln 2
2
a S (Q )
QCD
e in definitiva
1
b0a S ( 2 )
Q 2
2
a S (Q ) b0 ln 2
QCD
relazione che permette di calcolare aS senza alcun riferimento ad una
scala prefissata 2 (ovviamente QCD viene determinata dalla misura di
as(2) ad una certa scala; il ‘best fit’ ai dati dà QCD= (20515) MeV).
1
Come detto in precedenza nel discutere le scaling violations,
la produzione di jets nel DIS è sensibile al valore di aS
Evento dijet in H1
aS(Q2)
Così pure la sezione d’urto differenziale
ds/dETjet :
buon accordo con le misure
di LEP negli eventi Z qq
aS(Q2) e jet production in e+eLa molteplicità dei jets è stata misurata anche ai collisori e+e-:
e+
g
Z/g
q
aS
e-
Evento e+e- Z q q + gluone
al LEP ( s 91.2GeV ; esperimento DELPHI)
q
La definizione di “jets”
(e quindi di eventi a 2-3-4..jets)
dipende dall’ algoritmo e dai
parametri che regolano la
‘clusterizzazione’ delle particelle
(gli oggetti misurati sono gli
adroni che emergono dal processo
di frammentazione del quark o
del gluone originario)
Frammentazione dei jets
Il processo di produzione degli adroni, con la frammentazione dei
jets primari (i quarks e i gluoni), comprende varie fasi:
Processo elettro Processo
-debole (QEWD), di QCD,
trattabile
perfettamente
a livello
calcolabile
perturbativo
informazione
su as
decadimenti
deboli degli adroni
instabili
“adronizzazione”
(formazione degli adroni
in regime non perturbativo), descritto da
modelli fenomenologici (es.”parton
shower”); non modifica sostanzialmente
le distribuzioni dei jets primari
aS(Q2) e multi-jets
Esempio: algoritmo di ricombinazione basato
sulla variabile:
2
y
M ij
2
Evis
energia totale visibile
nell’evento
pi ( Ei , pi )
qij
p j (E j , p j )
M ij2 2Ei E j (1 cosqij )
Le particelle vengoni ricombinate, attuando la sostituzione (pi,pj)pk=pi+pj
ricursivamente, finché tutte le “pseudo-particelle” hanno ykm > ycut
Le pseudoparticelle rimanenti
sono i “jets” dell’ evento;
Le frequenze
R(n-jets) = N(n-jets)/Ntot eventi
sono funzione di ycut
parametro
fissato
a priori
aS(Q2) e multi-jets
Ai diversi collisori e+e- (PEP, PETRA, TRISTAN, LEP) che hanno operato a
diverse energie, la frequenza di eventi a 3-jets per un fissato valore del
parametro di ricombinazione varia con l’energia nel CM della collisione
Ciò è diretta
conseguenza della
dipendenza dal q2
di aS(q2)
In collisioni adroniche si usano, invece del KT, algoritmi “a cono” che cercano di
massimizzare l’energia entro cerchi di raggio fisso nello spazio hf
Ci sono diversi problemi, sia di carattere teorico che sperimentale, nella connessione
fra jet ricostruiti con questi algoritmi e i partoni prima dell’adronizzazione:
– Teorici: divergenze collineari e soft (“infrared safety”), separation, counting
– Sperimentali: soft-gluon emissions (out-of-cone), instabilità della ricostruzione, contributi di
background da multiple-parton scattering e pileup...
L’argomento è complicato ma molto interessante... forse troveremo il tempo di
discuterne più in dettaglio più avanti.
Evento multi-jet
di CDF e
diversa
ricostruzione
con due algoritmi
a cono diversi
E a LHC...
Candidato top-antitop di CMS
Dijet event di altissima energia
A LHC sono in uso sia algoritmi a cono
che KT-based. Lo vedremo più avanti.
Maggiore è l’energia dei jets, e più
facile è la loro ricostruzione univoca,
perché la dimensione trasversa dei jets
scala con l’inverso del logaritmo del q2:
<q>=k/[(log(q2)]
Questo è dovuto alla decrescita di as
Sommario di
misure di as
Vi sono svariati modi per
determinare sperimentalmente
la costante della QCD. Si
sfruttano osservabili di DIS,
decadimenti adronici del tau,
forme dei jets, osservabili nel
decadimento adronico della Z,
sezioni d’urto di 3/2 jets...
Si può anche calcolare as con
calcoli sul reticolo, e i risultati
sono in accordo con
l’esperimento.
Tutti i metodi danno valori
consistenti, una volta “evoluta”
as a un valore comune di Q2.
Una nota sulla fattorizzazione
• Le sezioni d’urto di processi con adroni nello stato iniziale dipendono,
ovviamente, dalle parton distribution functions
• Si è visto che le PDF dipendono da x e q2
• In QCD è ben verificata l’ipotesi di “fattorizzazione” della sezione d’urto:
questa si può cioè ricavare da un integrale in cui compaiono le PDF come
fattori, e una “sezione d’urto puntuale”. Le PDF sono generali, e non
specifiche di un processo. Si possono “fattorizzare” nel calcolo:
s ( P , P ) dx dx Q ( x , )Q ( x , )sˆ [ x P , x P ,a (q)]
1
2
ij
1
2
i
1
F
j
2
F
1
1
2
2
s
Le previsioni teoriche per la sezione d’urto dei processi ai collider
adronici sono quindi dipendenti dalla scelta di una scala di fattorizzazione
F.
Una misura di as a CDF
•
Vediamo un po’ in dettaglio una misura di alpha_s ottenuta in collisioni
adroniche al Tevatron collider.
•
Una misura di as può essere ottenuta in collisioni adroniche dallo spettro
differenziale di produzione di jet in funzione dell’energia trasversa.
•
La misura si ottiene dal confronto dello spettro dN/dET osservato con le
previsioni della QCD, che viene calcolata al next-to-leading order nello
sviluppo di as. Data la grande energia dei processi studiati, i calcoli perturbativi
funzionano bene (as è piccola al q2 in questione).
•
Si usa l’espressione
ds/dET = as2(R) X(F,ET) [1+as(R)k(R,F)]
ove R e F sono legati al valore di ET indagato, e k è un fattore di correzione
calcolabile con simulazioni Monte Carlo, che connettono l’elemento di matrice
con le quantità osservabili qui entra in gioco un parametro fenomenologico
che descrive quando due partoni sono osservati come jets separati o meno.
La distribuzione di dN/dET si tramuta subito in una misura di as, che
si vede dipendere dalla scala del processo attraverso la quantità
misurata, ET. Con l’equazione di evoluzione si riporta poi la misura
al q2 di LEP, preso ormai da tutti come riferimento (punti rossi).
Nel calcolo entrano ovviamente in
gioco le PDF dei quarks e gluoni
nei proiettili (protoni e antiprotoni):
si usa “fattorizzare” nel calcolo
della sezione d’urto la probabilità
di osservare partoni di un certo
valore x, e la sezione d’urto
“puntuale” del processo di hard
scattering.
Ciò porta con sé una definizione
di una “scala di fattorizzazione” F
e relative sistematiche...
La misura di as in collisioni
adroniche è resa imprecisa dalle
ineludibili sistematiche, però ci
permette di vedere in un solo
dataset il “running”...
Il risultato è una misura di as che ha errori teorici confrontabili con
quelli sperimentali, e pari all’incirca al 5-6%:
•Gli errori teorici vengono
soprattutto dalla scelta delle
scale F e R, e dalle PDF
(che a loro volta sono
determinate assumendo un
certo valore di as... la
circolarità è evitata con studi
dettagliati).
Risulta chiaro che i colliders
adronici hanno difficoltà a
misurare la costante di
QCD, per via del doppio
ruolo che essa ricopre in
questi processi, nello stato
iniziale e finale.
La più recente misura di D0
• D0, l’esperimento concorrente a CDF al Tevatron, ha misurato as
con dati del Run II – vedi arxiv:1006.2855
• 8 anni dopo la misura di CDF, le sistematiche teoriche sono minori:
esistono calcoli che includono i diagrammi più importanti al NNLO, le
PDF sono più precise.
La maggior quantità di dati e la miglior
comprensione del rivelatore che ne
deriva hanno anche diminuito le
sistematiche sperimentali
D0 utilizza solo eventi con jets centrali,
dove il detector è meglio calibrato, e
a energia non troppo alta per evitare
una regione dei dati ove la sezione
d’urto di jet production è stata usata
nel calcolo delle PDF!
• I risultati, una volta estratta as dalla sezione d’urto e
evoluta alla scala comune MZ, sono molto precisi e
competitivi con quelli di altri esperimenti
• Nel grafico sono mostrati i punti sperimentali di D0
confrontati con le determinazioni di as a HERA
La misura finale ha un’incertezza totale
del 4%, che è un ottimo risultato per
un collider adronico
Notare che le barre di errore
dei punti neri sono la somma di
tutte le incertezze – e sono quindi
altamente correlate fra loro!
Il Settore di Higgs
del Modello Standard
PARTE I: La Lagrangiana del Modello Standard
–
–
–
–
–
–
Introduzione alle simmetrie di gauge
Simmetrie esatte, rotte, nascoste
Il teorema di Goldstone
Rottura della simmetria di gauge e meccanismo di Higgs
Lagrangiana del Modello Standard
Accoppiamenti, masse e implicazioni
PARTE II: Fenomenologia del bosone di Higgs e ricerche sperimentali
–
–
–
–
–
–
–
Considerazioni teoriche
Correzioni radiative e constraints da fit elettrodeboli
Decadimenti
Meccanismi di produzione in collisioni elettrone-positrone
Meccanismi di produzione ai colliders adronici
Ricerche dirette a LEP II e limiti sperimentali
Ricerche del bosone di Higgs al Tevatron
• Apparati sperimentali: CDF e D0
• Sezioni d’urto, stati finali accessibili
• Tecniche sperimentali
• Qualche esempio in dettaglio
– Prospettive della ricerca a LHC
• Produzione a LHC e stati finali promettenti
• Tecniche di ricerca
• Alcune misure in corso
• Prospettive per il 2011
Introduzione:
Simmetrie di gauge e MS
A bassa energia le interazioni forte, em e debole sembrano indipendenti: hanno
sezioni d’urto che differiscono di 12 ordini di grandezza diverse costanti di
accoppiamento
La speranza di descrivere queste interazioni con un unico campo unificato, ad
alta energia, ricevette verso la fine degli anni ’60 una spinta dalla formulazione
GSW (Glashow, Salam, Weinberg) dell’unificazione elettrodebole.
Il passo teorico più importante in questa direzione è realizzare che le interazioni
fondamentali sono invarianti per trasformazioni locali di gauge
Per formulare una teoria di gauge bisogna scrivere una Lagrangiana che
descriva la cinematica e le interazioni fra i campi, e sia invariante sotto
trasformazioni di simmetria che permettano la conservazione delle quantità
rilevanti: carica elettrica, colore, isospin e ipercarica deboli. Queste quantità
sono conservate localmente, per non entrare in conflitto con la relatività speciale.
La formulazione Lagrangiana ha il vantaggio che dallo studio delle proprietà
invarianti di L si arriva naturalmente alle quantità conservate della teoria. La
connessione per trasformazioni continue è data dal teorema di Noether.
Reminder: formalismo Lagrangiano
•
Classicamente L=T-V permette, attraverso le equazioni di Eulero-Lagrange,
di derivare le equazioni del moto.
d L L
0
dx q q
i
•
x
i
L
(f / x
L
0
) f
Facciamo alcuni esempi di densità Lagrangiane che useremo nella
costruzione della teoria elettrodebole:
1
1
L ( f )( f ) m f
2
2
f mf 0
2
KG
2
: Klein-Gordon
L i g m
2
Dirac:
1
L F F j A
4
F j
M
D
ig m 0
: Maxwell
Dalla densità Lagrangiana estraiamo “regole di Feynman” che ci permettono di
scrivere i propagatori (dai termini quadratici nei campi e derivate) e i fattori di vertice
della teoria (dagli altri termini). Con questi calcoliamo le ampiezze dei processi da
espansioni perturbative attorno allo stato di minima energia.
Invarianza di gauge globale
L (ig m)
La Lagrangiana di elettrone libero
è invariante per trasformazioni U(1) globali
e questo implica che
' e
iq
0 L 2q ( g )
per arbitrari valori della fase globale .
Esercizio n.2: dimostrare l’affermazione qui sopra, usando le equazioni
di Eulero - Lagrange
Ciò implica la conservazione di una densità di quadricorrente
j (q g ) 0
e quindi della carica elettrica q, integrando nelle coordinate spaziali e
usando il teorema della divergenza:
q j d x
0
3
dq
a j a d 3 x j ds 0
dt
a 1, 3V
S
Invarianza di gauge locale e QED
La Lagrangiana di elettrone libero
L (ig m)
rimane invariante per trasformazioni U(1) locali
' eiq ( x )
solo se si introduce una corrispondente variazione nella legge di trasformazione
delle derivate del campo fermionico, una derivata covariante
definita da D iqA (x) e che trasforma come
e in cui il campo vettoriale A trasforma come segue:
D eiq ( x ) D
A ( x) A ( x) ( x)
La Lagrangiana che deriva dall’inserimento della derivata covariante D contiene
ora un termine di accoppiamento della corrente vettoriale e il campo A:
L i g m qA g
e un termine cinetico 1 ( A A )( A A )
4
Il termine cinetico del campo A è invariante per la trasformazione vista, ma un
termine m2AA non è permesso perché non trasforma in se stesso: l’invarianza
locale di gauge richiede che la carica conservata sia sorgente di un campo
vettoriale privo di massa.
Ricordiamo quindi che:
• Invarianza globale di gauge conservazione carica elettrica
• L’imposizione di invarianza locale di gauge per la Lagrangiana di un
campo di Dirac forza l’introduzione di una derivata covariante, e un
campo di gauge A associato al fotone. Si ottiene la Lagrangiana di
QED
• Invarianza locale di gauge introduzione di un campo vettoriale a
massa nulla (consistente con il range infinito dell’interazione). Un
termine di massa per il fotone romperebbe l’invarianza di gauge per
via delle proprietà di trasformazione del campo A.
• Questo vale per qualunque bosone vettore. I bosoni deboli non
sfuggono alla logica. Se vogliamo invarianza locale di gauge, i
bosoni rimangono a massa nulla.
•
•
In contrasto con la richiesta formale di bosoni mass-less nella teoria,
l’esistenza di correnti deboli cariche mediate da bosoni vettori massivi è
necessaria per evitare divergenze nelle sezioni d’urto di scattering.
Esempio: e-e scattering s prop. a G2s,
mentre l’unitarietà dello sviluppo in onde
parziali della sezione d’urto (J=1) implica
W
che s sia minore di 1/s per
e
e
e
2
s>1/G = 90000 GeV
la sezione d’urto viola l’unitarietà.
g2 / M 2
G / 2
F
e
W
Invece, se il propagatore del W contiene un termine di massa, esso rende
finita la sezione d’urto.
•
Violazione dell’unitarietà nei diagrammi all’ordine più basso e non
rinormalizzabilità dei diagrammi ad ordini superiori sono strettamente legate:
l’una implica l’altra.
•
In ogni caso, due bosoni W+ e W- non bastano a rendere la teoria
consistente: la sezione d’urto del processo di produzione di coppie W W
rimane divergente, sia per interazione debole W W che e.m. eeW W.
Si può osservare, dalla struttura della teoria, che la divergenza del processo
W W si può neutralizzare con diagrammi mediati da un bosone neutro
massivo Z. Lo Z permette anche di neutralizzare la divergenza del processo
elettromagnetico, mediante diagrammi che singolarmente sono divergenti.
– NB: La predizione di processi con correnti deboli neutre (come lo scattering -e),
che se mediati da scambio di un solo bosone vettore dovevano avere sezioni d’urto
comparabili a quelli con scambio di corrente carica (come e-e), fu uno dei grandi
successi della teoria elettrodebole.
Gargamelle vede pochi eventi di interazione di antineutrino-elettrone, su 730,000
fotografie. Sono le prime evidenze sperimentali che il modello GSW è corretto, dopo 6
anni dalla sua pubblicazione...
• La cancellazione fra diagrammi con bosoni W e Z è possibile solo se
gli accoppiamenti ai leptoni dei bosoni W, Z, g sono di intensità
confrontabile: g ~ e.
• Questa unificazione elettrodebole necessita che W e Z abbiano
masse dell’ordine dei 100 GeV. Ciò apparentemente è in conflitto
con l’invarianza locale di gauge della Lagrangiana.
Vedremo che l’introduzione di
un campo scalare h e un
meccanismo appropriato
risolvono il problema. In più, h
permette la convergenza dello
scattering W WW W, che
rimaneva divergente (anche se
in maniera meno severa degli
altri processi discussi sopra).
Ma perché insistere con la gauge locale?
Sia i fotoni che i gluoni hanno massa nulla, e questo si sposa bene con la struttura delle
rispettive Lagrangiane con invarianza di gauge.
Per le interazioni deboli, che richiedono bosoni vettori di massa O(100 GeV), questo è invece
un problema. Ma perché non dimenticarsi dell’invarianza locale e aggiungere a L termini di
massa?
Se si fa questo, si finisce in una teoria senza senso, perché ogni quantità calcolabile da essa
conterrà divergenze non rinormalizzabili.
Esempio: nello scattering fra due elettroni
si hanno diagrammi come quello a fianco.
e
Essi contribuiscono all’ampiezza con
q
Z
Z
integrali del tipo
d 4 q ( propagatori )
e
Mentre in QED la forma 1/q2 del propagatore dei due fotoni scambiati rende finito l’integrale,
per bosoni massivi il risultato diverge, data la costanza del propagatore a q2 grande:
i
g q q / M 2
q M
2
2
q
2
iq q
q2M 2
Se poi si regolarizza l’integrale introducendo un cut-off, si scopre che altri diagrammi con più
loops richiedono altrettanti cut-offs indipendenti. Serve quindi un numero infinito di parametri
arbitrari, e la teoria non ha più senso: essa è non rinormalizzabile.
Rottura spontanea di una simmetria discreta
Consideriamo la Lagrangiana
L T V
1
1
1
( f ) 2 ( 2f 2 lf 4 )
2
2
4
Con l>0, essa possiede una simmetria discreta rispetto all’operazione di
riflessione f -f.
Se prendiamo 2>0, L descrive particelle a spin 0 e massa ; il termine
quartico nel campo dètta l’autointerazione del campo con vertici a 4
particelle, con un auto-accoppiamento di intensità l.
Invece, se prendiamo 2<0, non sappiamo come interpretare il
termine f2, perché la massa della particella sarebbe immaginaria.
La forma del potenziale nei due casi
è mostrata a lato. Mentre per 2>0 lo
stato f=0 è un minimo, nel caso 2<0
il minimo del potenziale si ha per
f v 2 / l
Poiché in fisica delle particelle non siamo in grado di calcolare le
quantità fisiche esattamente, ma dobbiamo ricorrere a espansioni
perturbative (per calcolare le ampiezze con le regole di Feynman)
attorno a un minimo del potenziale, è opportuno operare una
traslazione del campo attorno al minimo:
f ( x) v h ( x)
Si ottiene allora una nuova forma per L (che descrive la stessa fisica!):
L'
1
1
( h ) 2 l v 2 h 2 l vh 3 lh 4
2
4
Questa Lagrangiana ha un termine di massa del segno corretto per la
fluttuazione h(x), mentre i termini di ordine superiore in h
rappresentano le autointerazioni del campo.
La massa del campo scalare è ricavabile dal termine quadratico:
mh 2l v2 2 2
Abbiamo quindi scoperto che nel caso 2<0 L e L’ rappresentano in
effetti un campo scalare massivo. In teoria delle perturbazioni L’
fornisce risultati sensati, mentre L no, perché espansioni perturbative
attorno a f=0 non convergerebbero
Alcune considerazioni sulla “rottura” di simmetria
• La traslazione operata nel campo, che trasforma L in L’, rende nascosta
la simmetria: intorno al punto di minima energia L’ non è più invariante
per trasformazioni f-f.
• E’ la presenza di una degenerazione nello stato di vuoto che rende
arbitraria la scelta di esso, e di conseguenza nasconde la simmetria
originale di L.
• Tuttavia per valori grandi dell’energia (rispetto alla massa del campo), la
teoria ritorna ad avere la sua simmetria per riflessione: in quel caso, la
massa della fluttuazione quantistica h(x) non è più rilevante per
determinare la fisica, e la simmetria ritorna ad essere apparente.
• Vi sono in natura diversi sistemi che manifestano lo stesso meccanismo.
Sono tutti esempi della stessa situazione: casi in cui è energeticamente
favorevole per lo stato fondamentale avere un valore non nullo di un
campo.
– Ferromagneti infinitamente estesi: ground state non simmetrico, L
simmetrica
– Flessione di un chiodo di plastica: L simmetrica, flessione no
– reticoli cristallini
Una nota sull’energia del vuoto
Consideriamo V(f) = ½ 2f2 + ¼ lf4 : i due minimi degeneri si trovano a V<0.
Con l’aggiunta di una costante (che non cambia l’equazione dei campi!) si può
riscrivere V in modo che il vuoto si trovi a V’=0:
V’(f) = ¼ 4/l ½ 2f2 ¼ lf4 ¼ lf22/l2.
Notare che per le equazioni del moto conta la derivata del potenziale...
Dai dati sull’espansione dell’universo, l’energia del vuoto è
sì negativa, ma estremamente piccola rispetto al valore
indicato da V, che per l=1, =1 GeV vale 1041 GeV/cm3
(da confrontare con 10-6 GeV/cm3 che è la densità di
energia media dell’universo).
•
In fisica delle particelle possiamo benissimo decidere
di considerare V’ invece di V.
In generale vi sono diversi contributi all’energia del vuoto
da fluttuazioni virtuali di ciascun campo, dalla loro energia
potenziale, e anche una costante cosmologica. Tutti questi
contributi sono enormemente più grandi in valore assoluto
del valore misurato. Che si combinino per dare un numero
così vicino a zero è quantomeno sospetto. Questo è detto
“cosmological constant problem”.
Note addizionali sul valore del potenziale
nello stato di minima energia
•
Se non fosse per la gravità, il potenziale potrebbe essere traslato senza
problemi.
•
Tuttavia, uno dei postulati della relatività generale è che la gravità
interagisca con ogni forma di energia e momento, e quindi anche con
l’energia del vuoto. Ciò distingue il valore assoluto del potenziale!
•
Solo per la gravità questo è vero. Quindi ogni manifestazione sperimentale
di una costante cosmologica è attraverso la sua interazione gravitazionale.
•
Se calcoliamo ad esempio l’effetto di una densità di energia del vuoto di
1092 g/cm3, troviamo che la radiazione di fondo si sarebbe raffreddata sotto
3K nei primi 10-41 secondi dopo il Big Bang.
•
La piccolezza dell’energia del vuoto è un problema aperto in cosmologia.
Simmetrie esatte, nascoste, e rotte
A seconda della dinamica della teoria, le simmetrie della funzione L possono
manifestarsi in molti modi diversi.
– Una simmetria di L rimane una simmetia della fisica che ne ha origine. Esempi sono
SU(3) di colore o U(1) elettromagnetica
– La simmetria di L è solo apparente, perché in realtà essa ha un’anomalia. U(1) assiale è
un esempio nello SM. Un’anomalia avviene quando una simmetria delll’azione non è una
vera simmetria della teoria quantistica corrispondente. Non ce ne occupiamo in questo
corso (a parte un accenno nell’introduzione al top quark).
– La simmetria di L può essere rotta esplicitamente da termini non invarianti. Un esempio è
la simmetria di Isospin SU(2) tra u e d, che è rotta dall’elettromagnetismo e dalla
differenza di massa dei due quarks. E’ una simmetria approssimativa.
– La simmetria di L può infine essere nascosta, ovvero l’operazione può lasciare L
invariante ma modificare lo stato fondamentale. In questo caso non è apparente la
simmetria nello spettro degli stati fisici. Ci sono due modi in cui questo può accadere:
• Uno o più campi scalari acquistano valori diversi da zero nel vuoto: si tratta di rottura spontanea
di simmetria, il cui esempio più lampante è SU(2)L rotta dal campo di Higgs nelle interazioni
deboli
• Quando sono effetti quantistici non presenti nella Lagrangiana classica a rompere
dinamicamente la simmetria, non si osservano corrispondenti campi scalari. Un esempio è la
rottura della simmetria chirale di QCD, SU(2)LxSU(2)R.
Il teorema di Goldstone
Consideriamo ora un campo scalare complesso
e dunque la forma
f
1
(f1 if2 )
2
L ( f )* ( f ) 2f *f l (f *f )2
L è in questo caso invariante per una trasformazione di fase globale
feiaf : possiede una simmetria per trasformazioni U(1) e la fisica non
dipende da a.
Prendiamo l>0, 2<0 ed esplicitiamo la dipendenza di L dalle componenti
reale e immaginaria di f:
L
1
1
1
1
2
2
2
2
( f1 ) 2 ( f2 ) 2 2 (f1 f2 ) l f1 f2 2
2
2
2
4
Si vede che in questa formulazione il potenziale V(f) ha un minimo per
tutti i valori del campo tali che f12+f22 = v2 = -2/l .
Questa volta abbiamo un’infinità continua di minimi per V, organizzati in
una circonferenza di raggio v attorno a f=0. Come nel caso scalare reale,
ci troviamo nella necessità di scegliere un valore del minimo attorno al
quale operare i calcoli perturbativi per estrarre la dinamica di f da L.
f2
Scegliamo espansioni intorno al vuoto f1=v, f2=0 scrivendo
(v,0)
f(x) = [v+h (x)+ix (x)]/2½
f1
e sostituiamo l’espressione in L. Otteniamo una nuova forma L’:
L'
1
1
( x ) 2 ( h ) 2 2h 2 c (h 3 ) (hx 2 ) (h 4 ) (x 4 ) (h 2x 2 )
2
2
ove si sono espressi in forma concisa i coefficienti nei termini di
autointerazione dei campi.
Espressa con x e h L’ possiede due termini cinetici ma un termine di massa
solo per h:
2
mh 2
Il campo x tangenziale alla circonferenza di minimo potenziale non incorre in
resistenza dal potenziale per piccole oscillazioni intorno al minimo (v,0), e
rimane a massa nulla. E’ la presenza di una degenerazione dello stato di
vuoto a mantenere nulla la sua massa.
La rottura della simmetria di L ha apparentemente avuto un effetto nefasto,
in quanto oltre al campo massivo h che volevamo generare, compare uno
scalare massless, x. x è detto bosone di Goldstone.
Il caso considerato è solo un caso particolare di un teorema generale, il
teorema di Goldstone: la rottura spontanea di una simmetria continua
genera bosoni scalari a massa nulla.
Esercizio n°3: dimostrare che la Lagrangiana per tre campi
scalari interagenti
1
m2
L f i fi
fifi l (fifi ) 2
2
2
descrive un campo scalare massivo e due campi scalari a massa
nulla.
(Hint: trovare l’espressione del minimo del potenziale, e
scegliere opportunamente il valore del campo nei
dintorni del vuoto.)
Quanto visto sembra implicare che la strada che stiamo percorrendo per
dotare la nostra teoria elettrodebole di bosoni massivi è destinata a fallire, in
quanto oltre ai bosoni massivi si generano campi scalari a massa nulla che
non si osservano in natura: non esistono particelle scalari a m=0!
Tuttavia, vedremo che succede qualcosa di diverso quando si applica il
meccanismo di Goldstone alla Lagrangiana SU(2)xU(1) del modello
elettrodebole.
Il meccanismo di Higgs
Il modello di Goldstone ora visto si può dotare dell’interazione
elettromagnetica tenendo presente il principio di gauge e passando a una
simmetria U(1) locale:
1
L ( iqA )f * ( iqA )f 2f f l (f f ) 2 F F
4
F A A
f1 v h ( x)
Prendendo lo stato di vuoto in (v,0) e scegliendo l’espansione
f2 x ( x )
la Lagrangiana diventa
1
1
1
1
L ( h )( h ) lv 2h 2 ( x )( x ) q 2 v 2 A A qvA x Fv F v ...
4
2
2
2
C’è una difficoltà rispetto a prima: il campo scalare h ha ora massa (2lv2)1/2 ,
x è rimasto a massa nulla, e il campo di gauge A ha massa qv: questo
corrisponde a un grado di libertà in più rispetto alla Lagrangiana di partenza!
In più, il termine che mescola A e la derivata di x ci suggerisce che non
stiamo guardando gradi di libertà ortogonali fra loro (in teoria dei campi
questo termine permette la transizione A x durante la sua propagazione).
Il grado di libertà in più è fittizio: una scelta dello stato di vuoto non introduce
nuovi gradi di libertà! Il campo x è in effetti irrilevante per la fisica, e
possiamo scegliere un particolare forma per la trasformazione di gauge che
lo elimini.
Scriviamo allora il campo nella forma modulo*exp(fase), invece che nella
forma solita v+h+ix:
1
[ iq ( x ) / v ]
f ( x)
2
[v H ( x)]e
Se ora applichiamo al campo una gauge locale U(1) abbiamo
f ' ( x) exp(iq( x))f ( x)
il che significa che dobbiamo avere
[v H ' ( x)] exp(iq ' ( x) / v) exp(iq( x))[v H ( x)] exp(iq ( x) / v)
Da ciò segue che poiché c’è invarianza di gauge, le fluttuazioni H’ e q’
trasformano come: H ' ( x) H ( x)
q ' ( x) q ( x) qv ( x)
E’ quindi chiaro che scegliendo la fase
1
( x) q ( x)
qv
NB: nel caso del campo scalare complesso
con L invariante per U(1) globale eia, nessuna
scelta della fase costante a può cancellare
Il campo x(x), qui invece la simmetria per
fasi (x) dipendenti da x ce lo permette!
(chiamata gauge unitaria) abbiamo q’(x)=0. I bosoni di Goldstone
corrispondono ai quanti del campo q(x): attraverso la scelta della gauge, li
abbiamo eliminati dallo spettro della teoria!
E’ chiaro che i bosoni di Goldstone sono “oscillazioni” nel parametro
che distingue diversi stati di vuoto: la fase q(x). Scegliendo la gauge
unitaria abbiamo rimosso il grado di libertà non voluto.
Usando le regole di trasformazione del campo scalare e del campo di
gauge per U(1) locale, con la scelta della fase vista sopra:
1
A ' ( x) A ( x ) q ( x)
L ora contiene due campi
qv
interagenti: uno scalare
massivo H, e un vettore
massivo A. Siamo sulla
buona strada...
1
[v H ( x )]
2
possiamo allora riscrivere la Lagrangiana:
1
1
1
L [ ( H ) 2 lv 2 H 2 ] q 2 v 2 A A q 2 A A H 2
2
2
2
4 gradi di libertà
1
1
1 4
2
3
4
v
q vA A H lvH lH Fv F lv
il termine misto
4
4
4
è scomparso
Come promesso, L non contiene traccia della fase q(x).
f ' ( x)
La trasformazione di L in una forma che esplicita il trasferimento di
gradi di libertà associati a bosoni di Goldstone a componenti
longitudinali di bosoni vettori è noto come meccanismo di Higgs.
Quello visto sopra è il caso U(1).
Trasformazioni SU(2) e Yang-Mills
Per introdurre il modello standard conviene prendere in considerazione due campi di Dirac
che trasformino come un doppietto per una simmetria interna SU(2) di isospin.
1
( )
2
L (ig m)
Richiediamo che la Lagrangiana sia invariante per trasformazioni SU(2) locali infinitesime:
' e [1 i / 2]
i / 2
i j
I generatori di SU(2) non commutano (il gruppo non è abeliano):
[
,
2 2
] ie ijk
k
2
In analogia con la QED possiamo richiedere la gauge invarianza locale usando derivate
covarianti:
D ig
j
2
Wj
1
W W W
g
I campi W devono trasformare come segue:
Il termine cinetico dei campi contiene ora un’autointerazione dei W, in quanto
W W W gW W
La Lagrangiana è invariante per SU(2) locali ma non ammette un termine di massa per i
W. Le teorie di Yang-Mills richiedono l’esistenza di campi vettoriali a massa nulla. A noi
serve una teoria di YM, ma dobbiamo generare una massa per i bosoni vettori deboli...
Il meccanismo di Higgs in SU(2)
Prendiamo allora in considerazione la rottura spontanea della simmetria locale di
gauge del gruppo SU(2)L. Questo gruppo non è scelto a caso, ma è il punto di arrivo
dell’indagine di Glashow, Salam e Weinberg per inserire in una teoria di gauge i
bosoni vettori massivi W. Il fotone arriverà includendo U(1)...
Si parte da una Lagrangiana che descrive un doppietto di campi scalari: 4 gradi di
libertà. Ci servono 3 di questi per dotare i bosoni vettori della teoria GSW di massa…
L ( f )† ( f ) 2f †f l (f †f )2
fa
1 f1 if2
f ( )
(
)
fb
2 f3 if4
Scriviamo i campi come segue:
Sotto una trasformazione SU(2) globale dei campi f,
f f' e
(
i j j
2
)
f
L è chiaramente invariante. Per renderla localmente invariante introduciamo un
parametro di gauge (x) e rimpiazziamo la derivata con una covariante:
f ( x) f ' ( x) [1 ( x) / 2]f ( x)
Wj è un tripletto di campi di gauge
e per rotazioni infinitesime di SU(2)
trasforma come segue:
D ig
j
2
Wj
1
W W W
g
Con l’introduzione della derivata covariante, la Lagrangiana gaugeinvariante diventa
1
L ( f ig Wf ) ( f ig W f ) V (f ) WW
2
2
4
†
L’ultimo termine rappresenta l’energia cinetica dei campi di gauge,
prodotto dei tre tensori W: W W W gW W
Siamo interessati a condizioni di vuoto degeneri, per cui se ora poniamo
come al solito l>0, 2<0, il potenziale
2
†
†
2
V (f ) f f l (f f )
ha un minimo in
2
f
1
v
f †f (fa *fb* )( a ) fa *fa fb*fb (f12 f2 2 f3 2 f4 2 )
fb
2
2
Scegliamo ora f3
“nascondendo” la simmetria SU(2)
nello stato di vuoto. Possiamo allora espandere il campo
nell’intorno del vuoto scelto, scegliendo una fase tale che
2=v2,
0
1
f ( x)
2 v H ( x)
(
)
Rappresenta
una circonferenza
in 4 dimensioni
Questa scelta, come al solito,
nasconde la simmetria.
Il meccanismo per far quadrare i conti è lo stesso di quello visto nel caso U(1):
possiamo scegliere la direzione degli assi di isospin in ogni punto x dello spaziotempo per allineare f(x) lungo la direzione scelta, effettuando una rotazione SU(2)
diversa a seconda di x.
Il campo, scritto nella forma “esponenziale * fase”, può essere ridotto scegliendo la
gauge in funzione di x, come visto prima:
f ( x)
0
1
iq ( x )
exp
2 v H ( x)
2v
q’=q+v
i ( x )
f ( x) f ' ( x) exp
f ( x)
2
0
0
iq ' ( x )
i[v ( x) q ( x)]
exp
exp
2v v H ( x)
v
H
(
x
)
2v
Con =-q/v la fase si annulla, come prima, e i bosoni di Goldstone spariscono.
Inserendo nella Lagragiana l’espansione di f intorno al vuoto, si arriva dopo un po’ di
conti a:
2 2
1
g
v
1
2
3
2
2
2
L [ ( H ) lv H ]
[(W ) 2 (W ) 2 (W ) 2 ] ...
2
8
E’ chiaro che L descrive un campo massivo con mH=(2lv2)½ e tre campi di gauge
massivi con mW= ½ gv.
La Lagrangiana del Modello Standard
Il passo finale per scrivere una Lagrangiana delle interazioni elettrodeboli con tre
bosoni vettori massivi e un fotone a massa nulla consiste nel considerare il
gruppo SU(2)LxU(1)Y e richiedere l’invarianza di gauge locale indipendentemente
ai due sottogruppi.
(NB: qui I / 2 )
Per campi fermionici L si scrive allora
L Lg [i gI W
g'
g'
YB ] L Rg [i YB ] R ...
2
2
In questa formulazione tutti i campi hanno ancora massa nulla. Termini di massa
per i fermioni rompono anch’essi l’invarianza di gauge di SU(2)L.
Aggiungendo a L i termini relativi a un doppietto di scalari complessi in forma di
doppietto di isospin debole con ipercarica Y=+1,
L (Df )† (Df ) 2f †f l (f †f )2
con la derivata covariante
f
1 f1 if2
f ( 0)
(f if )
f
2 3
4
D [i gI W ( g ' / 2)YB ]
0
1
f ( x)
2 v H ( x)
troviamo che la Lagrangiana dei campi bosonici contiene ora i termini
e scegliendo il vuoto e la sua espansione come al solito,
(
)
1
g 2v 2
v2
1 2
2 2
3
2
2
2
L [ ( H ) lv H ]
[(W ) (W ) ] ( gW g ' B )( gW 3 g ' B ) ...
2
8
8
I campi W3 e B sono mescolati dalla scelta della gauge unitaria. Possiamo
3
disaccoppiarli con la combinazione lineare
A B cos q W sin q
W
W
Z B sin qW W cos qW
dove abbiamo anche definito tan(qW )=g’/g. Con questa sostituzione si trova
(sempre trascurando i termini di interazione):
1
L ( H ) 2 lv 2 H 2
2
La rottura di
SU(2)xU(1) ha dato
1
g 2v 2
1
1
1
1
1
( W W )( W W )
(W ) 2
vita precisamente allo
4
8
spettro che volevamo:
1
g 2v 2
2
2
2 2
2
2
( W W )( W W )
(W )
un bosone scalare
4
8
massivo, due W e
2
1
v
una Z massivi, e un
( Z Z )( Z Z ) ( g 2 g '2 ) Z Z
4
8
fotone a massa nulla.
1
( A A )( A A ) ...
4
3
All’inizio avevamo 8 gradi di libertà dai bosoni vettori e 4 dal doppietto scalare U(1) con Y=1, lo
scalare di Higgs. Ora abbiamo tre bosoni massivi (3x3=9 gradi di libertà), uno massless (2 g.l.)
e un bosone scalare di Higgs. I conti tornano!
Con la scelta Y=1 per il doppietto scalare di Higgs, esso ha due componenti, una carica (Q=1) a
I3= ½ e una neutra (Q=0) a I3=- ½ perché Q=I3+Y/2. E’ chiaro che solo la componente neutra
può assumere un v.e.v. non nullo – le fluttuazioni del vuoto non generano carica!
E il termine di interazione...
La parte di interazione fra fermioni e campi vettoriali, introdotta dalla derivata
covariante, si può scrivere in forma compatta come
g'
i[ gj W
,3
,3
,3
2
j B]
Il disaccoppiamento dei termini di campo neutri W3, B avviene attraverso la
rottura di simmetria, che li mescola in una combinazione lineare massless (il
fotone) e una massiva (lo Z):
W A sin q Z cosq
,3
W
B A cosq Z sin q
W
W
W
qW , introdotto da Glashow, è detto angolo di Weinberg, sin2qW=0.23 .
termine della corrente
debole neutra
Dal termine di interazione otteniamo:
g'
j
i[ gj W j B ] i ( g sin q j g ' cosq
) A (...)Z
2
2
,3
,3
,3
W
3
Y
W
Si vede quindi, dato che Q=I3+Y/2, che la corrente elettromagnetica che
otteniamo è consistente con quella che conosciamo dalla QED se poniamo
g sin q g ' cosq e
W
tanq g ' / g
W
W
Considerazioni aggiuntive
•
Possiamo trovare una simmetria residua del vuoto, descritta da un sottogruppo del gruppo
SU(2) LxU(1)Y ? In tal caso il bosone di gauge associato rimane a m=0, come sempre.
In effetti se applichiamo Q allo stato di vuoto
f
0
1 0
2 v
troviamo Qf0=(I3+Y/2) f0=0 per cui il vuoto che abbiamo scelto è effettivamente invariante
per una U(1) locale generata da Q:
f0 f '0 eia( x )Qf0 f0
•
Dei quattro generatori I e Y, solo la combinazione Q lascia il vuoto invariante. U(1)Q è un
sottogruppo di SU(2)LxU(1)Y. Il fatto che il fotone rimanga a massa nulla non è una previsione
del modello, ma è implicita nella scelta di uno stato di vuoto a carica nulla..
•
Usando la massa MW= ½ gv, e il valore misurato della costante di Fermi e della costante di
struttura fine, troviamo:
2
dall’elemento di
matrice di corrente
carica per q0
•
•
g
G
8mW2
2
, mW
1
vg v ( 2G) -1/2 246GeV
2
a
g sin qW e , a e 2 / 4 mW
2
G
mW 80GeV , mZ mW / cos qW 90GeV
1/2
1
sin qW
La massa del bosone di Higgs dipende dal parametro lambda, e non è prevista dal modello.
Vedremo che v è curiosamente vicino a 2½ Mtop più avanti…
La massa dei fermioni
prodotto di
doppietti e
di singoletti
di SU(2)
non gauge-invariante
La Lagrangiana dei campi di Dirac
L Lg [i gI W
g'
g'
YB ] L Rg [i YB ] R ...
2
2
non ammette termini di massa per i fermioni, se si vuole mantenere l’invarianza di
gauge. Per campi di Dirac i termini di massa sono scrivibili come
5
5
1
1
m e e m e [ (1 g ) (1 g )] e m( R L L R )
2
2
I
Se ricordiamo le assegnazioni di isospin e ipercarica debole:
Y
e 1/ 2 1/ 2 1
vediamo che il doppietto scalare scelto per descrivere
il campo di Higgs ha proprio i valori “giusti” per
H(I= ½,Y=1)
accoppiare fermioni left e right:
eL 1 / 2 1 / 2
1
eR
2
0
0
eL(I= ½,Y=-1)
eR(I=0,Y=-2)
Possiamo allora aggiungere alla Lagrangiana
il termine gauge-invariante
I3
f
0 e
g e [( e , e) L 0 eR e R f , f ]
e L
f
Scegliendo il vuoto e le sue fluttuazioni come al solito, la Lagrangiana viene a
contenere termini del tipo
ge
ge
v(eL eR eR eL )
(eL eR eR eL )h
2
2
ove è facile identificare con la massa dell’elettrone il termine
Abbiamo sostituito
a (f+,f0) l’espressione
nell’intorno del vuoto
scelto
gev
me
me
Lm me ee
eeh
v
2
In L notiamo anche il termine di accoppiamento di H al campo fermionico: esso
è proporzionale alla massa del fermione.
Questo fatto è importante per capire la fenomenologia del bosone di Higgs (lo
vedremo nella seconda parte di questo capitolo).
Va notato che il meccanismo di Higgs, che ci è servito a dotare di massa i
bosoni vettori W e Z – ottenendo una teoria rinormalizzabile e coerente – ci
“regala” automaticamente termini di massa anche per i fermioni. Assieme a
questi abbiamo dovuto comprare anche i termini di accoppiamento, che infatti
sono proporzionali a m (m=0 zero accoppiamento)
Tuttavia, i valori delle masse sono arbitrari, e rimangono parametri della teoria.
Notare che i neutrini sono solo
left-handed per cui non possiamo
mettere un termine di massa!
Una rivisitazione delle divergenze
•
Il meccanismo di Higgs è un metodo elegante per introdurre bosoni massivi
nella teoria, ma non sarebbe obbligatorio se non fosse per la
rinormalizzabilità della teoria
•
Abbiamo già notato come i processi di scattering di neutrino su elettrone
siano divergenti se non si include lo scambio di un bosone massivo W
•
L’introduzione dei W a sua volta comporta problemi, in quanto si dimostra
che lo scattering neutrino-W (un processo praticamente impossibile da
generare, ma teoricamente lecito) diverge. Serve un altro diagramma con
scambio di Z per rendere la somma convergente!
•
La soluzione non è unica, ma l’arrangiamento dei bosoni deboli in una
struttura gruppale SU(2) è elegante e economica
•
Lo scattering WWWW mostra come il bosone di Higgs entra direttamente
in gioco rendendo convergente il processo. Senza un bosone scalare H
accoppiato ai W non ci sarebbe rinormalizzabilità della teoria GSW!
Masse e accoppiamenti
• Quanto visto sopra per i termini di massa dei leptoni carichi si può
estendere ai quarks: le masse di questi dipendono anch’esse dal
valore di v e da costanti incognite g.
• In termini del v.e.v. del campo di Higgs, sviluppando il termine
quadratico negli spinori le masse dei fermioni si scrivono
mf = 2-½ gfv.
• I valori degli “accoppiamenti di Yukawa” gf dell’Higgs ai fermioni
coprono un vasto range di valori:
g u 2 105
g c 9 103
gt
g d 4 105
g s 8 104
g b 3 102
g e 3 106
g 6 104
g 1102
1
• Il Modello Standard non solo non predice il valore dei parametri g,
ma non ne spiega l’ampio range.
• Inoltre, la quasi esatta coincidenza di gt con 1 è un’osservazione di
grande interesse…
Esercizio per casa n°5
Partendo dalla parte di interazione nel termine cinetico del campo scalare espresso
per mezzo della derivata covariante SU(2)xU(1):
D [i gI W ( g ' / 2)YB ]
sostituire il campo scalare nell’intorno del vuoto ,
0
1
f ( x)
2 v H ( x)
(
)
arrivando ad esprimere i termini di massa e di interazione per mezzo degli stati
ruotati relativi ai bosoni fisici W+,W-,Z, e ottenere i termini di massa e accoppiamenti
del W,Z, e fotone. Commentare sulle intensità relative e la presenza o assenza di
termini relativi agli accoppiamenti fra queste particelle, e le implicazioni.
Ricordando che le larghezze sono proporzionali al quadrato degli accoppiamenti al
vertice, usare i valori ottenuti per prevedere il rapporto fra le larghezze di
decadimento
G( H WW )
G( H ZZ )
(Hint: il termine da sviluppare è
usando anche:
1 1
2
W 2 (W iW )
W 1 (W 1 iW 2 )
2
g'
1
0
( g W B )
2
2
2 v H ( x)
e le relazioni fra A,Z e B,W3)
2