Il Settore di Higgs
del Modello Standard
Università di Padova
Corso Fisica Subnucleare - II anno laurea specialistica
Simonetto/Dorigo, AA 2008/09
Tommaso Dorigo
[email protected]
Stanza 3L0, tel. 049-8277230, 349-7267845.
http://dorigo.wordpress.com
Sommario
•
PARTE I: La lagrangiana del Modello Standard
–
–
–
–
–
–
–
•
Introduzione alle simmetrie di gauge
Simmetrie esatte, rotte, nascoste
Il teorema di Goldstone
Rottura della simmetria di gauge e meccanismo di Higgs
Lagrangiana del Modello Standard
Accoppiamenti, masse e implicazioni
La running coupling constant della QCD
PARTE II: Fenomenologia del bosone di Higgs e ricerche sperimentali
–
–
–
–
–
–
–
Considerazioni teoriche
Correzioni radiative e constraints da fit elettrodeboli
Decadimenti
Meccanismi di produzione in collisioni elettrone-positrone
Meccanismi di produzione ai colliders adronici
Ricerche dirette a LEP II e limiti sperimentali
Ricerche del bosone di Higgs al Tevatron
•
•
•
•
–
Apparati sperimentali: CDF e D0
Sezioni d’urto, stati finali accessibili
Tecniche sperimentali
Qualche esempio in dettaglio
Prospettive della ricerca a LHC
•
•
Produzione a LHC e stati finali promettenti
Tecniche di ricerca e prospettive
Testi consigliati
•
F.Halzen, A.D.Martin, “Quarks & Leptons: An Introductory Course in Modern
Particle Physics”, Wiley 1984
– Cap.14,15
•
W.E.Burcham,M.Jobes, “Nuclear and Particle Physics”, Longman 1995
– Cap.13
•
R.K.Ellis, W.J.Stirling, B.R.Webber “QCD and Collider Physics”, Cambridge
U.P. 1996
– Cap. 8, 10, 11
•
Altri testi utili (livello più avanzato):
– L.B.Okun, “Leptoni e Quarks”, Ed. Riuniti 1986
• Cap.19,20
– F.Mandl, G.Shaw, “Quantum Field Theory”, Wiley 1984
• Cap. 11,12,13
– J.F.Donoghue,E.Golowich,B.R.Holstein “Dynamics of the Standard Model”,
Cambridge U.P. 1992
• Cap.15
A word of warning
• Non sono un’enciclopedia
– Dimentico cose, a volte (raramente) dico fesserie – la maggior parte
delle volte mi correggo, dopo.
– A volte potrò dimenticare di spiegarvi con chiarezza dove sto andando a
parare: se sentite qualche argomentazione di cui non capite l’origine o
l’arrivo, e non vi siete appena svegliati, fermatemi.
• Non sono un teorico
– La mia conoscenza dei calcoli teorici soggiacenti ad alcune parti della
trattazione è arrugginita
• Avrete una prospettiva “sperimentale” degli argomenti
• Per fortuna molti di voi seguono il corso di Feruglio!
– Mi potrà capitare di non saper o non voler rispondere a qualche
domanda ben congegnata:
• menzione onorevole se si tratta di un punto rilevante, e risponderò alla
lezione successiva;
• altrimenti verrete ignorati se i concetti necessari sono al di là dello scopo del
corso.
• Sono qui per migliorare, come voi
– Voi imparate quello che spiego (spero), io imparo a spiegarlo meglio– a
vostre spese
• Ogni critica è bene accetta se costruttiva…
Inoltre:
• A volte andrò molto veloce
– E’ un segno che considero quello che vedete nelle slides cose già note,
non che devo prendere il treno!
• Se non riuscite a seguirmi potete interrompermi, e in genere vi darò ascolto
– ma vi potrei anche dire di riguardarvi il materiale per conto vostro
• A volte ripeterò i concetti più volte
– Segno che vorrei li apprezzaste e che ve li chiedero’ all’esame
• A volte salterò qualche slide
– Potrebbe servirmi ad arrivare in fondo a una lezione, con l’impegno di
tornarci al momento opportuno
– Oppure può darsi che si tratti di materiale superfluo
• Tutte le slides che vedrete saranno disponibili in rete a fine corso
– Non prima perché intendo rivederle dopo averle presentate
– Le slides sono verbose per vostro comodo – dovrebbero risultare
leggibili e aiutare chi ha perso una lezione a ricostruirne il percorso
• In verde ci sono alcuni esercizi per casa
– Dovrebbero essere alla vostra portata – non spaventatevi!
– Per stimolarvi, non ve ne darò soluzione immediatamente, ma potrete
venire a discuterli con me
– In ogni caso sono risolti qua e là nei testi citati.
PARTE I
• La lagrangiana del Modello Standard
–
–
–
–
Introduzione alle simmetrie di gauge
Simmetrie esatte, rotte, nascoste
Il teorema di Goldstone
Rottura della simmetria di gauge e meccanismo di
Higgs
– Lagrangiana del Modello Standard
– Accoppiamenti, masse e implicazioni
– La running coupling constant della QCD
Introduzione:
Simmetrie di gauge e MS
A bassa energia le interazioni forte, em e debole sembrano indipendenti: hanno
sezioni d’urto che differiscono di 12 ordini di grandezza diverse costanti di
accoppiamento
La speranza di descrivere queste interazioni con un unico campo unificato, ad
alta energia, ricevette verso la fine degli anni ’60 una spinta dalla formulazione
GSW (Glashow, Salam, Weinberg) dell’unificazione elettrodebole.
Il passo teorico più importante in questa direzione è realizzare che le interazioni
fondamentali sono invarianti per trasformazioni locali di gauge
Per formulare una teoria di gauge bisogna scrivere una lagrangiana che descriva
la cinematica e le interazioni fra i campi, e sia invariante sotto trasformazioni di
simmetria che permettano la conservazione delle quantità rilevanti: carica
elettrica, colore, isospin e ipercarica deboli. Queste quantità sono conservate
localmente, per non entrare in conflitto con la relatività speciale.
La formulazione lagrangiana ha il vantaggio che dallo studio delle proprietà
invarianti di L si arriva naturalmente alle quantità conservate della teoria. La
connessione per trasformazioni continue è data dal teorema di Noether.
• Invarianza globale di gauge conservazione carica elettrica
• L’imposizione di invarianza locale di gauge per la lagrangiana di un
campo di Dirac forza l’introduzione di una derivata covariante, e un
campo di gauge Am associato al fotone. Si ottiene la lagrangiana di
QED
• Invarianza locale di gauge introduzione di un campo vettoriale a
massa nulla (consistente con il range infinito dell’interazione). Un
termine di massa per il fotone romperebbe l’invarianza di gauge per
via delle proprietà di trasformazione del campo Am.
• Questo vale per qualunque bosone vettore. I bosoni deboli non
sfuggono alla logica. Se vogliamo invarianza locale di gauge, i
bosoni rimangono a massa nulla.
Invarianza di gauge globale
La lagrangiana di elettrone libero
L (i m m m)
è invariante per trasformazioni U(1) globali
se vale
' eiqL
0 L 2qL m ( m )
per arbitrari valori della fase globale L.
(Es. n.1 per casa: dimostrare l’affermazione qui sopra, usando le
equazioni di Eulero - Lagrange)
Ciò implica la conservazione di una quadricorrente
m j m m (q m ) 0
e quindi della carica elettrica q, integrando nelle coordinate spaziali
e usando il teorema della divergenza:
q j d x
0
3
dq
a j a d 3 x j ds 0
dt
a 1, 3V
S
Invarianza di gauge locale e QED
La lagrangiana di elettrone libero
L (i m m m)
rimane invariante per trasformazioni U(1) locali
' eiqL ( x )
solo se si introduce una corrispondente variazione nella legge di trasformazione
delle derivate del campo fermionico, una derivata covariante
definita da
Dm eiqL ( x ) Dm
Dm m iqAm (x)
in cui il campo vettoriale A trasforma come segue:
Am ( x) Am ( x) m L( x)
La lagrangiana che deriva dall’inserimento della derivata covariante D contiene ora
un termine di accoppiamento della corrente vettoriale e il campo A:
L i m m m qAm m
Il termine cinetico del campo A è invariante per la trasformazione vista, ma un
termine m2AmAm non è permesso perché non trasforma in se stesso: l’invarianza
locale di gauge richiede che la carica conservata sia sorgente di un campo
vettoriale privo di massa.
•
•
In contrasto con la richiesta formale di bosoni massless nella teoria, l’esistenza di
correnti deboli cariche mediate da bosoni vettori massivi è necessaria per evitare
divergenze nelle sezioni d’urto di scattering.
Esempio: ne-e scattering s prop. a G2s,
n
n
n
mentre l’unitarietà dello sviluppo in onde
W
parziali della sezione d’urto (J=1) implica
e
e
e
che s sia minore di 1/s per
s>1/G =9E4GeV2 la sezione d’urto
g 2 / M W2
GF / 2
viola l’unitarietà.
Invece, se il propagatore del W contiene un termine di massa, esso rende finita la
sezione d’urto.
•
Violazione dell’unitarietà nei diagrammi all’ordine più basso e non rinormalizzabilità
dei diagrammi ad ordini superiori sono strettamente legate: l’una implica l’altra.
•
In ogni caso, due bosoni W+ e W- non bastano a rendere la teoria consistente: la
sezione d’urto del processo di produzione di coppie WW rimane divergente, sia per
interazione debole nnWW che e.m. eeWW.
e
n
•
La divergenza del processo nnWW si può neutralizzare con diagrammi
mediati da un bosone neutro massivo Z. Esso permette anche di
neutralizzare la divergenza del processo elettromagnetico, mediante
diagrammi che singolarmente sono divergenti.
– NB: La predizione di processi con correnti deboli neutre (come lo scattering nme), che –se mediati da scambio di un solo bosone vettore dovevano avere
sezioni d’urto comparabili a quelli con scambio di corrente carica (come ne-e)- fu
uno dei grandi successi della teoria elettrodebole.
•
La cancellazione è possibile solo se gli accoppiamenti ai leptoni dei bosoni
W,Z, sono di intensità confrontabile: g ~ e.
•
Questa unificazione elettrodebole necessita che W e Z abbiano masse
dell’ordine dei 100 GeV. Ciò apparentemente è in conflitto con l’invarianza
locale di gauge della lagrangiana.
•
Vedremo che l’introduzione di un campo scalare h e un meccanismo
appropriato risolvono il problema. In più, h permette la convergenza dello
scattering WWWW, che rimaneva divergente (anche se in maniera meno
severa degli altri processi discussi sopra).
Ma perché insistere con la gauge locale?
Sia i fotoni che i gluoni hanno massa nulla, e questo si sposa bene con la struttura delle
rispettive lagrangiane con invarianza di gauge.
Per le interazioni deboli, che richiedono bosoni vettori di massa O(100 GeV), questo è invece
un problema. Ma perché non dimenticarsi dell’invarianza locale e aggiungere a L termini di
massa?
Se si fa questo, si finisce in una teoria senza senso, perché ogni quantità calcolabile da essa
conterrà divergenze non rinormalizzabili.
Esempio: nello scattering fra due elettroni
si hanno diagrammi come quello a fianco.
e
Essi contribuiscono all’ampiezza con
integrali del tipo
4
q
Z
Z
d
q ( propagatori )
e
Mentre in QED la forma 1/q2 del propagatore dei due fotoni scambiati rende finito l’integrale,
per bosoni massivi il risultato diverge, data la costanza del propagatore a q2 grande:
i
g mn qm qn / M 2
q M
2
2
q
2
iq m qn
q2M 2
Se poi si regolarizza l’integrale introducendo un cut-off, si scopre che altri diagrammi con più
loops richiedono altrettanti cut-offs indipendenti. Serve quindi un numero infinito di parametri
arbitrari, e la teoria non ha più senso: essa è non rinormalizzabile.
Rottura spontanea di una simmetria discreta
Consideriamo la lagrangiana
L T V
1
1
1
( mf ) 2 ( m 2f 2 lf 4 )
2
2
4
Con l>0, essa possiede una simmetria discreta rispetto all’operazione di
riflessione f -f.
Se prendiamo m2>0, L descrive una particella a spin 0 e massa m; il
termine quartico nel campo dètta l’autointerazione del campo con vertici
a 4 particelle, con un autoaccoppiamento di intensità l.
Invece, se prendiamo m2<0, non sappiamo come interpretare il
termine f2, perché la massa della particella sarebbe immaginaria.
La forma del potenziale nei due casi
è mostrata a lato. Mentre per m2>0 lo
stato f=0 è un minimo, nel caso m2<0
il minimo del potenziale si ha per
f v m2 / l
Poiché in fisica delle particelle non siamo in grado di calcolare la fisica
esattamente, ma dobbiamo ricorrere a espansioni perturbative attorno
a un minimo del potenziale,
è opportuno operare una traslazione del campo attorno al minimo:
f ( x) v h ( x)
Si ottiene allora una nuova forma per L (che descrive la stessa fisica!):
L'
1
1
( mh ) 2 l v 2 h 2 l vh 3 lh 4
2
4
Questa lagrangiana ha un termine di massa del segno corretto per la
fluttuazione h(x), mentre i termini di ordine superiore in h
rappresentano le autointerazioni del campo.
La massa del campo scalare è ricavabile dal termine quadratico:
mh 2l v2 2m 2
Abbiamo quindi scoperto che nel caso m2<0 L e L’ rappresentano in
effetti un campo scalare massivo. In teoria delle perturbazioni L’
fornisce risultati sensati, mentre L no, perché espansioni perturbative
attorno a f=0 non convergerebbero.
Alcune considerazioni sulla “rottura” di simmetria
•
•
La traslazione operata nel campo, che trasforma L in L’, rende nascosta la simmetria:
intorno al punto di minima energia L’ non è più in variante per trasformazioni f-f.
E’ la presenza di una degenerazione nello stato di vuoto che rende arbitraria la scelta di
esso, e di conseguenza nasconde la simmetria originale di L.
•
Tuttavia per valori grandi dell’energia (rispetto alla massa del campo), la teoria ritorna ad
avere la sua simmetria per riflessione: in quel caso, la massa della fluttuazione quantistica
h(x) non è più rilevante per determinare la fisica, e la simmetria ritorna ad essere
apparente.
•
Vi sono in natura diversi sistemi che manifestano lo stesso meccanismo. Sono tutti esempi
della stessa situazione: casi in cui è energeticamente favorevole per lo stato fondamentale
avere un valore non nullo di un campo.
•
Consideriamo V(f) = ½ m2f2 + ¼ lf4 : i due minimi degeneri si trovano a V<0. Con
l’aggiunta di una costante (che non cambia l’equazione dei campi!) si può riscrivere V in
modo che il vuoto si trovi a V’=0:
V’(f) = ¼ m4/l ½ m2f2 ¼ lf4 ¼ l(f2m2/l)2.
Dai dati sull’espansione dell’universo, l’energia del vuoto è sì negativa, ma estremamente
piccola rispetto al valore indicato da V, che per l1, m=1 GeV vale 1041 GeV/cm3 (da
confrontare con 10-6GeV/cm3 che e’l’energia media dell’universo).
Dunque è opportuno considerare V’ invece di V.
Simmetrie esatte, nascoste, e rotte
A seconda della dinamica della teoria, le simmetrie della funzione L possono
manifestarsi in molti modi diversi.
– Una simmetria di L rimane una simmetia della fisica che ne ha origine. Esempi sono
SU(3) di colore o U(1) elettromagnetica
– La simmetria di L è solo apparente, perché in realtà essa ha un’anomalia. U(1) assiale è
un esempio nello SM. Un’anomalia avviene quando una simmetria delll’azione non è una
vera simmetria della teoria quantistica corrispondente. Non ce ne occupiamo in questo
corso (a parte un accenno nell’introduzione al top quark).
– La simmetria di L può essere rotta esplicitamente da termini non invarianti. Un esempio è
la simmetria di Isospin SU(2) tra u e d, che è rotta dall’elettromagnetismo e dalla
differenza di massa dei due quarks. E’ una simmetria approssimativa.
– La simmetria di L può infine essere nascosta, ovvero l’operazione può lasciare L
invariante ma modificare lo stato fondamentale. In questo caso non è apparente la
simmetria nello spettro degli stati fisici. Ci sono due modi in cui questo può accadere:
• Uno o più campi scalari acquistano valori diversi da zero nel vuoto: si tratta di rottura spontanea
di simmetria, il cui esempio più lampante è SU(2)L rotta dal campo di Higgs nelle interazioni
deboli
• Quando sono effetti quantistici non presenti nella lagrangiana classica a rompere dinamicamente
la simmetria, non si osservano corrispondenti campi scalari. Un esempio è la rottura della
simmetria chirale di QCD, SU(2)LxSU(2)R.
Il teorema di Goldstone
Consideriamo ora un campo scalare complesso
e dunque la forma
f
1
(f1 if2 )
2
L ( mf )* ( mf ) m 2f *f l (f *f )2
L è in questo caso invariante per una trasformazione di fase globale feiaf :
possiede una simmetria per trasformazioni U(1) e la fisica non dipende da a.
Prendiamo l>0, m2<0 ed esplicitiamo la dipendenza di L dalle componenti reale e
immaginaria di f:
1
1
1 2 2
1
2
2
2
2
2
L ( mf1 ) ( mf2 ) m (f1 f2 ) l (f1 f2 ) 2
2
2
2
4
Si vede che in questa formulazione il potenziale V(f) ha un minimo per tutti i
valori del campo tali che f12+f22 = v2 = -m2/l .
Questa volta abbiamo un’infinità continua di minimi per V, organizzati in una
circonferenza di raggio v attorno a f=0. Come nel caso scalare reale, ci troviamo
nella necessità di scegliere un valore del minimo attorno al quale operare i calcoli
perturbativi per estrarre la dinamica di f da L.
Scegliamo espansioni intorno al vuoto f1=v, f2=0 scrivendo
f(x) = [v+h (x)+ix (x)]/2½
e sostituiamo l’espressione in L. Otteniamo una nuova forma L’:
L'
1
1
( m x ) 2 ( mh ) 2 m 2h 2 c (h 3 ) (hx 2 ) (h 4 ) (x 4 ) (h 2x 2 )
2
2
ove si sono espressi in forma concisa i coefficienti nei termini di
autointerazione dei campi.
Espressa con x e h L’ possiede due termini cinetici ma un termine di massa
solo per h:
2
mh 2m
Il campo x tangenziale alla circonferenza di minimo potenziale non incorre in
resistenza dal potenziale per piccole oscillazioni intorno al minimo (v,0), e
rimane a massa nulla. E’ la presenza di una degenerazione dello stato di
vuoto a mantenere nulla la sua massa.
La rottura della simmetria di L ha apparentemente avuto un effetto nefasto,
in quanto oltre al campo massivo h che volevamo generare, compare uno
scalare massless, h. h è detto bosone di Goldstone.
Il caso considerato è solo un caso particolare di un teorema generale, il
teorema di Goldstone: la rottura spontanea di una simmetria continua
genera bosoni scalari a massa nulla.
Esercizio per casa n°2: dimostrare che la lagrangiana per tre
campi scalari interagenti
2
1
m
L mf i mfi
fifi l (fifi ) 2
2
2
descrive un campo scalare massivo e due campi scalari a massa
nulla.
(Hint: trovare l’espressione del minimo del potenziale, e
scegliere opportunamente il valore del campo nei
dintorni del vuoto.)
Quanto visto sembra implicare che la strada che stiamo investigando per
dotare la nostra teoria elettrodebole di bosoni massivi è destinata a
fallire, in quanto oltre ai bosoni massivi si generano campi scalari a
massa nulla che non si osservano in natura: non esistono particelle
scalari a m=0!
Tuttavia, vedremo che succede qualcosa di diverso quando si applica il
meccanismo di Goldstone alla lagrangiana SU(2)xU(1) del modello
elettrodebole.
Il meccanismo di Higgs
Il modello di Goldstone ora visto si può dotare dell’interazione
elettromagnetica tenendo presente il principio di gauge e passando a
una simmetria U(1) locale:
1
L ( m iqAm )f * ( m iqA m )f m 2f f l (f f ) 2 Fmn F mn
4
Fmn m An n Am
Prendendo lo stato di vuoto in (v,0) e scegliendo l’espansione
la lagrangiana diventa
f1 v h ( x)
f2 x ( x )
1
1
1
1
L ( mh )( mh ) lv 2h 2 ( m x )( mx ) q 2 v 2 Am Am qvAm m x Fmv F mv ...
4
2
2
2
C’è una difficoltà rispetto a prima: il campo scalare h ha ora massa
(2lv2)1/2 , x è rimasto a massa nulla, e il campo di gauge Am ha massa
qv: questo corrisponde a un grado di libertà in più rispetto alla
lagrangiana di partenza!
Il grado di libertà in più è però fittizio. Il campo x è in effetti irrilevante
per la fisica, e possiamo scegliere un particolare forma per la
trasformazione di gauge che lo elimini.
Scriviamo allora il campo nella forma modulo*exp(fase):
f ( x)
1
[v H ( x)]e[iq ( x ) / v ]
2
Se ora applichiamo al campo una gauge locale U(1) abbiamo
f ' ( x) e[iqL ( x )]f ( x)
Il che significa che dobbiamo avere
[v H ' ( x)]e[iq '( x ) / v ] e[iqL ( x )][v H ( x)]e[iq ( x ) / v ]
Da ciò segue che le fluttuazioni H’ e q’ devono trasformare come:
H ' ( x) H ( x)
q ' ( x) q ( x) qvL ( x)
E’ quindi chiaro che scegliendo la fase
1
L( x) q ( x)
qv
NB: nel caso del campo scalare complesso
con L invariante per U(1) globale eia, nessuna
scelta della fase costante a può cancellare
Il campo x(x), qui invece la simmetria per
fasi L(x) dipendenti da x ce lo permette!
(chiamata gauge unitaria) abbiamo q’(x)=0. I bosoni di Goldstone
corrispondono ai quanti del campo q(x): attraverso la scelta della gauge, li
abbiamo eliminati dallo spettro della teoria!
E’ chiaro che i bosoni di Goldstone sono “oscillazioni” nel parametro
che distingue diversi stati di vuoto: la fase qL(x). Scegliendo la gauge
unitaria abbiamo rimosso il grado di libertà non voluto.
Usando le regole di trasformazione del campo scalare e del campo di
gauge per U(1) locale, con la scelta della fase vista sopra:
1
Am ' ( x) Am ( x ) mq ( x)
qv
1
[v H ( x )]
2
possiamo allora riscrivere la lagrangiana:
1
1
1
L [ ( m H ) 2 lv 2 H 2 ] q 2 v 2 Am Am q 2 Am Am H 2
2
2
2
1
1
1 4
2
m
3
4
mv
q vAm A H lvH lH Fmv F lv
4
4
4
Come promesso, L non contiene traccia della fase q(x).
f ' ( x)
La trasformazione di L in una forma che esplicita il trasferimento di
gradi di libertà associati a bosoni di Goldstone a componenti
longitudinali di bosoni vettori è noto come meccanismo di Higgs.
Quello visto sopra è il caso U(1).
Trasformazioni SU(2) e Yang-Mills
•
Per introdurre il modello standard conviene prendere in considerazione due campi di Dirac
che trasformino come un doppietto per una simmetria interna SU(2) di isospin.
m
1
m
L (i m)
•
•
•
( )
2
Richiediamo che la lagrangiana sia in variante per trasformazioni SU(2) locali infinitesime:
' e
[1 igL / 2]
igL / 2
I generatori di SU(2) non commutano (il gruppo non è abeliano):
i j
[
,
2 2
] i ijk
k
2
In analogia con la QED possiamo richiedere la gauge invarianza locale usando derivate
covarianti:
Dm m ig
j
2
Wmj
Wm Wm
1
m L gL Wm
g
•
I campi W devono trasformare come segue:
•
Il termine cinetico dei campi contiene ora un’autointerazione dei W, in quanto
Wmn mWn n Wm gWm Wn
•
La lagrangiana è invariante per SU(2) locali ma non ammette un termine di massa per i W.
Le teorie di Yang-Mills richiedono l’esistenza di campi vettoriali a massa nulla.
Il meccanismo di Higgs in SU(2)
Prendiamo ora in considerazione la rottura spontanea della simmetria locale di
gauge del gruppo SU(2)L. Questo gruppo non è scelto a caso, ma è il punto di arrivo
dell’indagine di Glashow, Salam e Weinberg per inserire in una teoria di gauge i
bosoni vettori massivi W. Il fotone arriverà includendo U(1)...
Si parte da una lagrangiana che descrive un doppietto di campi scalari: 4 gradi di
libertà. Ci servono 3 di essi per dotare i bosoni vettori della teoria GSW di massa…
L ( mf )† ( mf ) m 2f †f l (f †f )2
fa
1 f1 if2
Scriviamo i campi come segue:
f ( )
(
)
fb
2 f3 if4
Sotto una trasformazione SU(2) globale dei campi f,
f f' e
(
iL j j
2
)
f
L è chiaramente invariante. Per renderla localmente invariante introduciamo un
parametro di gauge L(x) e rimpiazziamo la
j j
derivata con una covariante:
Dm m ig
W è un tripletto di campi di gauge
e per rotazioni infinitesime di SU(2)
trasforma come
Wm Wm
Wm
2
f ( x) f ' ( x) [1 L( x) / 2]f ( x)
1
m L L Wm
g
Con l’introduzione della derivata covariante, la lagrangiana diventa
L ( mf ig
2
Wmf )† ( mf ig
1
W mf ) V (f ) WmnW mn
2
4
L’ultimo termine rappresenta l’energia cinetica dei campi di gauge,
prodotto dei tre tensori Wmn:
Wmn mWn n Wm gWm Wn
Se ora poniamo come al solito l>0, m2<0, il potenziale V (f ) m 2f †f l (f †f ) 2
ha un minimo in
1 2
v2
* * fa
*
*
2
2
2
†
f f (fa fb )( ) fa fa fb fb (f1 f2 f3 f4 )
fb
2
2
Scegliamo ora f32=v2, “nascondendo” la simmetria SU(2) nello stato di vuoto. Possiamo allora
espandere il campo nell’intorno del vuoto scelto,
scegliendo una fase tale che
0
1
f ( x)
2
(v H ( x))
NB vedi prossima slide
Il meccanismo è lo stesso di quello visto nel caso U(1): possiamo scegliere la direzione degli
assi di isospin in ogni punto x dello spazio-tempo per allineare f(x) lungo la direzione scelta,
effettuando una rotazione SU(2) diversa a seconda di x. Il campo, scritto nella forma
“esponenziale * fase”, può essere ridotto scegliendo la gauge, come visto prima.
Inserendo nella lagragiana l’espansione di f intorno al vuoto, troviamo
1
g 2v 2
1
2
3
2
2
2
L [ ( m H ) lv H ]
[(Wm ) 2 (Wm ) 2 (Wm ) 2 ] ...
2
8
E’ ora chiaro che L descrive un campo massivo con mH=(2lv2)½ e tra campi di gauge massivi
con mW= ½ gv.
Sulla generalità della scelta del
vuoto
Lo sviluppo nell’intorno del vuoto
1 0
f0
2 v
()
si può effettuare con i quattro campi reali q1,q2,q3,h attraverso la formulazione
0
1
f ( x)
2 v h( x )
(
i q ( x ) / v
)e
Questo è perfettamente generale in quanto, per piccole perturbazioni,
i (q iq ) / v
0
1 1 iq / v
f ( x)
)
(
1 iq / v v h ( x )
2 i (q iq ) / v
3
1
1 q iq
2 v h iq
2
1
2
1
3
2
3
Un richiamo: l’ipercarica debole
•
Se si scrivono le correnti deboli cariche
jm n L m eL
jm e L mn L
•
con le matrici di Pauli operanti su doppietti di fermioni left-handed, si hanno correnti chargeraising e charge-lowering:
jm L m L
•
sarebbe utile poter esprimere le interazioni deboli come invarianti sotto rotazioni di isospin
debole SU(2)L, ma ci serve una terza corrente di isospin associata a 3:
jm3
•
•
1
1
1
L m 3 L n L mn L e L m eL
2
2
2
Questa purtroppo non puo’ essere associata a una corrente debole neutra, perché si
accoppia solo a stati left-handed, mentre le correnti deboli neutre hanno una componente
right-handed.
Si risolve il problema introducendo Q=I3+Y/2 , ove ora la corrente e.m. è la somma della terza
componente di isospin debole e della corrente di ipercarica debole. Quest’ultima si accoppia
sia ai doppietti left che ai singoletti right-handed.
em
jm
•
ve
L
e L
1
e R m eR e L m eL jm jmY
2
3
Con Y, si crea un
link fra corrente em
e correnti deboli!
Y è il generatore di un gruppo U(1)Y. La unificazione delle interazioni e.m. e deboli porta a un
gruppo di simmetria SU(2)L x U(1)Y .
jmY 2e R m eR L m L
La corrente di ipercarica si scrive
La lagrangiana del Modello Standard
Il passo finale per scrivere una lagrangiana delle interazioni elettrodeboli con tre
bosoni vettori massivi e un fotone a massa nulla consiste nel considerare il
gruppo SU(2)LxU(1)Y e richiedere l’invarianza di gauge locale indipendentemente
ai due sottogruppi.
Per campi fermionici L si scrive allora
L L m [i m gI Wm
g'
g'
YBm ] L R m [i m YBm ] R ...
2
2
In questa formulazione tutti i campi hanno ancora massa nulla. Termini di massa
per i fermioni rompono anch’essi l’invarianza di gauge di SU(2)L.
Aggiungendo a L i termini relativi a un doppietto di scalari complessi in forma di
doppietto di isospin debole con ipercarica Y=+1,
L (Dmf )† (Dmf ) m 2f †f l (f †f )2
con la derivata covariante
f
1 f1 if2
f ( 0)
(f if )
f
2 3
4
Dm [i m gI Wm ( g ' / 2)YBm ]
0
1
f ( x)
2 v H ( x)
troviamo che la lagrangiana dei campi bosonici contiene ora i termini
e scegliendo il vuoto e la sua espansione come al solito,
(
)
1
g 2v 2
v2
1 2
2 2
3
2
2
2
L [ ( m H ) lv H ]
[(Wm ) (Wm ) ] ( gWm g ' Bm )( gW 3m g ' B m ) ...
2
8
8
I campi W3 e B sono mescolati dalla scelta della gauge unitaria. Possiamo
3
disaccoppiarli con la combinazione lineare
A B cos q W sin q
m
m
W
m
W
Z m Bm sin qW Wm cos qW
dove abbiamo anche definito tan(qW )=g’/g. Con questa sostituzione si trova
(sempre trascurando i termini di interazione):
1
L ( m H ) 2 lv 2 H 2
2
La rottura di
SU(2)xU(1) ha dato
1
g 2v 2
1
1
1
m
1n
n
1m
( mWn n Wm )( W W )
(Wm ) 2
vita precisamente allo
4
8
spettro che volevamo:
1
g 2v 2
2
2
2 2
m
2n
n
2m
( mWn n Wm )( W W )
(Wm )
un bosone scalare
4
8
massivo, due W e una
2
1
v
Z massivi, e un fotone
( m Zn n Z m )( m Z n n Z m ) ( g 2 g '2 ) Z m Z m
4
8
a massa nulla.
1
( m An n Am )( m An n Am ) ...
4
3
All’inizio avevamo 8 gradi di libertà dai bosoni vettori e 4 dal doppietto scalare di higgs. Ora
abbiamo tre bosoni massivi (3x3=9 gradi di libertà), uno massless (2 g.l.) e un bosone
scalare di Higgs.I conti tornano!
Con la scelta Y=1 per il doppietto scalare, esso ha due componenti, una carica (Q=1) a I 3= ½
e una neutra (Q=0) a I3=- ½ perché Q=I3+Y/2. E’ chiaro che solo la componente neutra può
assumere un v.e.v. non nullo – le fluttuazioni del vuoto non generano carica!
Relazioni fra gli accoppiamenti
Am Bm cos qW Wm sin qW
3
Dalle equazioni del mescolamento
Z m Bm sin qW Wm cos qW
3
Wm Am sin qW Z m cos qW
3
che invertite danno
Bm Am cos qW Z m sin qW
si ottiene l’interazione di corrente neutra come
Y
Y
j
j
g
'
m
m
i ( gjm3W m 3 jmY Bm ) i ( g sin qW jm3 g ' cos qW
) Am i ( g cos qW jm3 g ' sin qW
)Z m
2
2
2
Scritta così, si identifica subito l’interazione elettromagnetica, che ha
accoppiamento e, per cui
g sin qW g ' cos qW e
Inoltre, usando la relazione fra correnti
si trova che
jmY 2 jmem 2 jm3
Y
j
g
i ( g cosq j g ' sin q
) Z i
( j sin q j ) Z
2
cosq
m
3
W
m
W
3
m
m
W
2
em
W
m
Considerazioni aggiuntive
•
Possiamo trovare una simmetria residua del vuoto, descritta da un sottogruppo del gruppo
SU(2) LxU(1)Y ? In tal caso il bosone di gauge associato rimane a m=0, come sempre.
In effetti se applichiamo Q allo stato di vuoto troviamo Qf0=(I3+Y/2) f0=0 per cui il vuoto che
abbiamo scelto è effettivamente invariante per una U(1) locale generata da Q:
f0 f '0 eia( x )Qf0 f0
•
Dei quattro generatori I e Y, solo la combinazione Q lascia il vuoto invariante. Il fatto che il
fotone rimanga a massa nulla non è una previsione del modello, ma è implicita nella scelta di
uno stato di vuoto a carica nulla.
•
Usando la massa MW= ½ gv, e il valore misurato della costante di Fermi e della costante di
struttura fine, troviamo:
2
g
G
8mW2
2
, mW
1
vg v ( 2G) -1/2 246GeV
2
a
g sin qW e , a e / 4 mW
2G
mW 80GeV , mZ mW / cos qW 90GeV
1/2
2
•
•
1
sin qW
La massa del bosone di Higgs dipende dal parametro lambda, e non è prevista dal modello.
Vedremo che v è curiosamente vicino a 2½ Mtop più avanti…
La massa dei fermioni
La lagrangiana dei campi di Dirac
L L m [i m gI Wm
g'
g'
YBm ] L R m [i m YBm ] R ...
2
2
non ammette termini di massa se si vuole mantenere l’invarianza di gauge.
Per campi di Dirac i termini di massa sono scrivibili come
mescola doppietti
5
5
1
1
e singoletti
m m [ (1 ) (1 )] m( )
e
e
e
2
2
e
R
L
L
R
I
Se ricordiamo le assegnazioni di isospin e ipercarica debole:
vediamo che il doppietto scalare scelto per descrivere
il campo di Higgs ha proprio i valori “giusti” per
H(I= ½,Y=1)
accoppiare fermioni left e right:
eR(I=0,Y=-2)
(
)
Y
n e 1/ 2 1/ 2 1
eL 1 / 2 1 / 2
1
eR
2
0
0
eL(I= ½,Y=-1)
Possiamo allora aggiungere alla lagrangiana il termine gauge-invariante
f
n
g e [(n e , e) L 0 eR e R f , f 0 e ]
e L
f
I3
Scegliendo il vuoto e le sue fluttuazioni come al solito, la lagrangiana viene a
contenere termini del tipo
ge
ge
v(eL eR eR eL )
(eL eR eR eL )h
2
2
ove è facile identificare con la massa dell’elettrone il termine
gev
me
me
Lm me ee
eeh
v
2
In L notiamo anche il termine di accoppiamento di H al campo fermionico: esso
è proporzionale alla massa del fermione.
Questo fatto è importante per capire la fenomenologia del bosone di Higgs (lo
vedremo più avanti).
Va notato che il meccanismo di Higgs, che ci è servito a dotare di massa i
bosoni vettori W e Z – ottenendo una teoria rinormalizzabile e coerente – ci
“regala” automaticamente termini di massa anche per i fermioni. Assieme a
questi abbiamo dovuto comprare anche i termini di accoppiamento, che infatti
sono proporzionali a m (m=0 zero accoppiamento)
Tuttavia, i valori delle masse sono arbitrari, e rimangono parametri della teoria.
Masse e accoppiamenti
• Quanto visto sopra per i leptoni carichi si può estendere ai quarks e
le masse di questi dipendono anch’esse dal valore di v e da costanti
incognite g.
• In termini del v.e.v. del campo di Higgs, sviluppando il termine
quadratico negli spinori le masse dei fermioni si scrivono
mf = 2-½ gfv.
• I valori degli “accoppiamenti di Yukawa” gf dell’Higgs ai fermioni
coprono un vasto range di valori:
g u 2 105
g c 9 103
gt
g d 4 105
g s 8 104
g b 3 102
g e 3 106
g m 6 104
g 1102
1
• Il Modello Standard non solo non predice il valore dei parametri g,
ma non ne spiega l’ampio range.
• Inoltre, la quasi esatta coincidenza di gt con 1 è un’osservazione di
grande interesse…
Esercizio per casa n°4
Partendo dalla parte di interazione nel termine cinetico del campo scalare espresso
per mezzo della derivata covariante SU(2)xU(1):
Dm [i m gI Wm ( g ' / 2)YBm ]
sostituire il campo scalare nell’intorno del vuoto ,
0
1
f ( x)
2 v H ( x)
(
)
arrivando ad esprimere i termini di massa e di interazione per mezzo degli stati
ruotati relativi ai bosoni fisici W+,W-,Z, e ottenere i termini di massa e accoppiamenti
del W,Z, e fotone. Commentare sulle intensità relative e la presenza o assenza di
termini relativi agli accoppiamenti fra queste particelle, e le implicazioni.
Ricordando che le larghezze sono proporzionali al quadrato degli accoppiamenti al
vertice, usare i valori ottenuti per prevedere il rapporto fra le larghezze di
decadimento
( H WW )
( H ZZ )
(Hint: il termine da sviluppare è
usando anche:
1 1
2
Wm 2 (Wm iWm )
W 1 (W 1 iW 2 )
m
m 2 m
g'
1
0
( g W m Bm )
2
2
2 v H ( x)
e le relazioni fra A,Z e B,W3)
2
Una rivisitazione delle divergenze
• Il meccanismo di Higgs è un metodo elegante per introdurre bosoni
massivi nella teoria, ma non sarebbe obbligatorio se non fosse per
la rinormalizzabilità della teoria
• Abbiamo già notato come i processi di scattering di neutrino su
elettrone siano divergenti se non si include lo scambio di un bosone
massivo W
• L’introduzione dei W a sua volta comporta problemi, in quanto si
dimostra che lo scattering neutrino-W (un processo praticamente
impossibile da generare, ma teoricamente lecito) diverge. Serve un
altro diagramma con scambio di Z per rendere la somma
convergente!
• La soluzione non è unica, ma l’arrangiamento dei bosoni deboli in
una struttura gruppale SU(2) è elegante e economica
• Lo scattering WWWW mostra come il bosone di Higgs entra
direttamente in gioco rendendo convergente il processo. Senza un
bosone scalare H accoppiato ai W non ci sarebbe rinormalizzabilità
della teoria GSW!
QCD nel Modello Standard
Finora abbiamo ignorato le interazioni forti. Esse possono essere introdotte in
modo diretto secondo lo schema della QED, con alcune importanti differenze.
La QCD è basata su una simmetria esatta, SU(3) di colore, che governa le
traformazioni della fase
ig L ( x )Ta
dei campi di colore dei quarks: q ( x) 'q ( x) e s a
q ( x)
I generatori di SU(3) non commutano tra loro,
e questo porta a un’autointerazione dei gluoni,
come per i bosoni vettori deboli:
[Ta , Tb ] if abcTc
Come per la QED, se si parte da
una lagrangiana per quarks
q ( x) q ' ( x) [1 ig s L a ( x)Ta ] q ( x)
colorati e liberi e si impone
Gma ( x) Gma ( x) m La ( x) g s f abcLb ( x)Gmc
invarianza SU(3) locale, si è
forzati a introdurre una covarianza
a
(
D
)
ig
(
T
)
G
m jk
jk m
s
a jk m
della derivata, con otto campi
vettoriali G (corrispondenti
j
1 a mn
j m
k
j
2
L
i
(
D
)
m
Gmn Ga
agli N -1=8 generatori) che
q
m jk q
q
q q
4
q
q
trasformano in modo covariante,
a
e i relativi termini cinetici:
Gmn
m Gn n Gm g s f abcGmb Gnc
•
•
•
La lagrangiana ora vista descrive quarks colorati e gluoni. Otto gluoni sono
necessari a compensare le variazioni arbitrarie nelle fasi La(x) dei tre campi
di colore dei quarks in ogni punto dello spaziotempo
La SU(3) di colore è una simmetria esatta della natura: i gluoni hanno massa
nulla come il fotone
I gluoni hanno autointerazioni, a causa della natura non abeliana di SU(3)
che ha introdotto nella lagrangiana di QCD i termini misti attraverso le
espressioni
Gma ( x) Gma ( x) m La ( x) g s f abcLb ( x)Gmc
a
Gmn
m Gn n Gm g s f abcGmb Gnc
•
La costante gs determina l’intensità delle interazioni forti e copre il ruolo di
“carica” del campo di colore. Si noti però come essa è sempre associata alle
costanti di struttura di SU(3): questo implica diversa intensità per i diversi
accoppiamenti qg e gg.
•
Infine, la natura non abeliana del gruppo SU(3) ha un effetto sulla
dipendenza dal quadrimomento trasferito della costante di accoppiamento
forte as=gs2/4. Studieremo questo effetto nel seguito.
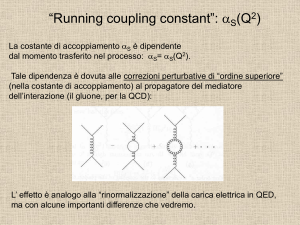
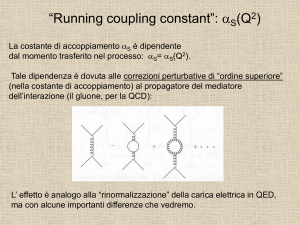
“Running coupling constant”: aS(Q2)
La costante di accoppiamento aS è dipendente
dal momento trasferito nel processo: aS= aS(Q2).
Tale dipendenza è dovuta alle correzioni perturbative di “ordine superiore”
(nella costante di accoppiamento) al propagatore del mediatore dell’
interazione (il gluone, per la QCD):
L’ effetto e’ analogo alla “rinormalizzazione” della carica elettrica in QED,
ma con alcune importanti differenze che vedremo.
Rinormalizzazione della carica elettrica
in QED: aQED(Q2)
In QED, l’ampiezza di scattering, ad esempio, e-e- e-e- , completa a
tutti gli ordini perturbativi e’ data dai diagrammi:
km
em
en
q
p
ea
e
kn
~ e2a
~ e4a2
~ e6a3
Il propagatore nell’ elemento di matrice di transizione viene modificato;
limitandoci al 2o termine in a2:
ig mn
q
2
ig mn
q2
ig ma
ig n
2 a 2
q
q
dove il “loop fermionico” nel propagatore e’ calcolabile integrando su tutti
i possibili 4-impulsi p del fermione
L’integrale è
a
[eu( p) a u( p q)] [eu( p q) u( p)]
d p
4
(2 )
p 2 m2
( p q) 2 m 2
1
4
e si ottiene
a iga q 2(q 2 )
(q 2 )
con:
a0 L
ln 2
3 Q
(a0=e2/4)
L’integrale diverge per |p| (“divergenza ultravioletta”) e viene controllato
da un parametro di cut-off L, che verrà riassorbito, come vedremo, nella
ridefinizione (“rinormalizzazione”) della carica elettrica.
In definitiva, si ha la seguente modifica nel propagatore introdotta dal 2o
termine perturbativo:
ig
ig
mn
q
2
mn
q
2
(1 (q ))
2
e l’ ampiezza di transizione è esprimibile in termini dell’ ampiezza A0(q2)
calcolata dal diagramma ‘lowest order’ (anche detto “tree-level”)
(
~
A1 (q ) a 0 A0 (q ) 1 a 0(q 2 )
2
2
)
dove per comodità
si e’ introdotto:
(q 2 ) 1 L
~ 2
(q )
ln 2
a0
3 Q
Inserendo i contributi negli ordini successivi (diagrammi a più loops), si
ottiene la serie geometrica:
a 0 A0 (q 2 )
~ 2
2
2
2~2
2
A1 (q ) a 0 A0 (q ) 1 a 0(q ) a 0 (q ) ....
~
1 a 0 (q 2 )
(
)
a (Q 2 ) A0 (q 2 )
L’ ampiezza completa a tutti gli ordini perturbativi è esprimibile
tramite l’ ampiezza al primo ordine in a , moltiplicata per la
costante di accoppiamento “rinormalizzata”:
a (Q 2 )
a0
a 0 L2
1
ln 2
3 Q
ossia:
1
1
1 L2
ln 2
2
a (Q ) a 0 3 Q
(1)
Rinormalizzazione in QED: aQED(Q2)
Va notato inoltre che a priori la ridefinizione della carica elettrica è
affetta anche dai contributi “esterni” al propagatore fotonico:
Tuttavia si dimostra, come conseguenza della invarianza di gauge della
teoria, che i contributi (b) + (c) si cancellano col contributo (a) (identità di
Ward in QED; estesa alle teorie di gruppo non abeliane (e.g. la QCD) da
Slavnov-Taylor)
L’ invarianza di gauge di una teoria di campo è essenziale per garantirne
la rinormalizzabilità, ossia la possibilità di riassorbire le divergenze
ultraviolette in un’unica ridefinizione della costante di accoppiamento.
Rinormalizzazione in QED: aQED(Q2)
Negli esperimenti, ciò che si misura è a(Q2) ad una certa scala di
momento trasferito (ad esempio, nello scattering Thomson e-e- e-eo nell’ esperimento che misura il Lamb-shift nella struttura iperfina
dell’atomo di idrogeno : a(Q2 =m2 1eV)=1/137 ).
Queste misure vanno correlate con le misure a scale diverse (ad esempio
Q2 = MZ2 = (91 GeV)2 ); dalla (1) si ottiene
1
1
1 L2 1 L2
1 Q2
ln 2
ln 2
ln 2
2
2
a (Q ) a ( m ) 3 Q 3 m
3 m
(2)
La relazione tra i due valori è dunque esattamente predetta dalla teoria ed
è indipendente dalla divergenza ultravioletta (il valore di cut-off L nell’ integrale
dei loop fermionici interni al propagatore del fotone) che è riassorbita nella
costante di accoppiamento rinormalizzata. Invertendo la precedente si ha
a (m 2 )
a (Q )
a (m 2 ) Q 2
1
ln 2
3
m
2
Rinormalizzazione in QED: aQED(Q2)
La “costante” di accoppiamento e’quindi una “running coupling constant”;
In QED, essa cresce logaritmicamente con l’ impulso trasferito.
[ Qualitativamente, la cosa può essere spiegata dalla “polarizzazione del
vuoto”: le coppie virtuali e+e- che si formano agiscono come i dipoli di un
dielettrico, schermando la carica elettrica “nuda” . Quanto più ci si
avvicina ad essa, aumentando il momento trasferito nello scattering,
tanto maggiore e’ la carica elettrica ‘vista’ nell’ interazione.]
A Q2=MZ2104 GeV2 :
ee+
e-
ea (M Z
2
1
)
132
1
1
1 Q2
1 104
ln 2 137
ln 18 132
2
2
a (Q ) a ( m ) 3 m
3 10
a
a ( M Z2 ) a (Q 2 0)
7%
a
a
QCD: as(Q2)
In QCD il meccanismo e’ analogo, ma con l’ importante differenza che
i gluoni sono portatori di carica di colore:
non esiste il
corrispettivo in QED
Risulta che il loop gluonico contribuisce per un fattore (11/4)ln(Q2/L2) e
per ognuno degli nf quarks che alla scala di Q2 considerata possono essere
creati (mf2< Q2/2) vi e’ un fattore –(1/6)ln(Q2/L2).
In definitiva per la costante di accoppiamento forte si ha:
(3)
a S (m 2 )
a S (Q )
2
1 a S (m )
2
(33 2n f )
12
Q
ln 2
m
2
a S (m 2 )
Q2
1 0.61 a S ( m ) ln 2
m
2
dove si e’ posto nf=5 (ci sono 5 flavours di quark: q = u,d,s,c,b ,
se si considerano le scale m2,Q2>mb225 GeV2)
QCD: as(Q2)
La “costante” aS decresce col momento trasferito (libertà asintotica”),
e varia molto più rapidamente di aQED.
Dallo studio dello spettro degli stati legati del charmonio (stati legati cc ):
aS(mc2 (3GeV)2) 0.25, e propagando alla Z:
Q2
104
1
1
1
8.2
0.61 ln 2
0.61ln
2
2
a S (Q ) a S ( m )
m 0.25
10
[ in realtà si dovrebbe calcolare una doppia propagazione: a(mc2)a(mb2) con b0(nf=4)=0.66,
e a(mb2) a(mZ2) con b0=0.61; la differenza è piccola ]
a S (M Z 2 ) 0.12
a s
as
a s ( M Z2 ) a s (10GeV 2 )
50%
as
Tale predizione è verificata molto bene
sperimentalmente (dalle misure di aS(MZ2)
ottenute, ad esempio, dalla forma degli
eventi di decadimento adronico della Z:
Z qq ; tale forma dipende dal numero
di gluoni irradiati dai quarks nello stato finale,
che dipende da aS).
as(Q2) e LQCD
La dipendenza (3) di aS(Q2) può essere riformulata introducendo il
parametro dimensionale LQCD :
Q2
Q 2
1
1
1
b0 ln 2 b0
ln 2
2
2
2
a S (Q ) a S ( m )
m
m
b0a S ( m )
(4)
m2
Q 2
b0 ln 2 ln 2
(b0 (33 2n f ) / 12 )
L
m
QCD
dove:
m2
ln 2
L
QCD
1
b a (m 2 )
0 S
Con tale definizione, si trova
e in definitiva
ovvero
ln L2QCD ln m 2
Q2
1
b0 ln 2
2
L
a S (Q )
QCD
Q 2
2
a S (Q ) b0 ln 2
L QCD
1
b0a S ( m 2 )
1
relazione che permette di calcolare aS senza alcun riferimento ad una
scala prefissata m2 (ovviamente LQCD viene determinata dalla misura di
a(m2) ad una certa scala; il ‘best fit’ ai dati dà LQCD= (20515) MeV)