Lunghezza circonferenza e area cerchio – sintesi – gen. 2012
LUNGHEZZA CIRCONFERENZA
Volendo misurare la lunghezza della circonferenza, si potrebbe usare un nastro che,
disteso in piano, ci dia la circonferenza rettificata, misurabile con un righello.
Tale metodo non risulta sempre facilmente applicabile.
C’è quindi bisogno di un metodo o regola che ci permetta di calcolare velocemente
la misura di una circonferenza!
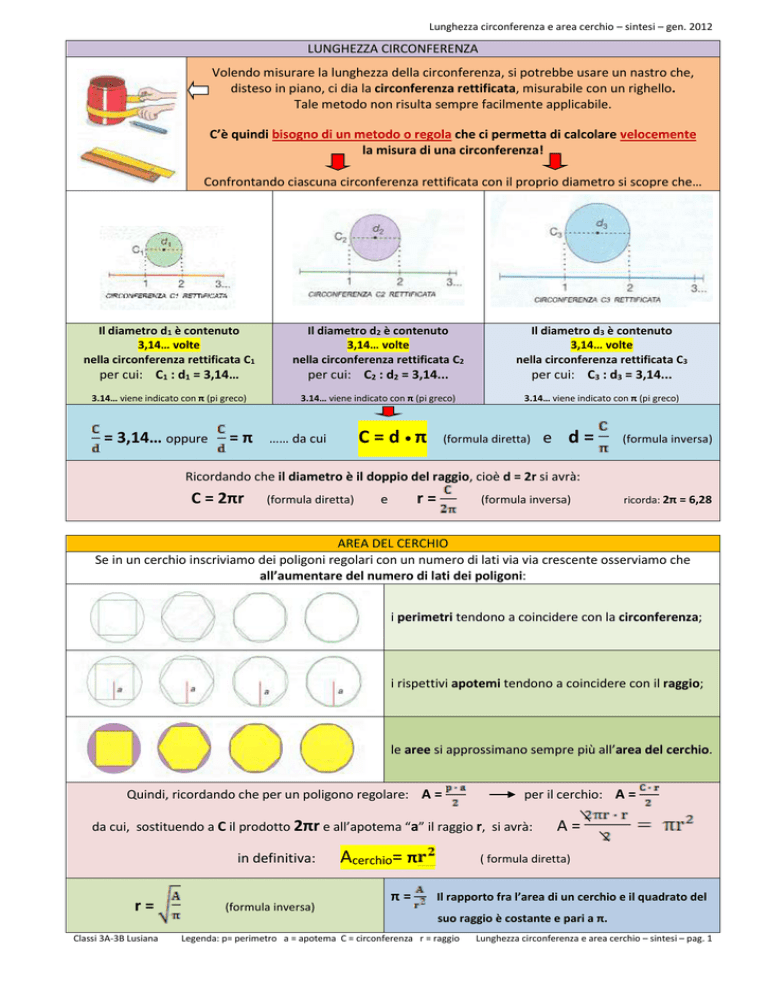
Confrontando ciascuna circonferenza rettificata con il proprio diametro si scopre che…
Il diametro d1 è contenuto
3,14… volte
nella circonferenza rettificata C1
Il diametro d2 è contenuto
3,14… volte
nella circonferenza rettificata C2
Il diametro d3 è contenuto
3,14… volte
nella circonferenza rettificata C3
per cui: C1 : d1 = 3,14…
per cui: C2 : d2 = 3,14...
per cui: C3 : d3 = 3,14...
3.14… viene indicato con π (pi greco)
3.14… viene indicato con π (pi greco)
3.14… viene indicato con π (pi greco)
= 3,14… oppure
=π
C = d •π
…… da cui
(formula diretta)
e d=
(formula inversa)
Ricordando che il diametro è il doppio del raggio, cioè d = 2r si avrà:
C = 2πr
(formula diretta)
r=
e
(formula inversa)
ricorda: 2π = 6,28
AREA DEL CERCHIO
Se in un cerchio inscriviamo dei poligoni regolari con un numero di lati via via crescente osserviamo che
all’aumentare del numero di lati dei poligoni:
i perimetri tendono a coincidere con la circonferenza;
i rispettivi apotemi tendono a coincidere con il raggio;
le aree si approssimano sempre più all’area del cerchio.
Quindi, ricordando che per un poligono regolare: A =
per il cerchio: A =
da cui, sostituendo a C il prodotto 2πr e all’apotema “a” il raggio r, si avrà:
in definitiva:
r=
Classi 3A-3B Lusiana
(formula inversa)
Acerchio= π
π=
A=
( formula diretta)
Il rapporto fra l’area di un cerchio e il quadrato del
suo raggio è costante e pari a π.
Legenda: p= perimetro a = apotema C = circonferenza r = raggio
Lunghezza circonferenza e area cerchio – sintesi – pag. 1
Lunghezza circonferenza e area cerchio – sintesi – gen. 2012
LUNGHEZZA DELL’ARCO
All’angolo al centro di 45° corrisponde l’arco AB.
All’angolo al centro di 90° (45°x 2) corrisponde l’arco AC ( AB x 2).
Quindi, raddoppiando l’angolo al centro (da 45° a 90°), raddoppia anche il
corrispondente l’arco.
Angoli al centro e archi corrispondenti
sono direttamente proporzionali.
Ricordando che ad un angolo al centro di 360° corrisponde tutta la
circonferenza, può essere utilizzata la seguente proporzione:
Circonferenza : arco = 360° : ampiezza arco
da cui può essere ricavata la lunghezza dell’arco
o qualsiasi altro termine incognito a seconda dei casi
AREA DELLA CORONA CIRCOLARE
L’area della corona circolare è data dalla differenza
fra
l’area del cerchio maggiore e l’area del cerchio minore.
Acorona = Acerchio magg. – Acerchio min.
AREA DEL SETTORE CIRCOLARE
Raddoppiando l’ampiezza dell’angolo al centro raddoppia l’area del settore
circolare corrispondente.
Angoli al centro e settori circolari corrispondenti
sono direttamente proporzionali.
Osservando che all’angolo al centro di 360° corrisponde l’area di tutto il
cerchio, può essere utilizzata la seguente proporzione:
Acerchio : A settore circolare = 360° : ampiezza settore
da cui può essere ricavata l’area del settore circolare
o qualsiasi altro termine incognito a seconda dei casi
AREA DEL SEGMENTO CIRCOLARE
Disegnando una qualsiasi corda, si ottengono 2 segmenti circolari,
solitamente uno più grande dell’altro.
Se la corda è un diametro, i 2 segmenti circolari sono congruenti
e vengono detti semicerchi.
L’area del segmento circolare minore è data dalla differenza fra l’area del
settore circolare che insiste sullo stesso arco AB e l’area del triangolo AOB.
ASegmento circ. = A Settore circ. – A Triangolo AOB
L’area del segmento circolare maggiore è data dalla somma dell’area del
settore circolare corrispondente e dell’area del triangolo AOB.
ASegmento circ. = A Settore circ. + A Triangolo AOB
Classi 3A-3B Lusiana
Lunghezza circonferenza e area cerchio – sintesi – pag. 2












