8. Differenziali

Vdd
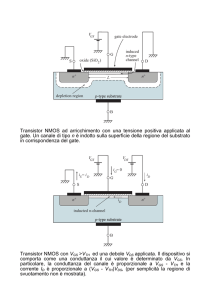
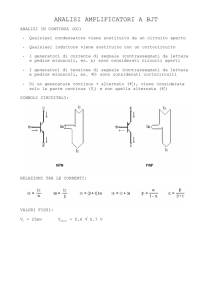
Specchio cascode low-voltage
 Per limitare la caduta di tensione sullo
I1
specchio, ovvero eliminare il
compromesso tra accuratezza e
output swing, abbiamo studiato la rete
di polarizzazione del circuito cascode
illustrata in figura.
 Abbiamo anche stabilito che M1 e M2
funzionano in saturazione se
l’overdrive su M2 è inferiore ad una
soglia
 Rimane da introdurre un’ulteriore ramo
di polarizzazione per la generazione
della tensione Vb
b
M2
NMOSEN W,L
M1
NMOSEN W,L
Caratteristica di trasferimento
 La caratteristica di
trasferimento, confrontata con
quella di uno specchio
cascode semplice, mostra
l’assenza della zona in cui
uno solo dei due mosfet era
in zona di triodo.
 Infatti, essendo polarizzati
alla Vds minima, i dispositivi
entrano simultaneamente in
zona di triodo e rendono così
minima la spesa in termini di
caduta di tensione sullo
specchio
 La tensione Vb, che deve
garantire gli overdrive dei mosfet
di uscita ed anche la soglia del
mosfet cascode, la si genera con
un ulteriore ramo di
autopolarizzazione
Vdd
Generazione di Vb
I1
M3
NMOSEN W,L
 Sul mosfet M1 la tensione
VDS=VGS
M2
NMOSEN W,L
 Sul mosfet M2 la tensione
VDS<VGS dal momento che va
tenuta in conto anche la caduta su
M3
M1
NMOSEN W,L
(continua)
M3 in maniera che la sua
VGS=VDS sia circa pari a VT
(come?)
 In questo modo M2 è
polarizzato al bordo della
zona di pinch-off e si ha:
Vdd
 In particolare si dimensiona
I1
M3
NMOSEN W,L
Vb = Vgs2 - VTH + Vgs1 =
Vgs2 - VTH + Vgs1 - VTH + VTH
Vov 2
Vov1
Vb
M2
NMOSEN W,L
M1
NMOSEN W,L
Il circuito complessivo
Lezione IX
Amplificatori differenziali
Premessa
 Nel corso di Elettronica analogica avete appreso le modalità di funzionamento
ad ampi e piccoli segnali dell’amplificatore differenziale realizzato con mosfet.
 Ne conoscete le versioni a carico resistivo e carico attivo (specchio di corrente)
 Avete anche usato il circuito differenziale come elemento fondamentale per la
realizzazione di un amplificatore operazionale CMOS
 Con queste basi, svilupperemo l’analisi di questo circuito con una maggiore
attenzione riguardo ai criteri di progettazione e dimensionamento dei mosfet
Amplificatore Differenziale con carico
resistivo
Carico resistivo
Analisi ad ampi segnali
La tensione differenziale di ingresso è data dalla differenza tra le tensioni gate-source di
M1 e M2
Vin1  Vin 2  Vgs  Vgs 2
Analisi ad ampi segnali
Se M1 e M2 sono polarizzati in pinch-off possiamo scrivere le note equazioni delle
correnti e risolverle per Vgs1 e Vgs2
2
1
W 
I D1  nCox   Vgs1  VTH   Vgs1 
2
 L 1
I D2
2
1
W 
 nCox   Vgs 2  VTH   Vgs 2 
2
 L 2
2 I D1
 VTH
W 
nCox  
 L 1
2I D 2
 VTH
W 
nCox  
 L 2
…
Sottraendo entrambi I membri, possiamo quindi valutare la tensione differenziale di
ingresso in funzione della corrente di drain di M1 e M2
Vin1  Vin 2 
2 I D1
2I D2

W 
W 
nCox  
nCox  
 L 1
 L 2
…
Il nostro scopo è di valutare le correnti in funzione della tensione differenziale. Eleviamo
quindi al quadrato entrambi I membri
Vin1  Vin 2 
2




2
I
2
I
D
1
D2




W 
W  
n Cox   
  n Cox  L 
 1
 L 2 

2
(continua)
Se M1 e M2 sono uguali
e sviluppiamo il secondo membro

2 I D1  I D 2  I D1I D 2
2 I D1
2I D 2
I D1I D 2
2



W 
 W  nCox  W   W 
W 
nCox   nCox  
nCox  
  
 L 1
 L 2
 L 1  L 2
L
Ricordando che
I SS  I D1  I D 2

1
2
W 
nCox   Vin1  Vin 2   2 I SS  I D1I D 2
2
L


In definitiva
Possiamo quindi scrivere le due equazioni che legano le correnti di drain alla tensione
differenziale di ingresso e che, risolte, forniscono la caratteristica di trasferimento per
ampi segnali del nostro amplificatore differenziale




1
2
W 
nCox    Vin   2 I SS  I D1  I SS  I D1 
2
L
1
2
W 
nCox    Vin   2 I SS  I D 2  I SS  I D 2 
2
L
Caratteristica di trasferimento
Zona di funzionamento lineare
55uA
I(M2)
I(M1)
50uA
45uA
40uA
35uA
30uA
25uA
20uA
15uA
10uA
5uA
0uA
-500mV
-300mV
-100mV
100mV
300mV
500mV
(continua)
 E’ anche utile vedere a quale tensione Vgs si mettono a lavorare
M1 e M2 se ΔVin=0
2
I SS
I SS
1
W 
nCox   Vgs  VTH 1,2 
 Vgs  VTH  
2
2
W 
L
nCox  
L
I SS
Vgs 
 VTH
W 
nCox  
L
 Ancora ricordiamo che l’amplificatore differenziale con carico
resistivo guadagna come un equivalente stadio a source comune
Risposta al modo comune
 Il circuito in figura rappresenta
un AD in configurazione di
modo comune
 La polarizzazione viene
effettuata attraverso un
generatore di corrente di cui, a
piccolo segnale, consideriamo
la sola resistenza differenziale
di uscita
 Vogliamo determinare il
guadagno di questo stadio
Mezzo circuito equivalente
 La simmetria del circuito ci
consente di analizzarne solo la
metà
 La corrente di polarizzazione si
dimezza mentre la resistenza
di uscita del generatore di
corrente deve raddoppiare
 Il guadagno di questo stadio è
dato da:
Av  
RD
1
W
2  n Cox 
L
 I SS

 2
 2 RSS
Esempio
 Supponiamo che Rss sia scelto
in maniera da garantire una
corrente di polarizzazione dello
specchio pari ad 1 mA.
 Se (W/L)=20/0.5,
μnCox=50uA/V2, VTH=0.6V e
VDD=3V
 Qual è il minimo valore di
modo comune che garantisce
una caduta su Rss pari a
0.5V?
 Determinare Rd che impone
un guadagno differenziale
pari a 5
 Cosa succede al circuito se il
valore di modo comune
aumenta di 50 mV?
(a)
 Dal momento che su Rss devono cadere 0.5V il valore di Rss è
pari a 1mA/0.5V=500Ω
 Per avere su Rss una caduta di 0.5V si deve avere che:
I SS
1
2
W 
nCox   VCM  0.5  VTH  
 0.5mA
2
2
L
I SS
1
2
6
50 10  50 VCM  0.5  0.6  
 0.5mA
2
2
VCM  0.5  0.6 
2
 0.4  VCM  0.63  0.5  0.6  1.73V
(b)
 Il guadagno è dato da:
W
Av   g m RD  2nCox 
L
 I SS
RD 

 2
  2  50 106  50  0.5 103 RD
se Av  5  R  3.16k 
 Il livello di continua sui nodi di uscita è dato da
Vout  Vdd  Rd I d  1.42V
(c)
 Se il valore di modo comune aumenta di 50mV, anche il
valore del potenziale di source dovrà variare di
conseguenza e quindi i dispositivi vedranno ridotta la
loro tensione Vds
 Di conseguenza i due mosfet si avvicinano alla zona di
triodo
Amplificatore asimmetrico
 Le variazioni di modo comune
risultano essere molto dannose
rispetto all’amplificazione di modo
differenziale se, come è nella
realtà, i due rami del differenziale
non sono proprio uguali
 Supponiamo ad esempio che
R1=Rd e R2=Rd+ΔRd e che il
differenziale sia polarizzato con
un generatore la cui impedenza di
uscita è proprio Rss
(continua)
 Si avrà:
Vout1  
RD
1
 RSS
2 gm
Vout1  Vout 2
VCM ;


RD
RD  RD
 

1
 1 R
 RSS
SS
 2g
2 gm
 m
Vout 2
RD  RD

VCM
1
 RSS
2 gm


2 g m RD
 VCM  
VCM
1  2 g m RSS



Ovvero nasce una componente di modo differenziale in
risposta ad un segnale dei modo comune!!
(continua)
 Anche differenze tra i mosfet, che si manifestano come
differenze di gm, portano a segnali differenziali dovuti a
componenti di modo comune.
 E’ possibile provare che:
Vout1  Vout 2
gm RD

 ACM  DM
VCM
1  2  gm1  gm 2  RSS
Guadagno di conversione CM-DM
Definizione
 Si definisce rapporto di reiezione di modo comune, o anche
CMRR, il rapporto tra l’amplificazione di modo differenziale e
l’amplificazione di conversione da modo comune a modo
differenziale dovuta alle asimmetrie del circuito
CMRR 
ADM
ACM  DM