file

Omotetie e similitudini
Definizione
Dati un punto O del piano α e un numero reale k ≠ 0, si dice omotetia di centro O e
rapporto k la trasformazione del piano in sé che associa ad ogni punto P di α il
punto P’ di α tale che:
 O, P, P’ siano allineati
 OP’ ≅ |k| OP
 P’ appartenga alla semiretta OP se k > 0 (omotetia diretta)
P’ appartenga alla semiretta opposta ad OP se k < 0 (omotetia inversa)
L’omotetia diretta viene indicata con il simbolo ωo,k, quella inversa con ωo,-k.
OP
 1 quindi P’ coincide con P.
OP
 Se k = 1 l’omotetia coincide con l’identità, infatti
OP
 Se k = -1 l’omotetia coincide con la simmetria centrale, infatti
OP
OP’ e OP sono opposti.
 1 e i segmenti
1
Omotetie e similitudini
Esempio
ESEMPIO
Dato il triangolo ABC costruiamo A’B’C’ = ωo,-½ (ABC)
Il rapporto di omotetia è negativo (-½), quindi i punti omotetici A’, B’, C’ si trovano sulle
semirette opposte a OA, OB e OC.
Troviamo i corrispondenti dei vertici:
OA’ = ½ OA
OB’ = ½ OB
OC’ = ½ OC
2
Omotetie e similitudini
Proprietà
L’omotetia gode delle seguenti proprietà:
• trasforma un segmento AB in un segmento A’B’
ad esso parallelo tale che A’B’ ≅ |k| AB
k>0
k<0
• trasforma una retta r in una retta r’ ad essa parallela
• trasforma una semiretta in una semiretta parallela
concorde se k > 0, parallela discorde se k < 0
k>0
k<0
• trasforma un angolo in un angolo ad esso
congruente con i lati paralleli e concordi se k > 0,
paralleli e discordi se k < 0.
3
Omotetie e similitudini
Proprietà
CONSEGUENZE:
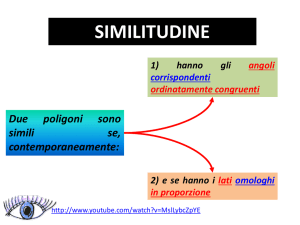
 se due poligoni si corrispondono in una omotetia, allora hanno i lati omologhi
paralleli e di rapporto |k| e gli angoli omologhi congruenti.
Inoltre:
• se |k| > 1 si ottiene un ingrandimento della figura
• se |k| < 1 si ottiene una riduzione
• se k ≠ 1 il solo punto unito della trasformazione è il centro O
• ogni retta passante per il centro è unita ma non è una retta di punti uniti
• il rapporto tra i perimetri di due poligoni omotetici è |k|
• il rapporto fra le aree di due poligoni omotetici è k2
4
Omotetie e similitudini
Prodotto di omotetie
Componendo due omotetie entrambe di centro O e rapporti rispettivamente h e k
si ottiene ancora una omotetia di centro O e rapporto hk.
Se le due omotetie hanno centri diversi P e Q, allora:
• se hk = 1 si ottiene una traslazione
5
Omotetie e similitudini
Prodotto di omotetie
• se hk = -1 si ottiene una simmetria centrale il cui centro è allineato con P e Q
• se |hk| ≠ 1 si ottiene una omotetia di rapporto hk il cui centro è allineato con P e Q
6
Omotetie e similitudini
Prodotto di omotetie
ESEMPIO
Dato un triangolo ABC e le omotetie ωP,2 e ωQ,⅓, costruiamo A’B’C’ = ωP,2 (ABC) e successivamente
A’’B’’C’’ = ωQ,⅓ (A’B’C’).
I triangoli A’’B’’C’’ e ABC si corrispondono nell’omotetia di rapporto k = 2 · ⅓ = ⅔ e di centro O,
intersezione di AA’’ con BB’’.
I punti P, O e Q sono allineati e CC” passa per O.
7
Omotetie e similitudini
Definizione
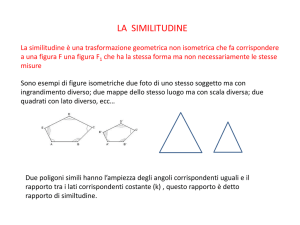
Si chiama similitudine la trasformazione geometrica che si ottiene dal prodotto di una omotetia con una
isometria, in qualunque ordine queste trasformazioni vengano applicate.
Per indicare che due figure G e G’ sono simili si scrive G ~ G’
ESEMPIO
Applichiamo alla figura F una omotetia di centro O e rapporto k e successivamente una simmetria di
asse r.
F ~ F’’
8
Omotetie e similitudini
Proprietà
Per la similitudine valgono tutte quelle proprietà che valgono contemporaneamente per una omotetia e
per una isometria, quindi, in una similitudine:
 il rapporto fra segmenti corrispondenti è costante ed è uguale al valore assoluto del rapporto di omotetia;
esso prende il nome di rapporto di similitudine e lo indicheremo con k
 angoli che si corrispondono sono congruenti
 la figura simile a una retta è una retta
 se due rette sono parallele anche le loro corrispondenti lo sono e se due rette sono incidenti anche le
loro corrispondenti sono incidenti allo stesso modo.
Inoltre:
 due figure omotetiche sono anche simili (l’isometria in questo caso coincide con l’identità)
 due figure congruenti sono anche simili (l’omotetia ha rapporto k = 1).
9
Omotetie e similitudini
Riconoscere poligoni simili
Se due poligoni hanno:
 i lati ordinatamente proporzionali:
AB
BC CD
AD
=
=
=
A¢B¢ B¢C¢ C¢D¢ A¢D¢
 gli angoli ordinatamente congruenti:
A @ A¢
B @ B¢
C @ C¢
D @ D¢
allora sono simili.
Per i triangoli esistono inoltre tre criteri di similitudine
10
Omotetie e similitudini
I criteri di similitudine
Teorema (I criterio di similitudine). Due triangoli sono simili se hanno due angoli ordinatamente
congruenti.
11
Omotetie e similitudini
I criteri di similitudine
Teorema (II criterio di similitudine). Due triangoli sono simili se hanno due lati proporzionali e l’angolo
fra essi compreso congruente.
12
Omotetie e similitudini
I criteri di similitudine
Teorema (III criterio di similitudine). Due triangoli sono simili se hanno i tre lati proporzionali.
13
Omotetie e similitudini
Criteri di similitudine
ESEMPIO
Da un punto M del lato AB di un triangolo ABC tracciamo la parallela al lato BC
che incontra in N il lato AC; dimostriamo che i triangoli ABC e AMN sono simili.
Hp. MN ║ BC
Th. ABC ~ AMN
Possiamo condurre la dimostrazione in diversi modi:
• possiamo dire che i due triangoli si corrispondono nell’omotetia di centro A e che quindi sono
anche
simili
• possiamo dire che i due triangoli hanno l’angolo di vertice A in comune ed inoltre, per il teorema di
Talete, AM : AB = AN : AC; essi sono quindi simili per il secondo criterio
• possiamo dire che, essendo MN ║ BC, i lati dei due triangoli sono proporzionali (conseguneza del
teorema di Talete) e che essi sono quindi simili per il terzo criterio
• possiamo dire che i due triangoli hanno due angoli ordinatamente congruenti: ANM ≅ ACB e
AMN ≅ ABC perché corrispondenti e che essi sono quindi simili per il primo criterio
14
Omotetie e similitudini
Proprietà dei triangoli simili
Se due triangoli sono simili con rapporto di similitudine uguale a k:
 il rapporto fra altezze, mediane, bisettrici omologhe è uguale a k
CH
CM
CF


k
CH ' C ' M ' C ' F '
 il rapporto tra i perimetri è uguale a k, cioè:
2p
k
2 p'
 il rapporto tra le aree è uguale al quadrato del rapporto di similitudine, cioè:
S
 k2
S'
15
Omotetie e similitudini
Corrispondenza con i teoremi di Euclide
Dalla similitudine dei triangoli ABC, ABH e ACH si deduce che:
• in ogni triangolo rettangolo ciascun cateto è medio proporzionale fra l’ipotenusa e la proiezione
del cateto stesso sull’ipotenusa
• in ogni triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale fra le proiezioni
dei cateti sull’ipotenusa
16
Omotetie e similitudini
Similitudine e circonferenza
Relativamente ad una circonferenza e alle sue corde, secanti e tangenti, valgono le seguenti proprietà:
• se due corde di una circonferenza si intersecano, i segmenti di una corda sono i medi, i segmenti
dell’altra corda sono gli estremi di una proporzione
CP : BP = AP : DP
• se da un punto esterno a una circonferenza si tracciano due secanti, una secante e la sua parte
esterna sono i medi, l’altra secante e la sua parte esterna sono gli estremi di una proporzione
PD : PB = PA : PC
17
Omotetie e similitudini
Similitudine e circonferenza
• se da un punto esterno a una circonferenza si tracciano una secante e una tangente, il segmento di
tangente è medio proporzionale fra l’intera secante e la sua parte esterna
PB : PQ = PQ : PA
18
Omotetie e similitudini
Similitudine e circonferenza
Vale inoltre il teorema di Tolomeo:
Teorema. Se un quadrilatero è inscrittibile in una circonferenza, il rettangolo che ha per dimensioni le
diagonali è equivalente alla somma dei rettangoli che hanno per lati i lati opposti del quadrilatero.
r (AC, BD) r (AB, CD) + r (BC, AD)
E il suo inverso:
Se in un quadrilatero il rettangolo che ha per dimensioni le diagonali è equivalente alla somma dei
rettangoli che hanno per lati i lati opposti, allora il quadrilatero è inscrittibile in una circonferenza.
19