Corso di Elettrotecnica
Allievi aerospaziali
Reti Elettriche – Parte I
Revisione aggiornata al 5 4 2011
(www.elettrotecnica.unina.it)
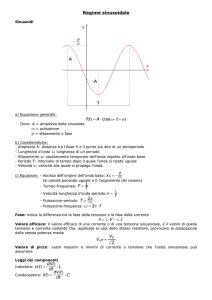
Oggetto del corso
• Studio delle reti elettriche
- reti in regime stazionario
- reti in regime lentamente variabile ed
in particolare sinusoidale
• Elementi di impianti elettrici
- il trasformatore
- elementi di sicurezza elettrica
Supporti didattici
• Giulio Fabricatore: “Elettrotecnica ed
applicazioni” Liguori Editore
• Appunti integrativi su:
- Trasformatore
- Esercizi numerici
• Slides del corso
Tipologia delle reti elettriche
considerate
Reti di bipoli
Definizione preliminare di
bipolo: Oggetto elettrico
facente capo a due
morsetti terminali A e B,
che sono attraversati
dalla corrente i e a cui è
applicata la tensione v. Si
considera il
funzionamento dei singoli
bipoli “a scatola chiusa”,
partendo dalle relazioni
tra v ed i.
Richiami preliminari
Corrente elettrica, tensione
elettrica e forza elettromotrice
La corrente elettrica
(di conduzione)
Δq carica netta che,
nell’intervallo di tempo Δt,
transita nel verso diretto
dalla sez. A alla sez. B
attraverso la sez. S.
q q q q q
i lim t o
q
t
Vettore densità di corrente
(di conduzione)
Il vettore densità di
corrente di conduzione
da A verso B attraverso la
superficie S è definito da:
i G ndS
S
Corrente elettrica in un conduttore
filiforme
Definizione di Ampére.
In 2 conduttori filiformi,
rettilinei, paralleli e
indefiniti posti in aria
circola la corrente di un
A, se tra di essi si
esercita una forza pari a
2·10-7 N per metro di
lunghezza.
Misura della corrente
(amperometro ideale)
L’amperometro ha 2
morsetti,uno + ed uno Misura della corrente da
A verso B.
Misura della corrente da
B verso A.
Diversi tipi di corrente
K
Corrente nei conduttori
metallici, costituita da un
flusso di elettroni
(e=-1.6·10-19 coulomb)
Corrente nei conduttori
elettrolitici costituiti da un
flusso di ioni positivi e
negativi
La corrente nei semiconduttori
Struttura cristallina del
silicio
Conduzione di tipo p
(positiva) costituita da un
flusso di “buchi”
La corrente di spostamento
La corrente di spostamento jS attraverso una
superficie S invariata nel tempo ed immersa in
un mezzo lineare di costante dielettrica ε è data
da:
( K )
jS
ndS
t
S
La quantità ( K ) rappresenta il vettore
t
densità di corrente di spostamento
Un esempio di corrente di
spostamento
v
S
La corrente totale
La somma della corrente di conduzione i e della
corrente di spostamento jS:
itot=i+jS
è detta corrente totale. Il corrispondente vettore densità
è solenoidale:
( K )
[G t ] nd 0
Pertanto la somma delle correnti di conduzione i e di
spostamento jS uscenti dalla (o entranti nella) superficie
chiusa Σ è nulla.
La tensione elettrica
Data una linea ϒ di estremi A e B si dice tensione da A
a B lungo ϒ, la quantità
B
TAB ( ) K tdl
A
che rappresenta il lavoro compiuto dal campo elettrico K
per spostare l’unità di carica positiva da A a B lungo ϒ.
L’unità di misura della tensione è il volt [V]. 1 volt=1
joule/coulomb. (1 coulomb =1 ampére·secondo). Se il
campo elettrico è conservativo la tensione è
%
La tensione elettrica
indipendente da γ. Il
campo elettrico è dotato
di potenziale:
K V
'
TAB TA ' B V ( A) V ( B)
La d.d.p. tra A e B può
essere formalmente
indicata come
V ( A) V ( B) VAB
AB
AB
Misura della tensione elettrica
(voltmetro ideale)
Il voltmetro ha 2
morsetti,uno + ed uno Misura della d.d.p. VAB
Misura della d.d.p. VBA
Forza elettromotrice
Si dice forza elettromotrice (f.e.m.) agente lungo una
linea chiusa orientata γ la quantità scalare algebrica:
e K tdl
Essa è diversa da zero solo se K non è conservativo
sulla linea γ o almeno su di una sua parte e quindi se γ
è immersa in tutto o in parte in una regione dello spazio
R sede di fenomeni fisici di trasformazione d’energia.
L’esempio della pila
(funzionamento a vuoto)
Sia KT la forza totale
agente sull’unità di carica.
e K T tdl
KT Ke Ki
dove K e è il campo
elettrostatico creato dalla
distribuzione di cariche
sugli elettrodi e K i è il
campo di natura
2
1 2
1 da A a B
2 da B ad A
%
L’esempio della pila
(funzionamento a vuoto)
elettrochimica presente
solo all’interno della
soluz. elettrolitica,dove:
KT K e Ki 0
Nell’aria si ha:
K i 0 KT K e
2
e K e tdl K i tdl
e (
0
2
)
e VAB
A
A
B
B
K
i tdl ( 2 ) K e tdl [V ( B ) V ( A)] VAB
F.e.m derivante dall’induzione
elettromagnetica
Solenoidalità del vettore
induzione magnetica B
B ndS 0
S S1 S2
S
B ndS
S1
B n1dS B n 2 dS 0
S2
S
S1
B n1dS B n 2 dS
S2
F.e.m derivante dall’induzione
elettromagnetica
Flusso concatenato con una linea chiusa orientata γ
Per la solenoidalità del vettore induzione magnetica i due integrali
di superficie estesi a S1 e S2 sono indipendenti dalla superficie
purché questa sia orlata da γ.
Dati il vettore induzione magnetica B ed una linea chiusa
orientata γ si definisce pertanto flusso di tale vettore concatenato
con γ la quantità:
B ndS
S
in cui Sγ è una qualsiasi superficie orlata da γ e la normale n
Sγ è orientata in maniera congruente all’orientazione di γ.
a
F.e.m derivante dall’induzione
elettromagnetica
Flusso concatenato con una linea chiusa
orientata γ
Congruenza del verso della normale alla superficie S
rispetto a quello della linea γ
F.e.m derivante dall’induzione
elettromagnetica
Legge di Faraday
Per effetto della variabilità nel tempo dell’induzione
magnetica, nella linea chiusa orientata γ insorge una
f.e.m. data da:
d
e
dt
in cui vale il segno – se il flusso concatenato con γ è
calcolato con la stessa orientazione di γ con cui è
definita la f.e.m e.
Definizione di bipolo
Si definisce bipolo un
oggetto elettrico
racchiuso da una
superficie S, da cui
fuoriescano due
morsetti A e B; S sia
scelta in maniera tale
che: 1) iA=iB; 2) K sia
conservativo su S e
nelle sue immediate
vicinanze; 3) vi sia
assenza di forze di
natura non elettrica. Il
regime di funzionam. è
stazionario o
lentamente variabile
( K )
S [G t ] ndS 0
se
( K )
0
t
G ndS 0
S
iA iB
B
0
t
d
e K dl 0
dt
se
TAB VAB
Esempi di bipoli
A
S
B
Indut tan za
di
vL
dt
Pila ideale
ve
Esempi di bipoli: la capacità
i
A
v
S
B
Convenzioni dei segni in un bipolo
Potenza assorbita da un bipolo
(convenzione dell’utilizzatore)
K dF
dF dq K (idt ) K
B
dL (idt ) K dl vidt
A
pass
dL
vi
dt
Il lavoro dL secondo la
direzione della forza per
spostare la carica dq dal
punto a potenziale più
alto A a B (lavoro
assorbito dal bipolo) è:
B
dL dF dl
A
La potenza corrispond. è
pass=vi: tale espressione
è esatta in regime staz.
ed approssim. in regime
lentamente variab.
Potenza erogata da un bipolo
(convenzione del generatore)
K
dF
Il lavoro dL contro la
direzione della forza
(lavoro erogato dal
bipolo) è:
B
dL dF dl
dF dq K (idt ) K
B
dL (idt ) K dl vidt
A
A
La potenza corrispond.
erogata dal bipolo è:
perog
dL
vi
dt
Potenza erogata da un bipolo
(convenzione dell’utilizzatore)
K dF
Il lavoro dL contro la
direzione della forza
(lavoro erogato dal
bipolo) è:
A
dL dF dl
dF dq K (idt ) K
A
dL (idt ) K dl vidt
B
B
La potenza corrispond.
erogata dal bipolo è:
perog
dL
vi
dt
Potenza assorbita da un bipolo
(convenzione del generatore)
K
dF
Il lavoro dL secondo la
direzione della forza
(lavoro assorbito dal
bipolo) è: A
dL dF dl
dF dq K (idt ) K
A
dL (idt ) K dl vidt
B
B
La potenza corrispond.
erogata dal bipolo è:
pass
dL
vi
dt
Potenza assorbita o erogata da un
bipolo
Convenzione
dell’utilizzatore
Convenzione del
generatore
p assorbita =vi
p erogata =-vi
p erogata =vi
p assorbita =-vi
Misura della potenza
La misura della potenza
assorbita (o erogata) da
un bipolo si fa con il
wattmetro, che presenta
2 coppie di morsetti: una
coppia amperometrica
attraversata da i ed una
voltmetrica, cui è
applicata v. Ciascuna
coppia ha un morsetto +.
I principio di Kirchhoff (Legge di
Kirchhoff delle correnti -LKC)
i4
Per la definizione di
bipolo:
G ndS 0
S
i1 i2 i3 i4 0
i3
i1
In generale:
m
i
k
0
1
m numero lati confluenti
nel nodo
i2
II principio di Kirchhoff (Legge di
Kirchhoff delle tensioni -LKT)
v1
Per la definizione di
bipolo:
K dl 0
K dl
B
C
D
A
A
B
C
v4
v2
D
v1 v2 v3 v4 0
In generale:
m
vk 0
1
m è il numero di lati della
maglia
v3
Reti in regime stazionario
Analisi delle reti
Caratteristica statica di un bipolo
Si dice caratteristica
statica di un bipolo la
relazione:
V=f(I))
che lega la tensione V
applicata ai morsetti A e
B alla corrente I che lo
attraversa in regime
stazionario.
Due bipoli si dicono
equivalenti se hanno la
stessa caratteristica
Dipendenza della caratteristica
dalle convenz. dei segni di V ed I
%
Dipendenza della caratteristica
dalle convenz. dei segni di V ed I
Classificazione dei bipoli: bipoli
lineari e non lineari
Si dice lineare un bipolo la
cui caratteristica è
lineare.
Si dice non lineare nel
caso contrario
Classificazione dei bipoli:bipoli
inerti e bipoli non inerti
Si dice inerte un bipolo la
cui caratteristica la
caratteristica passa per
l’origine degli assi.
Si dice non inerte nel
caso contrario
Classificazione dei bipoli:
bipoli passivi
Si dice passivo un bipolo
per il quale la potenza
assorbita è maggiore o
eguale a zero. Esso
funziona sempre da
utilizzatore.
pass vi
V·I≥0
Classificazione dei bipoli:
bipoli attivi
Si dice attivo un bipolo
non passivo. In alcune
regioni del piano V,I esso
funziona da generatore in
altre da utilizzatore.
V·I>0
V·I≤O
V·I≥0
Convenzione utilizzatore
Una rete elementare
I1
I2
V1
V2
V1 f1 ( I1 )
V2 f 2 ( I 2 )
V1 V2 0
V1 V2 V
I1 I 2 0
I1 I 2 I
f1 ( I ) f 2 ( I ) V
Bipoli lineari ideali
Bipolo Resistenza
V RI
oppure
I GV
1
(G )
R
V RI
oppure
I GV
G
Potenza assorbita dal bipolo
Resistenza
Convenzione utilizzatore
Pass=V∙I=(R∙I)∙I=R∙I2;
Pass= V2/R=G V2.
Convenzione generatore
Pass=-V∙I=-(-R∙I)∙I=R∙I2;
Pass= V2/R=G V2.
Una diversa caratterizzazione
del bipolo resistenza
Vn, Pn
Vn2
R
Pn
10 V, 20 W
R5
500 V, 50 kW
R5
Resistenza reale di un
conduttore
La resistenza di un conduttore cilindrico di sezione S e
lunghezza L è dato da:
R
l
S
dove ρ è la resistività variabile con la temperatura T:
ρ= ρ0(1+αT)
ρ0 resistività a 0 0C
Generatore ideale di tensione
V=E
Generatore ideale di corrente
I=J
Corto circuito ideale
V=0
Aperto ideale
I=0
Serie e parallelo di bipoli
V1
Vn
V2
I1
In
I1 I 2 .....I n I
I2
A
V
B
n
V Vk
1
A
I
I1
V
V1
I2
V2
In
Vn
V1 V2 .....Vn V
n
I Ik
1
B
Resistenze in serie
V
n
V Vk
Vk R k I
1
n
V I Rk Req I
1
V
n
Req Rk
1
Resistenze in parallelo
n
V
Ik
GkV
Rk
I Ik
1
n
I V Gk GeqV
1
V Req I
Req
Req
Req
Se
n
1R
1
k
Req
1
n
G
1
Se n=2
1
1
Geq
1
1
1
R1 R2
R1 R2 R
R
2
R1 R2
R1 R2
k
Generatori ideali di tensione in
serie e in parallelo
n
E E k E eq
1
E=E1=E2
I=I1+I2
Equivalenza di bipoli
V V1 V2
I1
I1 I 2 I
V2
V1
V1 RI
I2
I2 0
V RI
V2 0
Equivalenza di bipoli
V1
V2
V1 V2 V 0
I1 I
I2 0
Equivalenza di bipoli
V=E
I=J
Bipolo di Thévenin
RT
LKT
VR
E VR V 0
VR RT I
Caratteristica statica
V E RT I
E
RT
I cc
I cc E / RT
Bipolo di Norton
IR
LKC
J IR I 0
RN
dove
I R V / RN
J
V
I 0
RN
Caratteristica statica
V RN ( J I )
RN
J
Equivalenza del bipolo di Norton
al bipolo di Thévenin
Norton
Thévenin
E
RN
RT
J
I cc
Il bipolo di Norton è equivalente al bipolo di Thévenin se:
R N RT
J I cc
Generatore reale di tensione
Pila reale sotto carico
Circuito equivalente
Ri
Generatore reale di tensione
Ri
Iu
Vu
A
Ru
Ri I u
E
Vu
Ru
O
Vu E Ri I u
Vu Ru I u
P
Iu
E
Iu
Ru Ri
Ri
B
I cc
Vu E
Ru
Ru Ri
Potenza utile erogata dal
generatore reale di tensione
Pu
Potenza utile
Pu Vu I u Ru I u2
E2
Ru
( Ru Ri ) 2
1
EI cc
4
Il massimo di Pu al
variare di Ru si ha se:
Pu
0
Ru
Ru Ri
1
Ru / Ri
Bilancio delle potenze e
rendimento
LKT
Ri
E Vu Ri I u ( Ru Ri ) I u
Iu
Vu
Ru
EI u Vu I u Ri I u2
Pc
Pu
PJ
Pc ( Ru Ri ) I u2
Pu Ru I u2
Pu
Ru
Pc Ru Ri
Ru / Ri
Caduta di tensione nel
generatore reale di tensione
Caduta di tensione
Ri
Iu
V E Vu Ri I u
Vu
Ri
E
Ru Ri
V %
Ri
V
100
100
E
Ru Ri
Ru
V %
Ru / Ri
Parallelo di generatori reali di
tensione
Ic=0 se
E1=E2
E1 E2
Ic
Ri1 Ri 2
Una particolarizzazione della
LKT
LKT per una generica
maglia a m lati
m
()V
k
0
dove
1
Vk Ek Rk I k
Generico lato k-esimo
Ik
Rk
Ek
Vk
m
()( E
k
Rk I k ) 0
1
m
() E
1
m
k
( ) Rk I k
1
Un esempio
I1
E1
R1
R2
R4
E1 E2 R1 I1 R2 I 2 R3 I 3 R4 I 4
E2
I4
I3
I2
R3
Formule del partitore di tensione
Ripartizione della
tensione V applicata a 2
resistenze in serie
V1 R1 I
V2 R2 I
V
I
R1 R2
V1 V
V2 V
R1
R1 R2
R2
R1 R2
Formule del partitore di corrente
Ripartizione della corrente
I tra due resistenze in
parallelo
V
I1
R1
I2
V
R2
R1 R2
V ( R1 // R2 ) I I
R1 R2
I1 I
R2
R1 R2
I2 I
R1
R1 R2
Trasformazioni triangolo-stella e
stella-triangolo
Equivalenza di tripoli di
resistenze
Condizioni di equivalenza tra
tripoli di resistenze
R AB ( RBC R AC )
J
J ( R A RB )
R AB RBC R AC
Condizioni di equivalenza tra
tripoli di resistenze
J
RBC ( R AB R AC )
J ( RB RC )
R AB RBC R AC
Condizioni di equivalenza tra
tripoli di resistenze
R AC ( R AB RBC )
J
J ( R A RC )
R AB RBC R AC
Equazioni delle trasformazioni
triangolo-stella e stella-triangolo
Eliminando J dalle equazioni precedenti si ottiene il
sistema:
R AB ( RBC R AC )
R A RB
R AB RBC R AC
RBC ( R AB R AC )
RB RC
R AB RBC R AC
R AC ( R AB RBC )
R A RC
R AB RBC R AC
Equazioni delle trasformazioni
triangolo-stella e stella-triangolo
Trasformazione triangolo-stella
R AB RBC
RB
R0
R AB R AC
RA
R0
RBC R AC
RC
R0
dove
R0 R AB RBC R AC
Trasformazione stella-triangolo
R AB R A RB G0
G0
1
1
1
R A RB RC
RBC RB RC G0
R AC R A RC G0
dove
Un caso particolare
R 3RY
R
Ry
3
R A RB RC RY
R AB
3
R
3RY
RY
2
Y
R AB R A RB G0 R G0
2
Y
RBC R AC R AB R
G0
1
1
1
3
R A R B RC RY
Analisi di una rete elettrica
LKT per le maglie 1, 2, 3
1)
E1 R1 I1 R3 I 3
2)
E2 R2 I 2 R3 I 3
3)
E1 E2 R1 I1 R2 I 2
LKC per il nodo A (o B)
I1 I 2 I 3 0
Analisi di una rete elettrica,
grafo, albero e coalbero
Data una generica rete elettrica di bipoli lineari:
Il grafo è costituito da l lati e n nodi.
L’albero è costituito da n-1 lati e n nodi
Il coalbero è costituito da l-(n-1) lati
Esempi di grafi, alberi e coalberi
l=3
n=2
Esempi di grafi, alberi e coalberi
l=10
n=6
Analisi di reti resistive con
sorgenti di tensione
Data la generica rete, con l lati ed n nodi:
il calcolo delle correnti si effettua risolvendo il sistema
di l eq. lineari nelle n incognite Ik costituito da:
m
l-(n-1) LKT
() E
LKC
k
( ) Rk I k
1
1
m
n-1
m
I
1
k
0
Un esempio numerico
R1 R2 R3 20
E1=30 V
Sistema risolvente
Forma matriciale
20 I 1 20 I 3 30
20 0 20 I 1 30
0 20 20 I 60
2
1 1 1 I 3 0
20 I 2 20 I 3 60
I1 I 2 I 3 0
E2=60 V
Risultato
I1=0
I2=1,5 A
I3=1,5 A
Una rete con sorgenti di
tensione e di corrente
R1 R2 R3 20
E1=30 V
J=2 A
I3 J
R1 I1 R2 I 2 E1
I1 I 2 J
20I1 20I 2 30
I1 I 2 2
R1
1
R2 I1 E1
1 I 2 J
I1=-0,25 A
I 1 R1
I 1
2
I2=1,75 A
1
R2 E1
1 J
Analisi di reti con sorgenti di
tensione e di corrente
Data la generica rete, con sorgenti di tensione e di
corrente, con n nodi ed l lati (l è definito non
considerando i lati contenenti i generatori di corrente in
cui la corrente è nota), il calcolo delle l correnti incognite
Ik si effettua risolvendo il sistema di l eq. lineari,
linearmente indipendenti costituito da:
m
l-(n-1) LKT
n-1
LKC
() E
m
k
( ) Rk I k
1
1
m
r
() I
1
k
( ) J k
1
Sovrapposizione degli effetti
R1
1
R2 I1 E1
1 I 2 J
A( 22) I ( 21) H ( 21)
H
E1 E1 0
H ' H "
J 0 J
I A1 H A1 H ' A1 H " I ' I "
I '1 R1
I ' 1
2
1
R2 E1
1 0
I "1 R1
I " 1
2
1
R2 0
1 J
I3 J
Sovrapposizione degli effetti, un
esempio numerico
R1 R2 R3 20
I1=I’1+I”1=-0,25 A
E1=30 V
J=2 A
I2=I’2+I”2=1,75 A
I3=I’3+I”3=2 A
I '1 I ' 2
E1
0,75
R1 R2
I '3 0
R2
I "1 J
1
R1 R2
I "3 J 2
I "2 J
R1
1
R1 R2
%
Le potenze in gioco
Potenza erogata da E1:
Pe1=E1 I1=-7,5 W
Potenza erogata da J:
PeJ=VJJ=150 W
Potenze assorbite dalle
resistenze:
PR1=R1I12=1,25 W
PR2=R2I22=61,25 W
PR3=R2I32=80 W
Prtot=142,5 W
V j R3 I 3 R2 I 2
VJ=75 V
Sovrapposizione degli effetti, un
esempio numerico
R1 R2 R3 20
E1=30 V
E2=60 V
Req=R1+R2//R3=30 Ω
E
I '1 1
Req
I’1= 1 A
R3
I ' 2 I '1
0,5 A
R2 R3
I '3 I '1
R2
0,5 A
R2 R3
%
Sovrapposizione degli effetti, un
esempio numerico
Req=R2+R1//R3=30 Ω
I "2
E2
2
Req
I1=I’1+I”1=0
R2
I "3 I "2
1
R2 R3
I2=I’2+I”2=1,5 A
Pe2=60x1,5=90 W
I "1 I "2
R3
1
R2 R3
I3=I’3+I”3=1,5 A
PRtot=20x1,52+20x1,52=90 W
Non applicabilità della sovrapposizione
degli effetti al calcolo delle potenze
Posto:
Pk' Rk I k' 2
Pk" Rk I k"2
la potenza Pk assorbita dalla resistenza Rk non è pari
alla somma di P’k e P”k; infatti:
Pk Rk I k2 Rk ( I k' I k" ) 2 Pk' Pk" 2 Rk I k' I k"
Principio di conservazione delle
potenze elettriche
Ipotesi: La stessa
convenzione dei segni su
tutti gli l lati della rete.
Siano P1,.. Pi,…Pn gli n
nodi della rete
l
Tesi Vk I k 0
Generico bipolo costituente il
k-esimo lato della rete
1
l
U ( P"
1
l
k
) I k U ( P' k ) I k 0
1
Somma parziale relativa
al nodo Pi
U Pi ( I i1 I i 2 .... I ih ....I il' ) 0
i
Vk U ( P"k ) U ( P' k )
Una formulaz. del principio di
conservazione nelle reti lineari
P P P
Ei
i
Ji
i
Ri
i
0
PRi R I
2
i i
2
P
P
R
I
Ei Ji i i
i
i
La somma delle potenze erogate dai generatori
di tensione e di corrente è eguale alla somma
delle potenze assorbite dalle resistenze
i
Un corollario dei principi di
Kirchhoff
Ipotesi Nel generico
nodo P’ confluiscono solo
bipoli passivi
Tesi Tra i nodi contigui
esiste almeno un nodo P”
a potenziale U≥U(P’) e
almeno uno a potenziale
U≤U(P’).
Da questo corollario
scaturisce il principio di
non amplificazione delle
tensioni.
Vk I k 0
4
I
k
0
1
Se I1, I2>0 si ha V1,V2≥0 e
U(P”1)≤U(P’) e U(P”2)≤U(P’)
Se I3, I4<0 si ha V3,V4 ≤ 0 e
U(P”3) ≥ U(P’) e U(P”4) ≥ U(P’)
Principio di non amplificazione
delle tensioni
Tale principio prevede che ai capi dell’unico lato attivo di
una rete in regime stazionario, in cui vi siano tutti lati
passivi tranne uno, è applicata la tensione massima.
Si consideri infatti l’insieme di n elementi costituito dai
potenziali degli n nodi della rete. Per il precedente
corollario il potenziale dei nodi in cui confluiscono solo
lati passivi non può essere né il massimo né il minimo di
tale insieme. Conseguentemente i potenziali massimo e
minimo devono essere relativi ai nodi posti agli estremi
dell’unico lato attivo.
Analisi di reti con sorgenti di
tensione e di corrente
Data la generica rete con n nodi ed l lati il calcolo delle
l correnti incognite Ik si effettua risolvendo il sistema di l
eq. lineari, linearmente indipendenti costituito da:
m
m
l-(n-1) LKT () E k () Rk I k
1
1
m
n-1
LKC
I
r
k
J k
1
1
A(ll ) I (l1) H (l1)
Vk Ek Rk I k A'(ll ) V (l1) H '(l1)
Rk
Ek
Vk
Ik
Metodo dei potenziali nodali
Rk
Tk
Ik
Ek
Vk U Sk U Tk
Vk Ek Rk I k
I k ( Ek U Sk U Tk )Gk
G k 1 / Rk
Sk
Sostituendo le correnti
nelle n-1 LKC:
m
I
1
r
k
J k
1
si ha il sistema di n-1 eq.
nelle n incognite Upk:
m
(E
1
r
k
U Sk U Tk )Gk J k
1
Se poniamo eguale a
zero il potenziale di uno
degli n nodi, si ottiene:
A"( n1)( n1) U ( n1)1 H "( n1)1
Metodo dei potenziali nodali, la
formula di Millmann
La LKC
fornisce
n
I
i
0
1
dove:
I i ( Ei U A )Gi
1
Gi
Ri
n
n
E i Gi U A Gi
1
n
1
U A VAB
EG
i
i
1
n
G
i
1
UB 0
Formula di Millmann: un
esempio numerico
R1 R2 R3 20
E1=30 V
E2=60 V
G1=G2=G3=G=0,05 Ω-1
UB 0
3
UA
E G
1
1
3
G
1
i
i
E1G E 2 G
30 V
3G
I1=(E1-UA)G1=0
I2=(E2-UA)G2=1,5 A
I3=(-UA)G3=-1,5 A
Teorema di Thévenin: enunciato
Se s’isola un lato AB di
una rete lineare, il bipolo
a monte dei morsetti A,B
è equivalente ad un
bipolo di Thévenin, in cui
V0 è la tensione a vuoto
tra A e B e Req è la
resistenza equivalente
dello stesso bipolo reso
passivo.
Req
V0
Teorema di Thévenin:
dimostrazione
V " Req I "
%
Teorema di Thévenin:
dimostrazione
V V 'V " V0 Req I "
I I 'I " 0 I "
V V0 Req I
Req
V0
Teorema di Thévenin: una
conseguenza
V0
I
R Req
R
V V0
R Req
Un esempio numerico
R1 R2 R3 20
E1=30 V
I3
I
E2 E1
0,75
R1 R2
A
E2=60 V
V0
45
1,5 A
R3 Req 20 10
V0 E2 R2 I 45 V
Req=R1//R2=10 Ω
Teorema di Norton: enunciato
Se s’isola un lato AB di
una rete lineare, il bipolo
a monte dei morsetti A,B
è equivalente ad un
bipolo di Norton, in cui Icc
è la corrente di corto
circuito tra A e B e Req è
la resistenza equivalente
dello stesso bipolo reso
passivo.
Req
Teorema di Norton:
dimostrazione
Caratteristica comune ai bipoli
di Thévenin e Norton
Req
V0
Teorema di Norton: una
conseguenza
I I cc
Req
R Req
V I cc
Req R
R Req
Un esempio numerico
R1 R2 R3 20
E1=30 V
I 3 I cc
Icc=E1/R1+E2/R2=4,5 A
Req
R Req
E2=60 V
4,5
10
1,5 A
20 10
Req=R1//R2=10 Ω