DOPPI BIPOLI
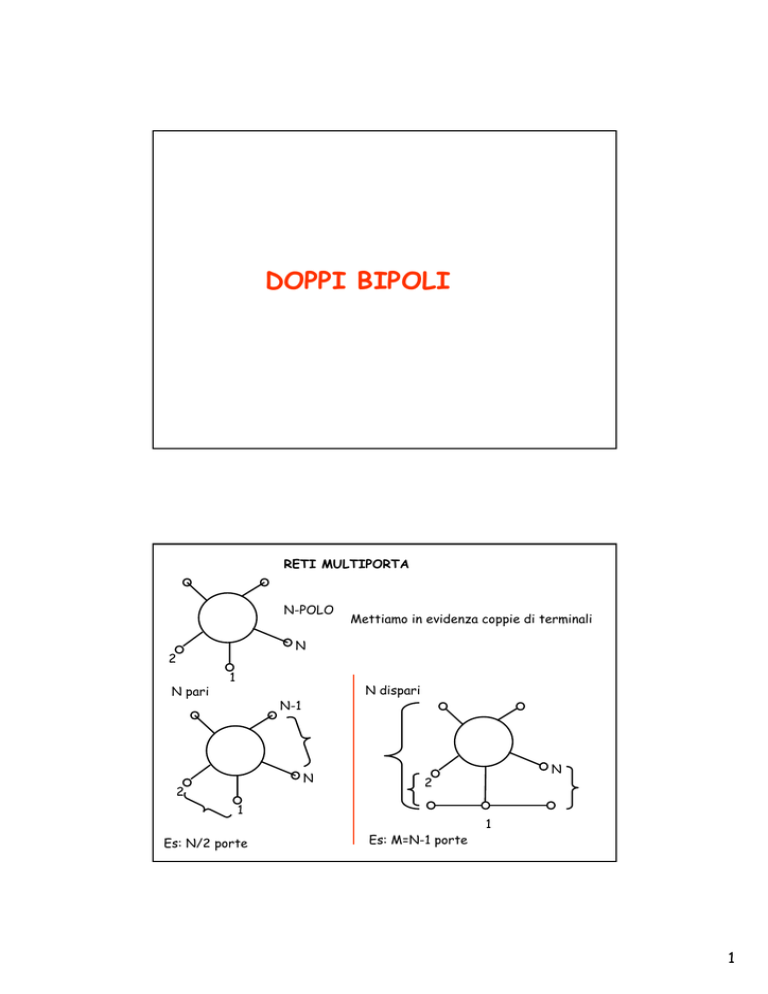
RETI MULTIPORTA
N-POLO
N
2
N pari
Mettiamo in evidenza coppie di terminali
1
N dispari
N-1
N
2
1
Es: N/2 porte
N
2
Es: M=N-1 porte
1
1
RETI MULTIPORTA (Cnt.)
Le coppie di morsetti sono chiamate PORTE e ad esse si
possono collegare solo bipoli
In generale dato un M-porte: M+1≤N≤2M
M
1
1’
M’
i1
consentito
1
i1
interdetto
2
2’
SI RITROVANO I TEOREMI DI THEVENIN E DI
NORTON IN FORMA MATRICIALE
Hp: componente definito su base corente
I1 V1
I1j
E k V2
I2
Per il principio di
sovrapposizione degli
effetti:
Vi = Z i1 I1 + Z i 2 I 2 + ⋅ ⋅ + Z iM I M +
I3
+
∑α
k
ik E k
+
∑Z
j
ij A j
Chiamando Ei la quantità tra parentesi e generalizzando:
V 1 Z11 ⋅ ⋅ Z1M I 1 E 1
V = ⋅ = ⋅
⋅⋅
⋅ ⋅ ⋅ + ⋅
V M Z
⋅ ⋅ Z MM I M E M
M1
[]
V = Z I + E
2
Teorema di Thevenin generalizzato:
E2
E1
V = [Z ]⋅ I + E
Ei: tensione alla porta i-sima quando
le porte sono lasciate aperte
Passivo
1
[Z]
[Z]: matrice di impedenza che
caratterizza lo M-porte passivato
E3
Teorema di Norton generalizzato:
A1
Passivo
1
[Z]
A2
I = [Y ]⋅ V + A
Ai: corrente di corto circuito sulla
porta i-sima
[Y]: matrice di ammettenza che
caratterizza lo M-porte passivato
A3
1
[Z ]Thevenin = [Y ]−Norton
CARATTERIZZAZIONE DEGLI M-PORTA INERTI
Matrice di Impedenza
Solo se il componente e’ definito su base corrente
3
Una rete a T in funzione dei parametri impedenza.
Esempio
L1
V1
I1
Z11 =
R
I2
C
jϖ (L1 + L2 )
1 − ϖ 2C (L1 + L2 )
Z 21 = Z12 =
Z 22 =
L2
(1 −ϖ
V2
V1 = Z11 I1 + Z12 I 2
V2 = Z 21 I1 + Z 22 I 2
+R
jϖL2
1 − ϖ C (L1 + L2 )
2
2
)
L1C jϖL2
1 − ϖ 2 C (L1 + L2 )
4
ESEMPIO
Determinare i parametri Z
m=2/3
Lasciamo aperta la porta 2 e
alimentiamo la porta 1 con un
generatore di corrente
I1
I
V2
I 1 − m ⋅ V2 = I
V1 = 4 I1 + 5I ⇒
V = 3I
2
V
V2
1
Z 21 = 2
=
⋅
+
=
+
⋅
V
m
V
m
V
2
2
I1
1
3
3
⇒
V
V = 4 I + 5V2 = 4 I + 5 I
Z11 = 1
1
1
1
1
3
3
I1 I
= 1Ω
I 2 =0
=
2 =0
17
Ω
3
Matrice di ammettenza
Solo se il componente e’ definito su base tensione
Se il componente e’ definito su base tensione e su base corrente:
[Z ] = [Y ]−1
5
Una rete a Π in funzione dei parametri ammettenza.
Esempio
[Z] non esiste
1
[Y ] = Z1
−
Z
Z
Esempio
1
Z
1
Z
−
[Y] non esiste
Z
[Z ] =
Z
Z
Z
Z
6
Matrici Ibride
1. Base di definizione
I1
V 2
V 1 h11
=
I 2 h21
h12 I 1
⋅
h22 V 2
Tipica dei transistori
2. Base di definizione
V 1
I 2
I 1 g11
=
V 2 g 21
g12 V 1
⋅
g 22 I 2
Tipica dei tubi a vuoto
I parametri [h] e [g] non hanno omogeneità dimensionale
Doppio bipolo equivalente nella formulazione ibrida h.
Doppio bipolo equivalente nella formulazione ibrida g.
7
TRANSISTOR
Uso dei parametri h
per descrivere un
transistore.
Un doppio bipolo
equivalente
Il doppio bipolo
equivalente semplificato
con hre = 0 and hoe = 0.
Es: Amplificatore a transistor per piccoli segnali
per garantire la corretta
polarizzazione del transistor:
300 < Rc < 5000 Ω
Av =
v0
vin
guadagno di piccolo
segnale
Un circuito equivalente dell’amplificatore a transistore
Le schede tecniche del transistor lo caratterizzano specificando i
parametri della matrice [h]
8
Matrici di Trasmissione
Se il doppio bipolo e’ definito dalla conoscenza delle variabili a una sola
porta si può caratterizzare con le metrici di trasmissione diretta T e
inversa T’
1. Diretta
2. Inversa
V 1
V 2 A B V 2
= [T ]⋅
=
⋅
I 1
− I 2 C D − I 2
V 2
V 1 A' B' V 1
= [T ']⋅
=
⋅
I 2
− I 1 C ' D' − I 1
Quando esistono le relative basi di definizione si possono ricavare
gli elementi di una matrice a partire dalla conoscenza di quelli di
un’altra
COLLEGAMENTO DI DOPPI BIPOLI
1. SERIE
Stessa corrente alle porte
V A = [Z A ]⋅ I A
V B = [Z B ]⋅ I B
V = V A +V A
IA = IB = I
V = [Z A ]⋅ I A + [Z B ]⋅ I B = ([Z A ] + [Z B ])I
[Z ] = [Z A ] + [Z B ]
SI SOMMANO I PARAMETRI Z DI CIASCUN DOPPIO BIPOLO
9
COLLEGAMENTO DI DOPPI BIPOLI
2. PARALLELO
Stessa tensione alle porte
I A = [Y A ]⋅ V A
I B = [YB ]⋅ V B
I = IA +IB
I = [YA ]⋅ V A + [YB ]⋅ V B = ([YA ] + [YB ])V
V A =V B =V
[Y ] = [YA ] + [YB ]
SI SOMMANO I PARAMETRI Y DI CIASCUN DOPPIO BIPOLO
3. Collegamento in Cascata
La porta di uscita di un
doppio bipolo e’ collegata
con la porta di ingresso
del successivo
V 2A
V 1 A
= [T A ]⋅
I 1 A
− I 2 A
V 1B
V 2B
= [TB ]⋅
− I 2 B
I 1B
V 1 V 1 A V 2 B V 2
=
;
=
I 1 I 1 A − I 2 B − I 2
V 2 A V 1B
=
I 2 A − I 1B
V 1
V2
= [T A ]⋅ [TB ]⋅
I 1
− I 2
[T ] = [TA ]⋅ [TB ]
SI MOLTIPLICANO LE MATRICI DI TRASMISSIONE
MANTENENDO L’ORDINE DELLA CASCATA
10
Equivalenza di doppi bipoli
Due doppi bipoli sono equivalenti quando hanno gli stessi valori degli
elementi delle rispettive matrici che li definiscono
Trasformazione T- Π
A
ZA
Triangolo-Stella
B
ZB
ZC
C
A
.
.
ZA =
C
B
ZAB
ZCA
(o Stella – Triangolo)
.
.
.
;ZB =
.
ZC =
;
Z∆
.
.
.
Z BC Z AB
Z∆
ZBC
C
.
Z AB Z CA
.
Z CA Z BC
.
;
Z∆
C
.
.
.
.
Z ∆ = Z AB + Z BC + Z CA
Stella - Triangolo
.
Y AB =
.
.
Y AYB
.
Yo
.
; Y BC =
.
.
YBYC
.
Yo
.
; Y CA =
.
.
YC Y A
.
.
.
.
.
;Y o = Y A + Y B + Y C
Yo
11