Regime sinusoidale
Sinusoidi
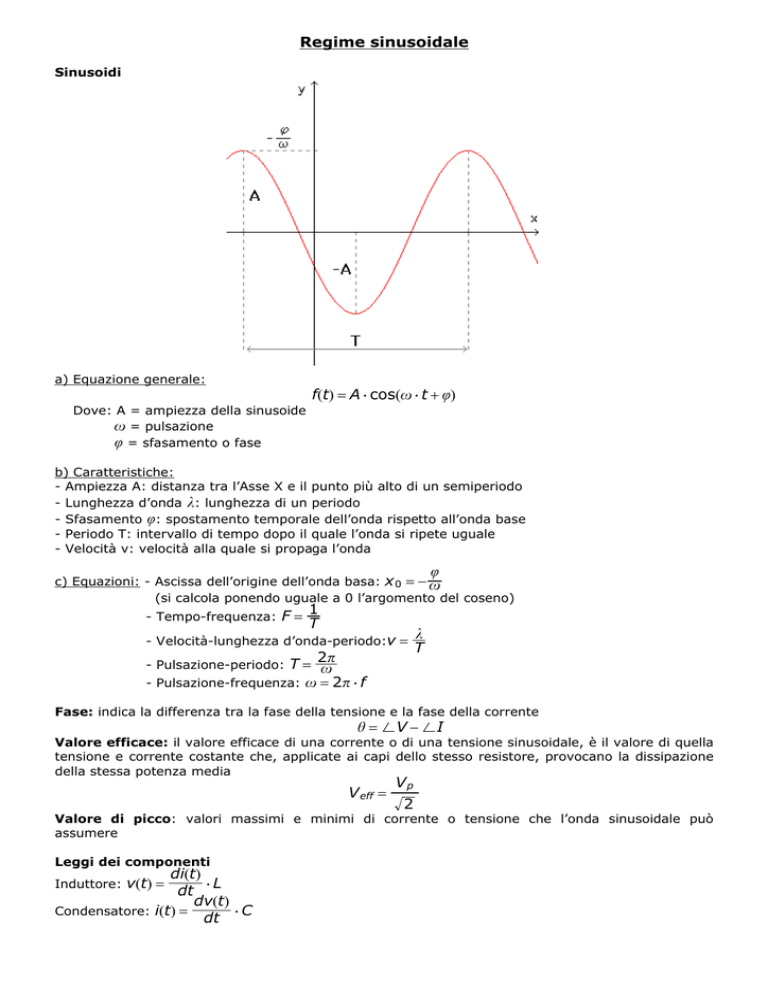
a) Equazione generale:
Dove: A = ampiezza della sinusoide
* = pulsazione
' = sfasamento o fase
f(t) = A $ cos(* $ t + ')
b) Caratteristiche:
- Ampiezza A: distanza tra l’Asse X e il punto più alto di un semiperiodo
- Lunghezza d’onda : lunghezza di un periodo
- Sfasamento ': spostamento temporale dell’onda rispetto all’onda base
- Periodo T: intervallo di tempo dopo il quale l’onda si ripete uguale
- Velocità v: velocità alla quale si propaga l’onda
'
c) Equazioni: - Ascissa dell’origine dell’onda basa: x 0 = − *
(si calcola ponendo uguale a 0 l’argomento del coseno)
- Tempo-frequenza: F =
1
T
- Velocità-lunghezza d’onda-periodo:v =
2
- Pulsazione-periodo: T = *
- Pulsazione-frequenza: * = 2 $ f
T
Fase: indica la differenza tra la fase della tensione e la fase della corrente
= øV − øI
Valore efficace: il valore efficace di una corrente o di una tensione sinusoidale, è il valore di quella
tensione e corrente costante che, applicate ai capi dello stesso resistore, provocano la dissipazione
della stessa potenza media
V eff =
Vp
2
Valore di picco: valori massimi e minimi di corrente o tensione che l’onda sinusoidale può
assumere
Leggi dei componenti
di(t)
$L
dt
dv(t)
Condensatore: i(t) =
$C
dt
Induttore: v(t) =
Diagramma dei vettori rotanti
^
X
^
IXI
^
IXI.sen θ
θ
^
IXI.cos θ
Nome
In fase
Rapporto tra fasi differenti nei grafici
Differenza di
Diagramma dei vettori
fase
rotanti
= 0
Grafico del tempo
^
X
θ
In
quadratura
di fase
= 90 o
^
X2
^
X1
θ2
θ1
In
controfase
---In
opposizione
di fase
= 180 o
θ2
^
X1
θ1
^
X2
^
^
Fase nella resistenza: V= R $ I
u la corrente e la tensione sono in fase
V0
Fase nell’induttore: I = L$* sen(*t − )
2
fase nella formula: −
fase sul grafico:
2
2
u la corrente è in ritardo di 90° rispetto alla tensione
Fase nel condensatore:I = (V 0 $ * $ C) $ sen(*t + )
2
fase nella formula: +
2
fase sul grafico:−
2
u la corrente è in anticipo di 90° rispetto alla tensione
Elementi nel bipolo
induttori
Schema per i GRAFICI
Fase
= +90
o
condensatori
0 < < 90 o
=0
−90 o < < 0
= −90 o
condensatori+induttori+resistenze
fase variabile
induttori + resistenze
resistenze
condensatori+resistenze
Nome
bipolo reattivo
bipolo puramente induttivo
bipolo induttivo
bipolo puramente resistivo
bipolo capacitivo
bipolo puramente reattivo
bipolo puramente capacitivo
La fase di un bipolo LCR è sempre compresa tra -90° e + 90°
Nomi
Z = impedenza - misurata in Ohm
1
Y= z = ammettenza - misurata in Siemens












