Istituto Tecnico Industriale “Verona Trento” - Messina
Storia
Euclide (Ευκλείδης), nato ad Alessandria d'Egitto
intorno al 365 a.C., fu un matematico greco.
Euclide di Alessandria (da non confondere con
Euclide di Megara che visse un secolo prima e
che era un filosofo) è menzionato in un brano
Di Pappo, ma la testimonianza più importante
viene da Proclo, che lo colloca tra i pù giovani
discepoli di Platone.
Della sua vita si conosce ben poco e taluni mettono
indubbio che questo nome denoti una persona reale,
indicando bensì un gruppo di studiosi che si siano impegnati nella stesura
di un trattato rigoroso e relativamente completo. L'opinione prevalente,
però, considera Euclide una persona reale. Si dice sia stato discepolo
di Platone ad Atene. Trasferitosi in seguito ad Alessandria d'Egitto all'epoca
di Tolomeo I, vi fondò una scuola di matematica che rimase illustre per secoli.
Aneddoti
Su Euclide esistono un paio di aneddoti, i quali pur non
avendo un fondamento storico, si avvicinano bene al
carattere dell’autore de “Gli Elementi”.
Nel primo viene detto che il re Tolomeo I chiese ad
Euclide se non vi fosse un mezzo più breve per imparare
la geometria ed egli rispose che “non esistono vie
regie in geometria”.
Questa storia sottolinea il grande rigore che permea
tutta l’opera di Euclide .
Nel secondo si narra di un discepolo che dopo aver
imparato i primi teoremi chiese ad Euclide: “Quale utile
ricaverò imparando queste cose?”. Euclide diede ordine ad un servo di
dare le monete al discepolo perché quest’ultimo voleva trarre profitto
da quel che imparava.
Quest’ultimo aneddoto allude invece al carattere teorico dell’opera
infatti Euclide non presenta le applicazioni pratiche delle sue teorie.
Opere
Gli Elementi (in greco Στοιχεῖα) di Euclide sono la
più importante opera sulla matematica giuntaci
dalla cultura greca antica. Composti tra il IV e il
III secolo a.c., rappresentano un quadro completo
e definito dei principi della geometria noti al tempo.
La geometria che si studia nelle scuole ancora oggi
è la geometria euclidea perché questa è il migliore
strumento che abbiamo a disposizione per interpretare
la realtà che ci circonda, visto che essa nasce proprio
dall’osservazione della realtà.
L'opera consiste in 13 libri: i primi 6 riguardanti la
geometria piana, tre sulla teoria dei numeri, il
decimo libro sulla teoria degli incommensurabili
e gli ultimi tre sulla geometria solida.
Alcune edizioni più antiche attribuiscono ad Euclide
anche due ulteriori libri che la critica moderna assegna
però ad altri due autori. I diversi libri sono
strutturati in definizioni proposizioni (enunciati
che potremmo anche chiamare teoremi).
Delle proposizioni vengono fornite
e dimostrazioni. L'arte del calcolo non
è inclusa: questa, infatti, non
faceva parte dell’educazione superiore.
E neppure lo studio neppure lo studio
delle coniche o delle curve piane superiori
fa parte dell’opera, poiché costituiva
una branca più avanzata della matematica.
Particolarmente importante è quest’opera per
lo studio, basato su un metodo che attraverso
il ragionamento logico deduttivo va alla ricerca
di regole generali, degli assiomi e dei postulati.
Gli assiomi sono proposizioni che enunciano proprietà
Che non si possono dimostrare, ma di solito
sono così evidenti che nessuno si metterebbe
a discutere la loro veridicità. Senza di essi non
si potrebbe dimostrare niente, saremmo costretti
ad accettare le proprietà affermate dai teoremi
credendoci finché ci sostiene l’evidenza, ma senza
poterne garantire una volta per tutte la veridicità
in modo inattaccabile e inconfutabile.
Essi perciò sono come una vera e propria
impalcatura di sostegno per tutto il sistema
della geometria.
Un assioma che viene considerato indispensabile viene chiamato postulato.
Sicuramente il postulato più famoso è il V, detto anche postulato delle
rette parallele (anche se l'enunciato non le cita).
La negazione di questo postulato ha portato, nel XIX secolo, allo sviluppo
delle geometrie non euclidee.
Legata al V postulato è la definizione XXXIX del libro I:
In un piano, una retta che intersechi due rette parallele forma con esse
angoli alterni uguali fra loro, angoli esterni uguali agli angoli interni e opposti,
e dalla stessa parte angoli interni la cui somma è uguale a due retti.
Euclide scrisse anche altre opere come i “Dati” e la
“Divisione della figura”, “L’ottica” e la “Catottrica”
però deve la sua celebrità a “Gli Elementi”,
che è un’opera davvero importante e che a buon
diritto tramanda attraverso i secoli il suo nome.
Per saperne di più sui postulati
sulle rette parallele
In figura 1 la retta r è fissa mentre la retta s può ruotare in
senso antiorario attorno al punto P. Indichiamo con Q il punto in cui
r ed s si incontrano.
Man mano che s ruota si vede che il punto Q si allontana verso est
sulla retta r (fig. 2).
Il punto Q si muove con continuità su r: piccole rotazioni di
s determinano piccoli spostamenti di Q (e viceversa). Q assume via
via tutte le posizioni possibili su r, "passa" per tutti i punti di r.
Il punto Q dunque si allontana sempre più sulla retta r. Si intuisce
però che esiste una (e una sola) situazione in cui sembra proprio che
le due rette non si intersechino e quindi Q non esista. In
questa situazione le due rette si dicono parallele (fig. 3).
Continuando a ruotare s ci accorgiamo che il punto Q ricompare su
r, questa volta però Q è a ovest.
Eccoci arrivati a un punto cruciale. Nella geometria euclidea si assume,
assecondando l'intuizione, che per un punto P non appartenente alla
retta r passi una e una sola retta s parallela a r (tale cioè che r e s non
si incontrino). Tale assunzione non è altro che il quinto postulato di
Euclide.
Dimostrazione dell’infinità dei
numeri primi
Un numero maggiore dell'unità si dice
primo se ha solo due divisori distinti:
1 e se stesso.
Tra 1 e 10 ci sono 5 numeri primi;
Tra 10 e 100 ce ne sono 21;
Tra 9.999.900 e 10.000.000 ce ne sono 9;
Tra 10.000.000 e 10.000.100 ce ne sono 3.
Questa è la legge di rarefazione dei
numeri primi. Secondo questa legge si
può pensare che i numeri primi siano in
numero finito, ma non è così, infatti,
Euclide dimostrò che i numeri primi
sono infiniti.
Dimostrazione (metodo indiretto):
Si suppone che i numeri primi siano in numero finito.
Esiste allora il numero primo più grande di tutti (MAX).
Se si esegue il prodotto tra MAX e tutti i numeri primi che
lo precedono e si aumenta di 1 il risultato, si ottiene un nuovo
numero primo N più grande di MAX: infatti dividendo N per
ciascun numero primo si ottiene sempre resto 1.
Questa è un’assurdità perché è in contrasto con il fatto che MAX sia
il più grande numero primo. Perciò si conclude che i numeri primi
sono infiniti.
Teoremi
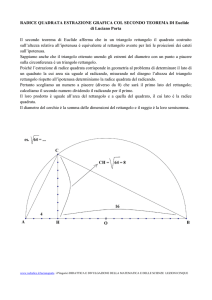
Primo teorema di Euclide
In ogni triangolo rettangolo,
il quadrato costruito su un
cateto è equivalente
al rettangolo che ha per
lati l'ipotenusa e la proiezione
del cateto sull'ipotenusa.
Nel disegno il quadrato Q è
equivalente,ossia ha la stessa area,
del rettangolo R
In formula si ha: AB2 = BC · BH
Dimostrazione
Prima dimostriamo che il triangolo ABC
è uguale al triangolo EBT. Facendo
riferimento alla figura, i due triangoli hanno
AB=BE, l'angolo ABC uguale all'angolo TBE
(perché complementari dello stesso angolo ABT).
Per il criterio di congruenza dei triangoli
rettangoli i due triangoli sono uguali.
Se ne deduce che BC=BT.
Il quadrato Q e il parallelogrammo P hanno
la stessa base AB e la stessa altezza AD,
che è la distanza tra le rette parallele AB e EL,
quindi Q e P sono equivalenti.
Il parallelogrammo P e il rettangolo R hanno le basi BT e BM uguali e
l'altezza BH in comune, perché distanza tra le rette parallele TM e LK.
Per la proprietà transitiva dell'equivalenza si ha che Q è equivalente a R.
Secondo teorema di Euclide
In ogni triangolo rettangolo, il quadrato
costruito sull'altezza relativa
all'ipotenusa è equivalente al rettangolo
che ha per lati le proiezioni dei cateti
sull'ipotenusa Nel disegno Q1 è equivalente
aR
In formula AH2 = BH · HC
Descrizione della figura
Il triangolo ABC è rettangolo in A.
Q1 è il quadrato costruito sull'altezza
AH relativa all'ipotenusa.
Q2 è il quadrato costruito sulla proiezione
BH del cateto AB.
Q3 è il quadrato costruito sul cateto AB.
Il rettangolo BHKM ha come lati la proiezione
BH del cateto AB sull'ipotenusa e BM=BC.
Il rettangolo R ha come lati le proiezioni
dei cateti sull'ipotenusa.
LM = BM - BL = BC - BH = HC.
Dimostrazione
Per il primo teorema di Euclide applicato
al triangolo rettangolo ABCQ3 è equivalente
a Q2 + R.Per il teorema di Pitagora applicato
al triangolo rettangolo ABHQ3 è equivalente
a Q2+Q1Per la proprietà transitiva
dell'equivalenza si ottieneQ2+Q1 è equivalente
a Q2+RSe ne conclude cheQ1 è equivalente a R
Della morte di Euclide si sa ben poco si presume che morì attorno al 275 a.c.