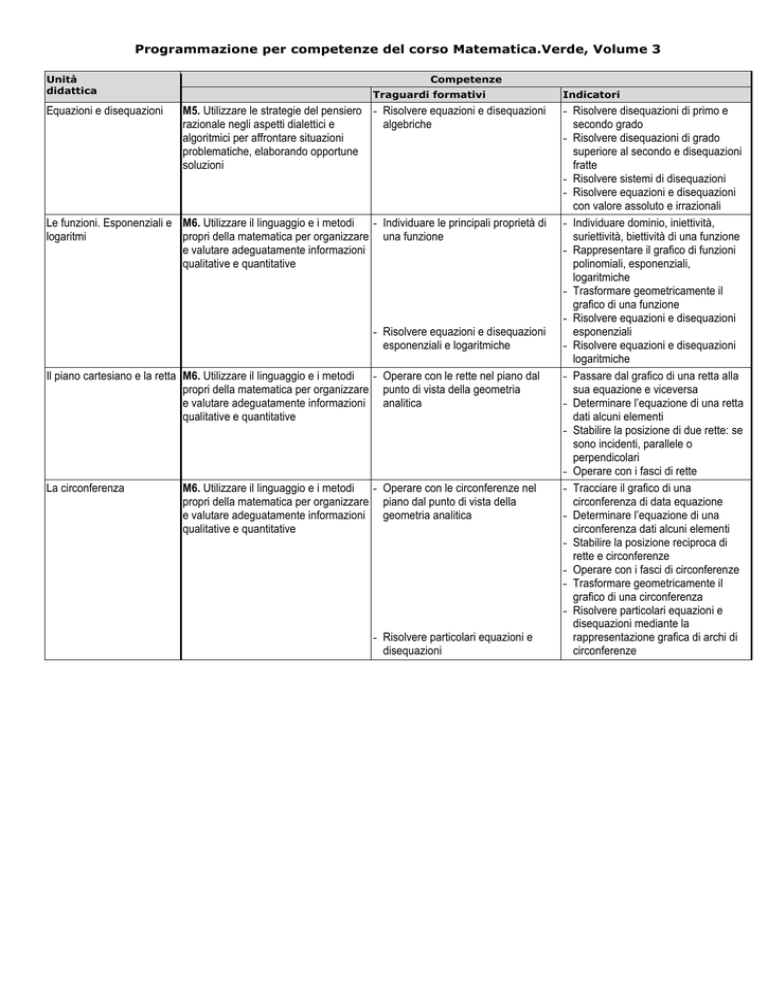
Programmazione per competenze del corso Matematica.Verde, Volume 3
Unità
didattica
Equazioni e disequazioni
Competenze
Traguardi formativi
M5. Utilizzare le strategie del pensiero - Risolvere equazioni e disequazioni
razionale negli aspetti dialettici e
algebriche
algoritmici per affrontare situazioni
problematiche, elaborando opportune
soluzioni
Le funzioni. Esponenziali e M6. Utilizzare il linguaggio e i metodi - Individuare le principali proprietà di
logaritmi
propri della matematica per organizzare una funzione
e valutare adeguatamente informazioni
qualitative e quantitative
- Risolvere equazioni e disequazioni
esponenziali e logaritmiche
Il piano cartesiano e la retta M6. Utilizzare il linguaggio e i metodi - Operare con le rette nel piano dal
propri della matematica per organizzare punto di vista della geometria
e valutare adeguatamente informazioni analitica
qualitative e quantitative
La circonferenza
M6. Utilizzare il linguaggio e i metodi - Operare con le circonferenze nel
propri della matematica per organizzare piano dal punto di vista della
e valutare adeguatamente informazioni geometria analitica
qualitative e quantitative
- Risolvere particolari equazioni e
disequazioni
Indicatori
- Risolvere disequazioni di primo e
secondo grado
- Risolvere disequazioni di grado
superiore al secondo e disequazioni
fratte
- Risolvere sistemi di disequazioni
- Risolvere equazioni e disequazioni
con valore assoluto e irrazionali
- Individuare dominio, iniettività,
suriettività, biettività di una funzione
- Rappresentare il grafico di funzioni
polinomiali, esponenziali,
logaritmiche
- Trasformare geometricamente il
grafico di una funzione
- Risolvere equazioni e disequazioni
esponenziali
- Risolvere equazioni e disequazioni
logaritmiche
- Passare dal grafico di una retta alla
sua equazione e viceversa
- Determinare l’equazione di una retta
dati alcuni elementi
- Stabilire la posizione di due rette: se
sono incidenti, parallele o
perpendicolari
- Operare con i fasci di rette
- Tracciare il grafico di una
circonferenza di data equazione
- Determinare l’equazione di una
circonferenza dati alcuni elementi
- Stabilire la posizione reciproca di
rette e circonferenze
- Operare con i fasci di circonferenze
- Trasformare geometricamente il
grafico di una circonferenza
- Risolvere particolari equazioni e
disequazioni mediante la
rappresentazione grafica di archi di
circonferenze
Programmazione per competenze del corso Matematica.Verde, Volume 3
Unità
didattica
La parabola
Competenze
Traguardi formativi
M6. Utilizzare il linguaggio e i metodi - Operare con le parabole nel piano
propri della matematica per organizzare dal punto di vista della geometria
e valutare adeguatamente informazioni analitica
qualitative e quantitative
L’ellisse e l’iperbole
M6. Utilizzare il linguaggio e i metodi propri della matematica per organizzare
e valutare adeguatamente informazioni
qualitative e quantitative
Le funzioni goniometriche
M6. Utilizzare il linguaggio e i metodi propri della matematica per organizzare
e valutare adeguatamente informazioni
qualitative e quantitative
-
Le equazioni e le
M5. Utilizzare le strategie del pensiero disequazioni goniometriche razionale negli aspetti dialettici e
algoritmici per affrontare situazioni
problematiche, elaborando opportune
soluzioni
-
Indicatori
- Tracciare il grafico di una parabola di
data equazione
- Determinare l’equazione di una
parabola dati alcuni elementi
- Stabilire la posizione reciproca di
rette e parabole
- Trovare le rette tangenti a una
parabola
- Operare con i fasci di parabole
- Trasformare geometricamente il
grafico di una parabola
- Risolvere particolari equazioni e
disequazioni mediante la
Risolvere particolari equazioni e
rappresentazione grafica di archi di
disequazioni
parabole
Operare con le ellissi e le iperboli nel - Tracciare il grafico di una ellisse e di
piano dal punto di vista della
una iperbole di date equazioni
geometria analitica
- Determinare l’equazione di una
ellisse e di una iperbole dati alcuni
elementi
- Stabilire la posizione reciproca di
rette ed ellissi e di rette ed iperboli
- Trovare le rette tangenti a una ellisse
e a una iperbole
- Determinare le equazioni di ellissi e
iperboli traslate
- Risolvere particolari equazioni e
disequazioni mediante la
Risolvere particolari equazioni e
rappresentazione grafica di archi di
disequazioni
ellissi o di iperboli
Conoscere le funzioni goniometriche - Conoscere e rappresentare
e le loro principali proprietà
graficamente le funzioni seno,
coseno, tangente, cotangente e le
funzioni goniometriche inverse
- Calcolare le funzioni goniometriche di
angoli particolari e di angoli associati
Operare con le formule
- Applicare le formule di addizione,
goniometriche
sottrazione, duplicazione, bisezione,
parametriche, prostaferesi, Werner
Risolvere equazioni goniometriche - Risolvere equazioni goniometriche
elementari
- Risolvere equazioni lineari in seno e
coseno
- Risolvere equazioni omogenee di
secondo grado in seno e coseno
- Risolvere sistemi di equazioni
goniometriche
- Risolvere disequazioni goniometriche
- Risolvere sistemi di disequazioni
goniometriche
Risolvere disequazioni goniometriche
Programmazione per competenze del corso Matematica.Verde, Volume 3
Unità
didattica
La trigonometria
I numeri complessi e i
vettori
Competenze
Traguardi formativi
M6. Utilizzare il linguaggio e i metodi - Conoscere le relazioni fra lati e
propri della matematica per organizzare angoli di un triangolo rettangolo
e valutare adeguatamente informazioni
qualitative e quantitative
- Applicare i teoremi sui triangoli
rettangoli
M7. Utilizzare i concetti e i modelli delle scienze sperimentali per investigare
fenomeni sociali e naturali e per
interpretare i dati
M5. Utilizzare le strategie del pensiero razionale negli aspetti dialettici e
algoritmici per affrontare situazioni
problematiche, elaborando opportune
soluzioni
-
Indicatori
- Applicare il primo e il secondo
teorema sui triangoli rettangoli
- Risolvere un triangolo rettangolo
- Calcolare l’area di un triangolo e il
raggio della circonferenza circoscritta
- Applicare il teorema della corda
Risolvere un triangolo qualunque
- Applicare il teorema dei seni
- Applicare il teorema del coseno
- Applicare la trigonometria alla fisica e
Applicare la trigonometria
a contesti della realtà
Operare con i numeri complessi nelle - Operare con i numeri complessi in
varie forme di rappresentazione
forma algebrica
- Operare con i numeri complessi in
forma trigonometrica
- Operare con i numeri complessi in
forma esponenziale
- Calcolare la radice
n-esima di un numero complesso
- Interpretare i numeri complessi come
vettori
Rappresentare nel piano di Gauss i - Corrispondenza fra coordinate
numeri complessi
cartesiane e polari












