matrici (eserciz1)

ESERCIZI
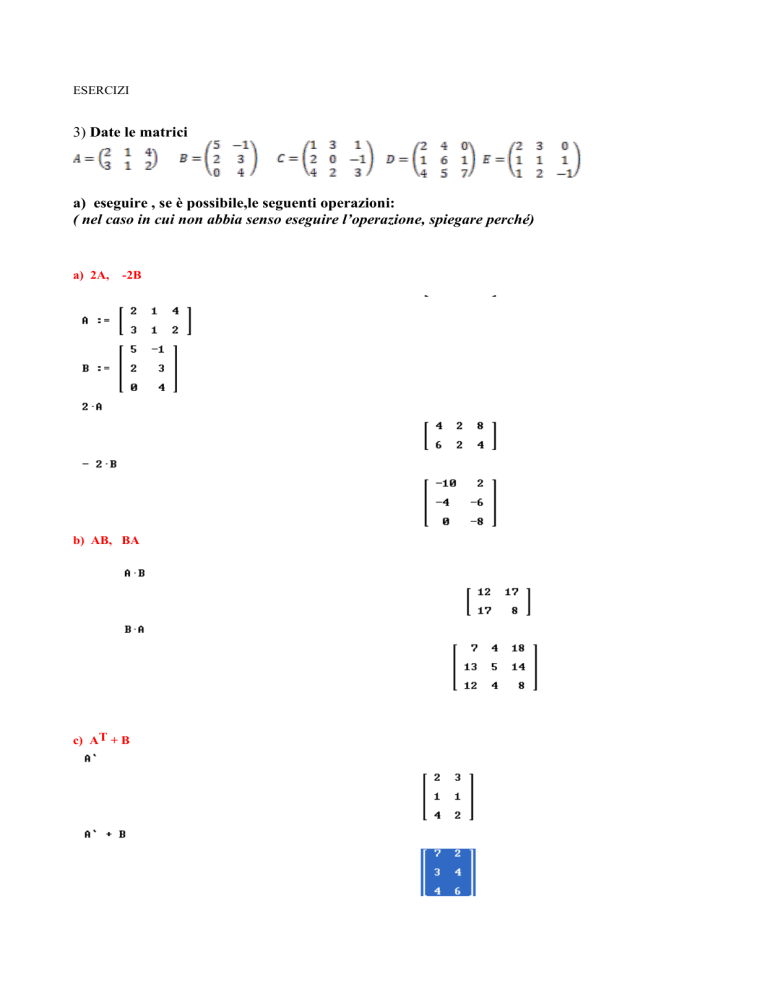
3) Date le matrici
a) eseguire , se è possibile,le seguenti operazioni:
( nel caso in cui non abbia senso eseguire l’operazione, spiegare perché)
a) 2A,
-2B
b) AB, BA
c) AT + B

C-2* E

A*C,
C*A impossibile
 A+B
impossibile
T

A +B




Det (A) impossibile
Det(C) =-24
Det (E)= 0


A-1 impossibile La matrice non è quadrata
D-1
E-1 impossibile Il determinante è nullo
2) Date le due matrici
Determinare una matrice X tale che
a) XA=B
b) A-X=B
X=A-B
3) Risolvere la seguente equazione
=4
4x2=4→ x=±1
4) Determinare il rango della matrice seguente, in dipendenza del valore di x
Il determinante della matrice , in funzione di x, è uguale a
(x+3)(x2-2x-3)
quindi si annulla per x= -3 x=-1 x=3
PERTANTO
Se x± -3 x≠-1 x≠3 il RANGO è 4
Se
x= -3
la matrice diventa
RANGO
3
Se x =-1 la matrice diuventa
RANGO 3
Se
x= 3
la matrice diventa
RANGO 3
5)Si stabilisca la relazione cui debbono soddisfare a e b (parametri reali con a  1 ) affinché
la matrice
a 1 b


1 1 a
1 a b


abbia rango 2.
Interpretando a e b come coordinate di un punto di un piano riferito ad un sistema di assi
cartesiani, si tracci il grafico della suddetta relazione
SOLUZIONE
Poiché a è diverso da 1, la matrice ha sicuramente un minore del seconro ordine diverso
da 0 :
pertanto se il suo determinante è nullo , il suo rango è 2.
Imponendo che il determinante sia nullo si trova l’equazione
-a3+2ab+a-2b=0
che può essere scritta nella forma
e corrisponde all’equzione di una parabola