ARITMETICA

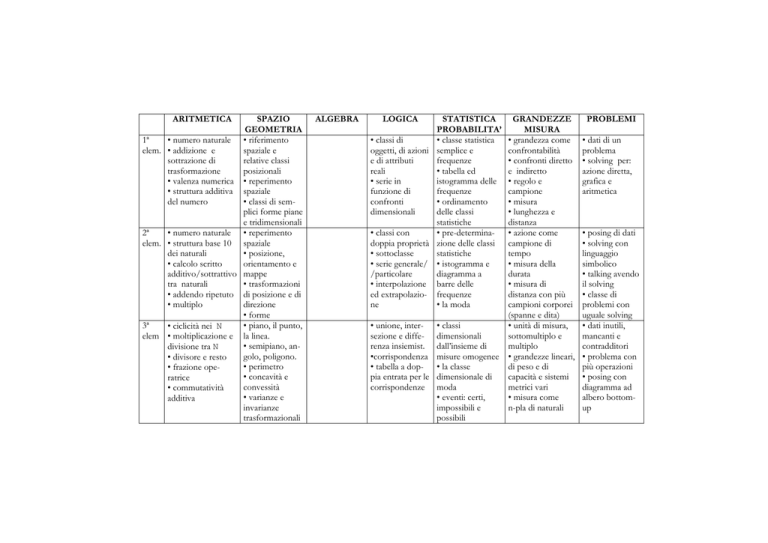
ARITMETICA
SPAZIO
GEOMETRIA
1ª
• numero naturale • riferimento
elem. • addizione e
spaziale e
sottrazione di
relative classi
trasformazione
posizionali
• valenza numerica • reperimento
• struttura additiva spaziale
del numero
• classi di semplici forme piane
e tridimensionali
2ª
• numero naturale • reperimento
elem. • struttura base 10 spaziale
dei naturali
• posizione,
• calcolo scritto
orientamento e
additivo/sottrattivo mappe
tra naturali
• trasformazioni
• addendo ripetuto di posizione e di
• multiplo
direzione
• forme
3ª
• piano, il punto,
• ciclicità nei N
elem • moltiplicazione e la linea.
• semipiano, andivisione tra N
golo, poligono.
• divisore e resto
• perimetro
• frazione ope• concavità e
ratrice
convessità
• commutatività
• varianze e
additiva
invarianze
trasformazionali
ALGEBRA
LOGICA
STATISTICA
PROBABILITA’
• classi di
• classe statistica
oggetti, di azioni semplice e
e di attributi
frequenze
reali
• tabella ed
• serie in
istogramma delle
funzione di
frequenze
confronti
• ordinamento
dimensionali
delle classi
statistiche
• classi con
• pre-determinadoppia proprietà zione delle classi
• sottoclasse
statistiche
• serie generale/ • istogramma e
/particolare
diagramma a
• interpolazione barre delle
ed extrapolazio- frequenze
ne
• la moda
GRANDEZZE
MISURA
• grandezza come
confrontabilità
• confronti diretto
e indiretto
• regolo e
campione
• misura
• lunghezza e
distanza
• azione come
campione di
tempo
• misura della
durata
• misura di
distanza con più
campioni corporei
(spanne e dita)
• unione, inter- • classi
• unità di misura,
sezione e diffe- dimensionali
sottomultiplo e
renza insiemist. dall’insieme di
multiplo
•corrispondenza misure omogenee • grandezze lineari,
• tabella a dop- • la classe
di peso e di
pia entrata per le dimensionale di
capacità e sistemi
corrispondenze moda
metrici vari
• eventi: certi,
• misura come
impossibili e
n-pla di naturali
possibili
PROBLEMI
• dati di un
problema
• solving per:
azione diretta,
grafica e
aritmetica
• posing di dati
• solving con
linguaggio
simbolico
• talking avendo
il solving
• classe di
problemi con
uguale solving
• dati inutili,
mancanti e
contradditori
• problema con
più operazioni
• posing con
diagramma ad
albero bottomup
ARITMETICA
4ª
• N: multiplo,
elem divisore e primo
• moltiplicazione
combinatoria
• decimali e loro
operazioni
• num. relativo (Z)
come
equidifferenze
• invariantiva nelle
differenze
• “zero” relativo
come uguaglianza.
5ª
• frazione come
elem rapporto
• invariantiva e
frazioni equivalenti
• frazione unitaria e
numero decimale
• percentuale
• numero relativo
come vettore sulla
rette delle ascisse
SPAZIO
GEOMETRIA
• angolo come
cambiamento di
direzione
• classificazioni
degli angoli
•perpendicolarità
e parallelismo
• altezza e
bisettrice
• classificazioni
dei quadrilateri e
dei triangoli
• isoperimetria
• equiestensione
• ortocentro e
baricentro dei
triangoli
• polig. regolare
• equiestensione
e calcolo aree
• ampiezza
• isometrie
euclidee
• piano e coordinate cartesiane
ALGEBRA
LOGICA
• elemento
algebrico
( N,op)
•“0” el. neutro
in ( N,+)
•“1” el. neutro
in ( N,x)
•“0” el. assorbente in ( N,x)
• relazione
aritmetica fra
insiemi numerici
(il doppio, la
metà, due in
più,…)
• piano cartesiano per le relazioni aritmetiche
• relazione d’ordine fra decimali
• divisori e multipli comuni di
due naturali
• proprietà
associativa
delle operazioni dirette
• proprietà
distributiva
della
moltiplicazione
rispetto alla
addizione
• ordine nei
numeri relativi
• ascisse e “0”
per riferimento
• equivalenze
linguistiche fra
tabelle, grafici e
piano cartesiano
STATISTICA
PROBABILITA’
• indagine dimensionale: ordinamento dei dati in
classi statistiche
• valore medio
(media artim.)
• scarto relativo
rispetto al dato
medio
• tricotomia:
certo, impossibile,
possibile
• quantificatori
probabilistici
GRANDEZZE
MISURA
• sistema metrico
decimale
•estensione
• area come
ricoprimento
• area del rettangolo come calcolo
• sistema metrico
centesimale
• ampiezza: quantità di rotazione.
• “ora” come unità
angolare
• distribuzione dei
dati e mediana
• valore percentuale delle classi
statistiche
• eventi possibili,
eventi favorevoli
• probabilità
matematica
• “grado” unità di
misura angolare
• sistema metrico
sessagesimale per il
tempo
• misura relativa
(temperatura,
altezza, … )
PROBLEMI
• terne dimensionali lordotara-netto e
ricavo-costoguadagno
• posing con
diagramma ad
albero topdown
• scomposizione
in
sottoproblemi
• diagrammi ad
albero e di flusso per il posing
• espressione
numerica del
solving
• scelta condizionale nei
diagrammi di
flusso
• testi dai
diagrammi del
posing/solving
ARITMETICA
1ª
med
2ª
med
• criteri di divisibilità dei N
• potenza e radice
• scomposizione in
fattori di un N
• mcm e MCD fra
numeri N
• confronto fra
frazioni
• somma e differenza fra frazioni e
fra num. relativi
•espressione
numerica
• num. razionali e
le operazioni aritm.
• decimale limitato,
periodico e le frazioni generatrici
• arrotondamento
• proprietà delle
potenze con esponente naturale >1
• moltiplicazione e
divisione nei
numeri relativi (Z)
• potenza nei Z
SPAZIO
GEOMETRIA
• relazione fra
angoli (consecutivi, adiacenti,
supplementari,..)
• rapporti metrici nei poligoni
reg., e nei triang.
emiequilateri
• simmetria, rotazione,
omotetia
• assi e centri di
simmetria nelle
figure
• circonferenza e
cerchio
• il rapporto 
• inscrivere e
circoscrivere
• teorema di
pitagora e sue
verifiche
• terne pitagoriche
• superfici (base
e laterale) dei
solidi semplici
ALGEBRA
STATISTICA
PROBABILITA’
• elementi
• relazione di un • scelta delle classi
statistiche
algebrici (N,+) insieme in se
(N,x) e (N,+,x) stesso: proprietà, • media aritmetica
antiproprietà e
e mediana
• l’elemento
• nessi linguistici
algebrico (Z,+) non-proprietà
• relazioni di
fra: tabelle, istoe gli elementi
parentela
grammi e aeroopposti.
• relazioni aritgrammi a torta,
• elementi
metiche (multi- • permutazione e
algebrici (A,)
plo di, diretta
combinazione:
riscontrabili
proporzionalità loro costruzioni
nella vita
• grafici carte• probabilità macomune
siani
tematica
• elementi opposti e inversi
in (Q,+), (Q,x)
e (Q,+ ,x)
• inesistenza
dell’inverso
dello “0”
• la proprietà
distributiva
• monomi e
espressioni
moltiplicative
• geometria e
monomi
LOGICA
•proporzionalità
diretta e inversa
• funzioni e loro grafico
cartesiano
• funzioni tipo
y=ax y=a/x nel
piano cartesiano
• proporzioni e
quarto incognito
nel piano cartes.
• campione statistico e la sua
rappresentatività
• inferenza
• permutazione e
combinazione:
criteri per
ottenerle
• combinazioni
con ripetizione
• misurazioni e
distribuzione
gaussiana
GRANDEZZE
MISURA
• prefissi per i
multipli e
sottomultipli di
una unità
• angolo e sistema
sessagesimale
• s.i. di misura
• proporzionalità
fra grandezze per
misure indirette
• stima e ordine di
grandezza
• approssimazione
nelle misurazioni
• misura approssimata di aree tramite: rapporti con
altre grandezze,
metodo stocastico
• misura derivata:
pressione, momento di una forza,…
• strumenti di
misura
• misurazione ed
errori
• propagazione
degli errori
PROBLEMI
• non equivocità nel problem
talking (dati
inutili mancanti
o contradditori)
• problem posing fatto con
simboli (dei
dati) e grafi
• solving come
svolgimento di
espressioni
tratte dal posing
• variabili e classi di problemi
• diagrammi con
le variabili
• l’incognita nel
posing (4° incognito)
• problemi non
deterministici
• verifica delle
soluzioni
3ª
med
• gli irrazionali
quadratici e la
trascendenza del 
• ricorsione
aritmietica per
l’approssimazione
di una radice
• ordinamento dei
numeri reali sulla
retta delle ascisse
• sviluppo piano
delle superfici
dei solidi
• i solidi più comuni e il loro
volume
• relazioni tra
rette e/o piani
nello spazio
• trasformazioni
isometriche
ricondotte alla
simmetria assiale
• l’incognita
nelle forme
proposizionali
• operazioni
inverse
• risoluzioni di
equazioni nel
piano
cartesiano
• risoluzioni di
equazioni con
sequenze di
op. inverse
•proporz. quadratica y = ax²
• logica dei circuiti delle classi,
e delle proposiz.
• gli operatori
logici and, or,
not, aut
• i quantificatori
esistenziale e
universale come
operatori logici
ripetuti
• eventi: possibili
e favorevoli
• probabilità:
matematica e
frequentista
• dalla probabilità
matematica a
quella soggettiva
• previsione
probabilistica
degli sviluppi di
una situazione
• l’incommensurabilità
• misura attendibile e vero valore
• distribuzione
gaussiana delle
misure di una
grandezza fisica
• volumi ed il
sistema metrico
millesimale
• grandezze derivate dai volumi
• posing di un
problema con le
equazioni
• valutazione e
eventuale inaccettabilità di
risoluzioni
• problemi con
diversi posing e
solving