Limite

A) LIMITE PER x TENDENTE AD UN VALORE FINITO
Sia f(x) una funzione reale di una variabile reale ,D il suo dominio e c un punto di accumulazione
del Dominio ( cioè tale che in ogni suo intorno comunque piccolo cadono infiniti punti di D)
1° caso: Limite finito per x che tende ad un valore finito
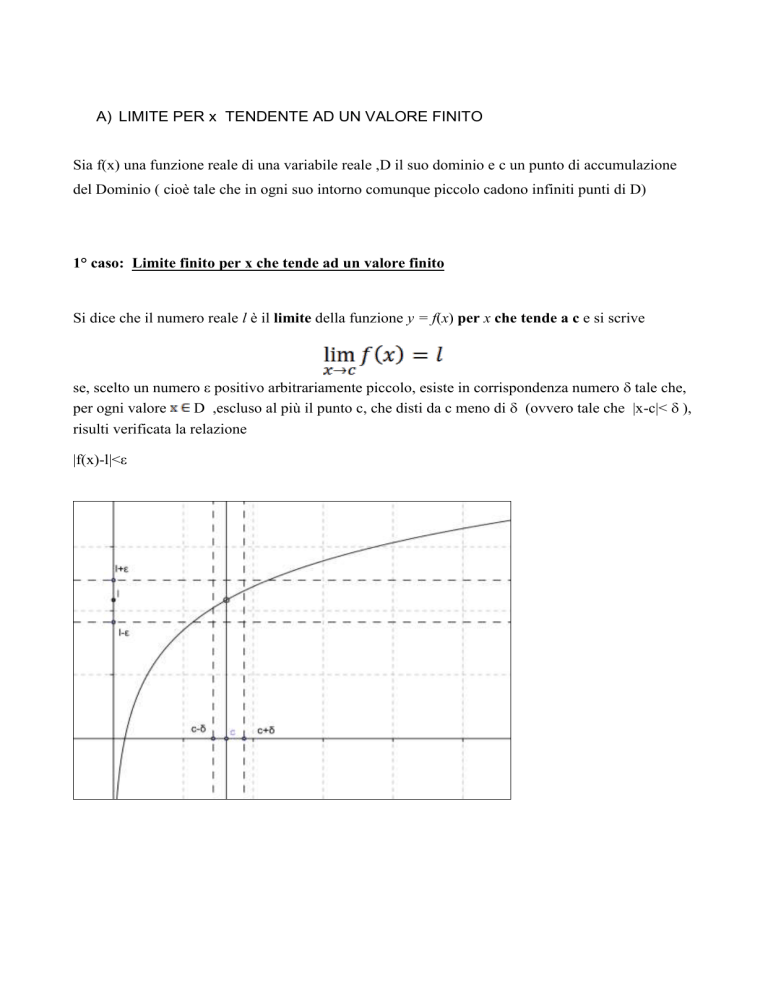
Si dice che il numero reale l è il limite della funzione y = f(x) per x che tende a c e si scrive
se, scelto un numero ε positivo arbitrariamente piccolo, esiste in corrispondenza numero  tale che,
per ogni valore
D ,escluso al più il punto c, che disti da c meno di  (ovvero tale che |x-c|<  ),
risulti verificata la relazione
|f(x)-l|<ε
2° caso: Limite infinito per x che tende ad un valore finito
Si dice che la funzione f(x) ha limite ∞ per x che tende a c e si scrive
se, scelto un numero M positivo arbitrariamente grande, esiste in corrispondenza un numero
 tale che, per ogni valore
che |x-c|< ,
D , escluso al più il punto c, che disti da c meno di ,( ovvero tale
risulti verificata la relazione
|f(x)|>M
Se in particolare valgono le relazioni
f(x)> M
o
f(x)<-M
Si dice che la funzione tende, rispettivamente, a +∞ o a -∞ e si scrive
B)LIMITE PER x TENDENTE AD INFINTO
1° caso: Limite finito per x che tende ad infinito
Sia y=f(x) una funzione che abbia come dominio un insieme D illimitato, si dice f(x) ha per limite l
al tendere di x all’infinito e si scrive
se, scelto un numero ε positivo arbitrariamente piccolo, esiste in corrispondenza numero
positivotale che, per ogni valore
D tale che |x|>N risulti verificata la relazione
|f(x)-l|<ε
2° caso: Limite infinito per x che tende ad infinito
Sia y=f(x) una funzione che abbia come dominio un insieme D illimitato, si dice f(x) ha per limite
infinito al tendere di x all’infinito e si scrive
se, scelto un numero M positivo arbitrariamente grande ,esiste in corrispondenza un numero
positivotale che, per ogni valore
D tale che |x|>N, risulti verificata la relazione
|f(x)|>M
Osserviamo però che le precedenti definizioni non permettono,operativamente,di
determinare il limite di una funzione, ma piuttosto di dimostrare che un valore congetturato è
effettivamente il limite della funzione
Per determinare delle regole di calcolo dobbiamo fissare bene le proprietà dei limiti, mediante i
teoremi fondamentali.
Teorema dell'unicita' del limite
Teorema della permanenza del segno
Teorema del confronto ( detto dei "carabinieri" )
Operazioni sui limiti
Teorema dell'unicita' del limite
Se una funzione f(x) ammette limite per x tendente a c, questo limite è unico
In pratica le relazioni
Sono a due a due incompatibili, cioè una sola di esse può essere vera
Teorema della permanenza del segno
Il teorema afferma che se una funzione f(x) , per x tendente a c tende ad un limite finito l≠0, esiste
almeno un intorno del punto c per tutti i punti del quale (escluso al più il punto c) la funzione ha lo
stesso segno del suo limite.
Teorema del confronto ( detto dei "carabinieri" )
Consideriamo tre funzioni f(x), g(x) e h(x) e supponiamo che valgano le seguenti ipotesi
 Tutte e tre siano definite nello stesso intervallo, eccettuato al più un punto c di esso
 In ogni punto di tale intervallo sia f(x)≤h(x)≤g(x)
 Esista il limite delle due funzioni f(x) e g(x) e sia
Allora esiste anche il limite di h(x) ed è
La notazione scherzosa di teorema dei carabinieri si riferisce all’osservazione che la prima e la
terza funzione fanno da <<carabinieri >>e prendono in mezzo la seconda per portarla in
<<prigione>> nel limite
Operazioni sui limiti



limite di una somma o di una differenza
limite di un prodotto
limite di un quoziente
Se abbiamo due funzioni y=f(x)
e se
y=g(x)
Allora
Limite di una somma o di una differenza di funzioni
Limite di un prodotto
Limite di un quoziente