Statistica

Definizioni di Statistica e Calcolo delle Probabilità
Spazio Campione [S]:l'insieme dei punti che rappresentano i possibili risultati di un esperimento.
 Spazio Campione Discreto: spazio campione che consiste in un numero finito o in una
successione infinita di punti.
 Spazio Campione Continuo: spazio campione che consiste in uno o più intervalli di punti.
Evento: sottoinsieme di uno spazio campione [può coincidere con esso o essere vuoto]. Un evento e
lo spazio campione possono essere rappresentati tramite i diagrammi di Venn.
 Eventi Disgiunti: due eventi A1 e A2 che non hanno punti in comune. [P{A1UA2} = P{A1} + P{A2}]
 Eventi Indipendenti: due eventi t.c. P{A2|A1} = P{A2} e P{A1} ∙ P{A2} >0 allora x la regola
della moltiplicazione:P{A1∩ A2} = P{A1} ∙ P{A2}
Unione di A e B [A U B]: l'insieme dei punti che consiste di tutti i punti che appartengono ad A o a
B o sia ad A che a B.
Intersezione di A e B [A
sia ad A che a B.
∩
B]: l'insieme dei punti che consiste di tutti i punti che appartengono
Complementare di A [Ā]: l'insieme dei punti che consiste di tutti i punti che non appartengono ad
A.
Probabilità da A [P{A}]: modello per la frequenza del verificarsi di un certo risultato in ripetute
esecuzioni dell'esperimento.
Assiomi della Probabilità:
 0 ≤ P{A} ≥ 1
 P{S} = 1
 P{A1 U A2 U ...} = P{A1} + P{A2} + ...
(per ogni successione finita o infinita di eventi disgiunti A1, A2,...)
Regola di Addizione delle Probabilità: P{A1UA2} = P{A1} + P{A2} - P{A1∩ A2}
Probabilità di un Evento:
 P{A} = ∑A pi
(con diversa probabilità per ogni punto)
 P{A} = N(A) / n
(con uguale probabilità per ogni punto)
Probabilità Condizionata: la probabilità che l'evento A2 si verifichi sotto la condizione che l'evento
A1 sia certo di verificarsi. P{A2|A1} = P{A1∩ A2} / P{A1}
Regola della Moltiplicazione delle Probabilità:
P { A1∩ A2 }= P { A1 }⋅ P { A2 | A1 }
Formula di Bayes:formula per calcolare la probabilità delle cause [prob che Hi sia la causa del
verificarsi dell'evento A]. H1, H2, .. , Hn sono eventi mutualmente esclusivi con P{Hi}=pi, con pi>0.
Gli eventi Hi costituiscono una partizione dello spazio campione: essi rappresentano le n possibili
cause di un risultato sperimentale.
P { H i | A}=
P { H i }⋅ P { A| H i }
n
∑ P { H j }⋅ P { A| H j }
j= 1
per i=1..n e j=1..n
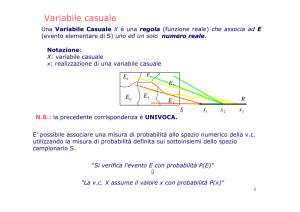
Variabili Casuali o Aleatorie: una variabile casuale X è una funzione a valori reali definita su di uno
spazio campione associato ad un esperimento fisico il cui risultato è incerto ovvero si dice che
dipende dal caso.

Variabili Casuali Discrete: una variabile casuale definita su di un spazio campione discreto
che può assumere soltanto un numero finito o una successione infinita di valori.
-
Se x è uno specifico valore della variabile casuale discreta X, la probabilità che X assuma il valore x è
P { X = x }=
∑
X= x
.
P { X ∈ R }= ∑ f x
.
Variabili Casuali Continue: una variabile definita su di uno spazio campione continuo.

pi
Se R è un insieme di punti, la probabilità che X assuma valori di R è
x ∈R
Funzione di Probabilità Congiunta o densità di probabilità congiunta: siano X e Y due variabili
casuali discrete, allora la funzione f definita da
probabilità congiunta se:
f x,y
1.
2.
→
∑∑
X
f x , y := P { X = x;Y=y} viene chiamata funzione di
0
f x, y =1
Y
Variabili Casuali Indipendenti: due variabili che sono senza rapporti in senso probabilistico.
Le variabili casuali X,Y, la cui funzione di densità congiuta è f x , y e le cui funzioni di
densità individuali g(x), h(x), sono indipendenti se:
f x , y = g x h x per ogni x,y.
Distribuzioni Marginali:consideriamo un esperimento in cui A1 rappresenta l'evento che una
variabile casuale X assuma il valore x e A2 l'evento che una seconda variabile casuale Y assuma il
valore y.
P { A1∩ A2 }= P { A1 }⋅ P { A2 | A1 }
f x, y = f x ⋅ f y|x
f y| x da la probabilità condizionata che Y assuma il valore y quando X ha per valore fissato il
valore x. La somma su tutti i possibili valori y deve essere uguale a 1.
∑
f x, y = f x ⋅
∑
y
f y|x = f x
f x =∑ f x,y
y
y
1
essa è detta Funzione di Densità Marginale (funzione di densità di X). Quella di Y, g(x) è fatta con
la sommatoria da x.
Distribuzioni Condizionate: la distribuzione di probabilità della variabile Y quando viene
mantenuto fisso il valore di X è f
Quella con Y fisso è
f x| y =
y| x =
f x,y
g y
f x,y
f x
con g y
con f x
0 [Funzione di Densità Condizionata].
0.
Funzione di Densità di Probabilità di una:
 Variabile Casuale Discreta: sia X una variabile casuale discreta, allora la funzione f definita
da f x := P { X = x} viene chiamata la funzione di densità di probabilità della variabile X se:
f x
1.
∑

0
f x =1
x
2.
Variabile Casuale Continua:la funzione di densità di probabilità di una variabile casuale
continua X è una funzione f che possiede le seguenti proprietà:
f x
1.
0
−∞
∫
f x dx= 1= P {− ∞ x
∞}
∞
2.
b
∫
3.
f x dx= P {a x b }
con a ,b ∈ X ,a b
a
Frequenza: il rapporto fra il numero di volte che si presenta uno specifico valore della variabile X e
il numero totale di valori osservati.
Istogramma: grafico in cui si usano delle aree per rappresentare le frequenze.
x
Funzione di Distribuzione per una Variabile Continua X: F x = P { X
x }= ∫ f t dt
−∞
Funzione di Densità Congiunta Continua: una funzione di densità di due variabili casuali
continue X e Y è una funzione f t.c.:
1.
f x,y
∫ ∫
2.
3.
0
−∞ − ∞
∞
∫∫
R
f x , y dx dy= 1
∞
f x , y dx dy= P { X ,Y ∈ R}
Distribuzione Binomiale: la probabilità di ottenere x successi in n esecuzioni indipendenti di un
esperimento di tipo ripetitivo, in cui p è la probabilità del verificarsi di un evento e q=1-p è quella
che esso non si verifichi, definisce
f x =
n!
x
n− x
⋅p⋅q
x ! n− x !
x
[Funzione di Densità Binomiale]
n− x
x
n− x
Essa si ricava dalla moltiplicazione di p⋅ p⋅ ...⋅ p⋅ q⋅ q⋅ ...⋅ q = p ⋅ q
[probabilità di avere x successi seguiti da
n-x insuccessi, data dalla formula degli eventi indipendenti] per il numero di ordini possibili [cioè il numero di
permutazioni con n oggetti di cui x sono fra loro uguali(p) ed n-x sono anch'esse fra loro uguali (q)] che è
n!
x! n− x !
. Per ottenere la probabilità è necessario moltiplicare questo termine per
p x⋅ q n− x
.
Approssimazioni della Distribuzione Binomiale:
Distribuzione di Poisson: f x =
e− μ μ x
x!
n
∞ e p
0
con la media μ= n⋅ p fissa n 100 & p 0,05
gli eventi che si distribuiscono in qualsiasi regione dello spazio di dimensione fissata seguirà una distribuzione di Poisson.
Processo di Poisson: un esperimento in cui le osservazioni si susseguono in intervalli successivi di tempo o di spazio così che
gli eventi possiedano una distribuzione di Poisson.
1 x− μ
σ
−
1
1 x− a
f x =
e 2
Distribuzione Normale o− Gaussiana:
2
b
σ 2π
f x = c⋅ e
2
2
n
∞ e ∀ p
np 5 con p 1/ 2
o
nq 5 con p 1/2
La cui forma generale è
Graficamente la funzione è simmetrica, ha un punto di massimo in x=μ [vi si annulla la derivata prima] e due punti di
flesso in x=μ±σ [vi si annulla la derivata seconda]. La curva ha concavità verso il basso nell'intervallo [μ-σ , μ+σ] e verso
l'alto esternamente a questo intervallo. La probabilità che una variabile normale x cada nell'intervallo [μ-σ , μ+σ] è circa 68%
x− μ
La distribuzione può essere anche scritta in funzione di z tramite l'unita di misura z= σ [unità standard], cioè con μ=0 e
z2
−
1
2 .
σ=1, e viene detta distribuzione normale in unità standard o standardizzata, e si scrive:
f x =
2π
e
Se in n esecuzioni indipendenti di un esperimento la variabile X rappresenta il numero di successi di un evento per cui p è la
probabilità di successo in una singola esecuzione, allora la variabile
X − np
npq ha una distribuzione che tende alla distribuzione
normale con μ=0 e σ=1 quando n→∞.
Distribuzione Rettangolare o Uniforme: distribuzione costante in un
intervallo finito [a,b] ed è uguale a zero altrove.
{
1
, a x b
f x = b− a
0 , altrove
}
Distribuzione Gamma: essa comprende due parametri α>0 e β>0
{ }
{ }
− x
x α− 1⋅ e β
, x 0
f x = βα Г α
0
, x 0
Г(α) rappresenta il valore della funzione gamma nel punto α. Questa
∞
α− 1 − x
funzione è definita da: Г α = ∫ x ⋅ e dx . Г α 1 = α⋅ Г α = α!
0
Distribuzione Esponenziale: caso particolare della distribuzione gamma, con α=1
−
e
f x =
x
β
β
0
, x 0
∞
−x
−x ∞
con Г 1 = ∫ e dx = − e ] 0 = 1
0
, x 0
Distribuzione Chi-Quadrato(Χ2): caso particolare della distribuzione gamma, con β=2 e α=ν/2
{
ν− 1
2
−x
2
⋅e
f x = 2 Г ν
2
0
x
ν
2
, x 0
, x 0
}
ν = (ni) indica i gradi di libertà
Valore Atteso o Media di una :
 Variabile Casuale Discreta X: le probabilità che X assuma uno dei valori x1, x2, ..., xk sono
rispettivamente f(x1), f(x2), ..., f(xk). Il valore atteso della funzione g(X) della variabile
k
casuale discreta X è E [ g X ]= ∑ g x i ⋅ f x i .
i= 1

Variabile Casuale Casuale X: Il valore atteso della funzione g(X) della variabile casuale
∞
continua X è E [ g X ]=
∫
−∞
g x ⋅ f x dx .
Momenti:i momenti di una distribuzione aiutano a descrivere la distribuzione quando la funzione di
densità f non è disponibile. Essi sono casi particolari del valore atteso.
 Momenti di una Distribuzione di una Variabile Casuale Discreta X:
∞
f
- Momento d'ordine k dall'origine, la cui densità è
,è
μ ' k = E [ X ]= ∑ x ki ⋅ f x i
k
i= 1
∞
- Momento d'ordine k dalla media , la cui densità è
f
,è
μk = E [ X − μ ]= ∑ x i− μ k⋅ f x i
k
i =1

Momenti di una Distribuzione Binomiale:
n
- Momento del primo ordine k dall'origine è
n
μ= ∑
x= 1
x= 0
n
n− 1 !
n!
⋅ p x⋅ q n− x = n⋅ p⋅ ∑
⋅ p x− 1⋅ q n− x
x− 1 ! n− x !
x−
1
!
n−
x
!
x= 1
n
- Momento del secondo ordine k dall'origine è
μ '2=
∑ x 2⋅ x!
x= 0
n
x]
x= 0
n!
⋅ p x⋅ q n− x
n− x !
n!
n!
⋅ p x⋅ q n− x = ∑ x x− 1
⋅ p x⋅ qn− x μ
x! n− x !
x!
n−
x
!
x= 0
n
μ '2= n n− 1 p2 ∑
x= 2
n− 2 !
⋅ p z⋅ qn− 2− x
z ! n− 2− x !
μ'2= n n− 1 p2 np
con z= x− 2
f
,è
f
,è
μ'k =
∫
x k f x dx
−∞
∞
μk = ∫
x− μ
Momenti di una Distribuzione Normale o Gaussiana: μ2= b

1
k
k
Momenti di una Distribuzione Gamma: μ' k = E [ X ]= βα Г α ⋅ ∫ x
0
β k α− 1⋅ β
⋅
α
β⋅Г α
∫
∞
t
k α− 1
−t
⋅ e dt =
0
k
β Г k α
Г α
'
k
f x dx
−∞

2
∞
α− 1
⋅e
−
x
β
dx
con t=x/β e dx=βdt
k
μ k= β k α− 1 ⋅ k α− 2 ⋅ ... ⋅ ...⋅ α
con Г k α = k α− 1 ⋅ k α− 2 ⋅ ... ⋅ ...⋅ αГ α
Г k α

x
∞
- Momento d'ordine k dalla media , la cui densità è

con x 2 = x x− 1
Momenti di una Distribuzione di Poisson: μ= n⋅ p
Momenti di una Distribuzione di una Variabile Casuale Continua X:
- Momento d'ordine k dall'origine, la cui densità è
μ' k =
μ= n⋅ p
n
μ '2= ∑ [ x x− 1


n!
⋅ p x⋅ qn− x
x! n− x !
μ= E [ X ]= ∑ x⋅
da cui
μ= βα
μ '2 = β 2 1 α ⋅ α
Momenti di una Distribuzione Esponenziale: μ= β
Momenti di una Distribuzione Chi-Quadrato: μ= ν
Il momento del primo ordine dall'origine μ ' 1 = μ si usa per determinare dove la distribuzione è
centrata. Il momento del secondo ordine della media μ 2= σ [Varianza della Distribuzione] si usa
per determinare il grado di concentrazione della distribuzione attorno alla media μ.
σ viene chiamato Scarto Quadratico Medio o Deviazione Standard.
2
Varianza di una:
 Variabile Casuale Discreta:
μ'2
∞
μ
∞
σ 2= ∑ x i− μ 2⋅ f x i = ∑ x 2i⋅ f x i − 2μ⋅
i=1
i= 1

1
∞
∑ x i⋅ f
∞
∑
μ2⋅
xi
i= 1
σ 2= μ'2− μ2
i= 1
Distribuzione Binomiale: σ = μ2− μ
2
f x i = μ'2− 2μμ μ 2
'
σ= npq
2
2
σ = lim npq= lim μq= lim μ 1− p = μ

Distribuzione di Poisson:

2
'
2
Distribuzione Gamma: σ = μ2− μ

Distribuzione Esponenziale: σ = β

Distribuzione Chi-Quadrato: σ = 2ν
∞
n
2
∞
n
∞
n
σ 2= αβ 2
2
2
Funzione Generatrice dei Momenti della:
 Variabile Casuale Discreta X, la cui densità è f
∞
ΘX
Θx
,vale: M x Θ = E [e ]= ∑ e ⋅ f x i dove Θ serve sono per determinare i momenti.
i
i= 1
Sviluppiamo e
Θxi
in serie di potenze e sommiamo temine a termine ricavando
k
Θ ' Θ2 ' Θ 3 '
Θ
Mx Θ =1
μ1
μ2
μ 3 ... con
1!
2!
3!
k ! coefficiente del momento d'ordine k dall'origine.
Per generare un momento in particolare si deve derivare MX(Θ) rispetto a Θ=0 e viene
μ ' k=
M 'X
dove per k = 1

Θ ]Θ= 0=
μ'1
∣
dk M x Θ
dΘ k
, k= 2
∣
M 'X'
Θ= 0
Θ ]Θ= 0= μ '2 , ecc..
Variabile Casuale Continua X, la cui densità è f
,vale:
M x Θ = E [e
ΘX
∞
]= ∑ e Θx ⋅ f x i
i
dove Θ serve sono per determinare i momenti.
i= 1
Θxi
Sviluppiamo e in serie di potenze e sommiamo temine a termine ricavando si scopre che la
MX(Θ) generai i momenti come l'analoga per le variabili discrete.
Variabile Normale o Gaussiana: M x Θ = e

μΘ 1 σ 2Θ 2
2
Forma Generalizzata: Per generare i momenti di una funzione g(X) si deve
∞
sostituire e
Θx
con e
Θg x
nella MX(Θ) ottendendo: M g
x
Θ = E[e Θ g x ]= ∫ eΘ g x ⋅ f x dx .
−∞
Proprietà: sia c una costante allora
1.
M c⋅ g
2.
Mg x
Θ = M g x c⋅ Θ
x
c
Θ = e Θ⋅ c M g
x
Θ
Popolazione: la totalità dei possibili risultati sperimentali.
Campione della Popolazione: un insieme di dati ottenuti eseguendo l'esperimento un certo
numero di volte.
Inferenza Statistica: consiste nel costruire un modello e trarre delle conclusioni su di una
popolazione, servendosi di un campione estratto della popolazione stessa.
Marchio o Centro di Classe: ai dati che cadono in un certo intervallo di classe viene assegnato il
valore corrispondente al punto di mezzo dell'intervallo.
Classificazione: ha lo scopo di osservare geometricamente la natura della distribuzione empirica.
Momenti di una Distribuzione Empirica:
valori osservati di un campione di dimensione n della variabile casuale X
n

1
k
Momento d'ordine k dall'origine: m' k = ⋅ ∑ x i
n i= 1
con
m'1= x
Media del Campione che da il centro di gravità di una distribuzione empirica.
n

[Momenti del campione]
1
k
Momento d'ordine k dalla media: mk= ⋅ ∑ x i− x
n i= 1
2
'
−2
con m2 = s = m2− x
Varianza del Campione e s lo Scarto Quadratico Medio o Deviazione Standard del
Campione.
Momenti di una Distribuzione Classificata: se i valori di osservazione sono stati classificati in
una tabella di frequenza, con xi l'i-esimo marchio di classe, fi la frequenza assoluta di xi e Nc il
numero degli intervalli di classe, allora le formule della distribuzione empirica si approssimano a:
n
1
k
 Momento d'ordine k dall'origine: m' k = ⋅ ∑ x i ⋅ f i
n i= 1
n
1
k
 Momento d'ordine k dalla media: mk= ⋅ ∑ x i− x ⋅ f i
n i= 1
Stime di Parametri:


Stima Puntuale: un numero ottenuto da calcoli fatti sui valori osservati della variabile
casuale che serve come approssimazione del valore vero del parametro.
Stima per Intervallo: un intervallo determinato da due numeri ottenuti da calcoli fatti su
valori osservati dalla variabile casuale che dovrebbe contenere il vero valore del parametro.
Metodo dei Momenti: se un parametro di funzione di densità è un momento della distribuzione,
allora la sua stima sarà il corrispondente momento campione. Se una distribuzione ha 2 parametri
incogniti e nessuno fosse il momento della distribuzione, i parametri possono ancora essere stimati
calcolando il momento del primo e del secondo ordine della distribuzione [che saranno funzioni dei
2
parametri] uguagliandole rispettivamente a x e a s .
Esempio: due parametri α e β, che non sono momenti della densità γ,
devono essere stimati. Si sa che
μ= βα e che σ 2= αβ 2 allora
{
βα= x
2
2
αβ = s
2
x
2
s
2
s
β=
x
α=
}
Statistica Descrittiva:
la statistica è la scienza che studia i fenomeni collettivi, cioè un qualsiasi
fatto, avvenimento o situazione costituito da un numero sufficientemente grande di fenomeni singoli
tra loro simili.
Indagine Statistica: analisi di un fenomeno collettivo che consiste nell'analizzare come una
popolazione statistica si distribuisce rispetto ad una certa variabile statistica. Essa produce una serie
di informazioni [Dati Statistici] che permettono di comprendere meglio il fenomeno.
Essa si articola in:
1. Rilevazione dei dati.
2. Elaborazione dei dati.
3. Presentazione dei dati.
4. Interpretazione dei dati.
Popolazione Statistica: insieme degli elementi su cui si effettua l'indagine.
Unità Statistica: ciascuno degli elementi che fanno parte di una popolazione statistica.
Variabili Statistiche: una o più caratteristiche per cui una unità statistica differisce dall'altra.
Rispetto ad una di esse che si effettua l'indagine. Vi sono variabili:
- Quantitative o Numeriche: che posso essere espresse con numeri.
- Qualitative: che non possono essere espresse con numeri.
Rilevazione dei dati:
1. Rilevazione Completa: estesa a tutte le unità statistiche della popolazione in esame.
2. Rilevazione per Campione: estesa solo ad una parte della popolazione statistica [meno
precisa e attendibile]. Il campionamento può essere
Campionamento non Probabilistico:di ogni elemento della popolazione non è nota la
probabilità che venga scelto.
Campionamento Probabilistico: il contrario. Ce ne sono vari: campioni aleatori,
campioni a più stadi, campioni stratificati, campioni sistematici, campioni a gruppi.
Metodi di rilevazione dei dati nelle indagini statistiche:
Intervista,
Questionario,
Inchiesta telefonica,
Consultazione archivi,
Consultazione di pubblicazioni specializzate.
Elaborazione, Presentazione e Interpretazione:
1. Tabulazione: Ottenuti i dati grezzi dalla rilevazione essi possono essere inizialmente riportati
in una matrice, poi possono essere organizzati in qualche forma che gli dia un ordine, si può
allora pensare di organizzarli in classi. Rango o Campo di Variazione: la lunghezza
dell'intervallo [a,b] in cui i dati sono contenuti: r=b-a.
2. Classificazione:
Tre criteri di classificazione.
Criterio 1: il numero delle classi deve rendere chiara la natura di tutta la distribuzione.
Esso è compreso tra 6 e 20. Il numero ottimale di classi è Nc=[1+1,1443·ln N] dove
[α]
rappresenta l'intero più vicino ad α ed N è il numero dei dati osservati [Sturges].
Criterio 2: le classi devono avere la stessa ampiezza h=r/Nc [r= rango dell'insieme dati
osservati.]
-
Criterio 3: l'ampiezza dell'intervallo deve essere un numero tale da individuare il punto di
mezzo, inoltre gli estremi di ogni intervallo di classe devono essere presi mezza unità
oltre l'accuratezza di misura affinché nessun dato cada sugli estremi.
Altri Indici Statistici:
- Funzione di Frequenza Assoluta [φ(x)]: ad ogni classe associa il numero di elementi della
classe.
- Funzione di Frequenza Relativa: φr(x) = φ(x) / N
[N=numero totale elementi]
- Funzione di Frequenza Cumulativa: φc(x) = φ(xn) + φ(xn-1) + ... + φ(x0)
- Funzione di Frequenza Cumulativa Relativa: φcr(x)=φc(x) / N
3. Rappresentazione Grafica:
Istogramma;
Grafico a Segmenti;
Poligono di frequenza assoluta, relativa, cumulativa e cumulativa relativa;
Ideogramma;
Areogramma.
4. Calcolo delle misure caratterizzanti:
Misure di tendenza centrale [danno l'idea di dove si collochi e quanto sia concentrata la
distribuzione]:
Media:fa la media dei dati. Tende a livellare tutti i dati e a non far risaltare le
grosse
differenze che possono esserci tra essi.
n
1
x= ⋅ ∑ x i
n i= 1
[Media Aritmetica delle Osservazioni]
- Media Geometrica:
- Media Armonica:
x g = n x 1⋅ x 2⋅ ...⋅ x n = x1⋅ x 2⋅ ...⋅ x n
xa=
n
1 1
1
⋅ ⋅ ...⋅
x1 x2
xn
Mediana:tiene
successione dei dati e non è quindi
piccoli.
x med =
1
x x
2 n2
n
1
2
1
n
con n pari
Nota: Se i valori sono tutti positivi si ha
xa x g x ,
conto solo del dato centrale della
influenzata né dai valori più grandi né da quelli più
x med = x n
1
con n dispari
2
Se i dati sono raggruppati per classi, prima individuare la classe mediana[classe dove
è situata la mediana], poi individuare la mediana con:
x med = λ m
n
− φ x m− 1
2
h⋅
φ xm
λm estremo inferiore della classe mediana,
h ampiezza delle classi,
xm punto di mezzo della classe mediana.
Moda: il dato che si ripete con maggior frequenza. Utile nel caso di dati non
numerici.
Se i dati sono raggruppati in classi, va prima determinata la classe modale [classe in
cui si trova la moda] e poi va calcolata la moda con:
x mod = λ j h⋅
| γ x j − γ x j− 1 |
| γ x j − γ x j−1 | | γ x j 1 − γ x j |
λj estremo inferiore della classe
Distribuzione Normale di Dati: il
caso in cui la distribuzione è
simmetrica rispetto un certo valore, allora media, mediana e moda coincidono oppure
hanno valori molto simili tra di loro. Il grafico ha una forma a campana, rappresentata da
una gaussiana.
Se i tre valori sono diversi, allora:
- Coda a Destra: Moda-Mediana-Media
- Coda a Sinistra: Media-Mediana-Moda
Per distribuzioni unimodali moderatamente asimmetriche vale x− x mod = 3 x− x med
-
Misure di dispersione:
mod
-
Scarto Quadratico Medio o Deviazione Standard
Varianza
Rango