4 - francescopoli.net

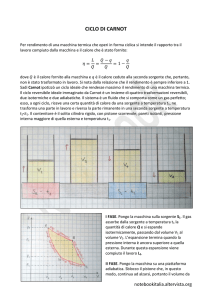
4. Il teorema di Carnot
Abbiamo calcolato il rendimento del motore di Carnot nel caso in cui a compiere il ciclo di due
isoterme e due adiabatiche sia un gas perfetto, ottenendo:
T
 1 F
TC
Vogliamo ora dimostrare quello che va sotto il nome di teorema di Carnot, vale a dire: in primo
luogo che se a compiere il ciclo di Carnot è una qualunque altra sostanza, un qualsivoglia gas reale,
oppure un miscuglio gassoso, o un miscuglio di gas e vapore, o altro ancora, il rendimento rimane
lo stesso. Ma, soprattutto, evidenziare in maniera rigorosa quello che finora è stato solo intutivo:
che nessun motore, reversibile od irreversibile che sia, può avere un rendimento superiore a quello
del motore di Carnot:
TEOREMA DI CARNOT:
IL MASSIMO RENDIMENTO FRA TUTTI
I CICLI TERMICI CHE OPERANO FRA LA STESSA
TEMPERATURA MINIMA TMIN E MASSIMA TMAX COMPETE AI CICLI REVERSIBILI CHE SCAMBIANO
CALORE SOLO CON DUE SORGENTI, UNA A TMIN ED UNA A TMAX.
ESSI SONO DETTI CICLI DI CARNOT, ED IL LORO RENDIMENTO È SEMPRE 1 
Tmin
Tmax
QUALUNQUE SIA
LA NATURA DEL SISTEMA FISICO CHE COMPIE IL CICLO.
Consideriamo prima la seconda parte del teorema e procediamo per assurdo supponendo di avere
oltre alla macchina di Carnot CA a gas perfetto, della quale si è calcolato il rendimento, una seconda
macchina di Carnot CB che operi fra le stesse due sorgenti TC e TF, scambiando calore solo con
esse. Supponiamo di tararle in modo che entrambe in ciascun ciclo compiano uno stesso lavoro W.
La CA lo farà assorbendo una quantità di calore QAC dalla sorgente calda e cedendo una quantità di
calore QAF alla sorgente fredda, mentre la CB assorbendo QBC e cedendo QBF rispettivamente.
Vogliamo mostrare ora che hanno entrambe lo stesso rendimento, cioè che A = B.
TC
TC
QAC
QBC
CB
CA
CB
CA
W
W
W
QAF
QBC
QAC
QBF
TF
Fig. 4.1: Macchine di Carnot
QBF
QAF
TF
Fig. 4.2: Macchine di Carnot combinate
Supponiamo per assurdo che sia B > A. Dalla definizione di rendimento  = W/QC abbiamo che,
essendo state le macchine tarate per compiere lo stesso lavoro W:
W
W

 QAC  QBC
| QBC | | QAC |
Dove il significato dei simboli è illustrato in figura 4.1. Abbiamo usato i moduli, pur essendo le
quantità calde sicuramente positive, in quanto è il calore che l’ambiente fornisce alle macchine,
perché nel seguito sarà utile che i segni dei calori compaiano esplicitamente.
Il lavoro W compiuto da entrambe le macchine è lo stesso perché così le abbiamo tarate, quindi, dal
primo principio:
B   A

W = |QAC| - |QAF| = |QBC| - |QBF|
Ed essendo, come si è visto, QAC  QBC , portando a primo membro |QBC| e a secondo |QAF|
risulta che:
|QAC| - |QBC| = |QAF| - |QBF| > 0
Ora, essendo la macchina CA reversibile la si potrà far funzionare al contrario. Un motore che
funziona al contrario assorbe calore dalla sorgente fredda, subisce lavoro, e cede calore alla
sorgente calda, è diventato una macchina frigorifera. La CA in figura 4.2 riceve calore QAF dalla
sorgente a TF , subisce il lavoro W e cede alla sorgente calda QAC.
Se ora però il lavoro W lo prendo proprio da CB, il dispositivo combinato CA+CB costituisce una
macchina che senza subire lavoro dall’esterno scambia calore sia con la sorgente fredda che con
quella calda. Più precisamente, con la sorgente fredda scambia la quantità di calore:
|QAF| - |QBF|
e tale quantità è sicuramente positiva se B   A , come si è mostrato sopra, quindi il calore |QAF|
che esce dalla sorgente fredda è maggiore del calore |QBF| che vi entra. Quindi la macchina
composta CA+CB preleva la quantità di calore |QAF| - |QBF| dalla sorgente a TF.
Con la sorgente calda scambia invece la quantità di calore:
|QAC| - |QBC|
e come si è visto è positiva anch’essa, ed è uguale a quella che esce dalla sorgente fredda.
Complessivamente allora la macchina CA+CB sposta la quantità di calore |QAF| - |QBF| = |QAC| |QBC| dalla sorgente fredda alla sorgente calda senza ricevere lavoro dall’esterno.
CA+CB sarebbe pertanto una macchina frigorifera ideale, in contraddizione con il secondo principio
nella formulazione di Clausius.
Se ne conclude che non può essere vera l’ipotesi che B   A . Deve allora valere per forza la
relazione ad essa complementare, e cioè che: B   A .
A questo punto la seconda parte del teorema è dimostrata perché potremmo ripetere l’intero
ragionamento scambiando i ruoli di CA e di CB: partendo dall’ipotesi  A  B e facendo adesso
funzionare a rovescio CB si ottiene che non può essere nemmeno vero che  A  B e che quindi
varrà la sua complementare, cioè  A  B . Dovendo essere vero sia che B   A sia che
 A  B l’unico modo in cui ciò può avvenire è che  A  B : tutti i cicli di Carnot hanno lo stesso
rendimento.
Se poi la macchina B non è una macchina di Carnot, ma una qualunque macchina irreversibile a
due sorgenti allora varrà solo la prima metà della dimostrazione, non potendosi invertire il
funzionamento di una macchina irreversibile in modo che tutte le quantità cambino semplicemente
di segno.
Pertanto risulta dimostrato che per una macchina qualunque, che scambia calore con due sole
sorgenti, il rendimento è   Carnot ed il segno di uguale vale se la macchina è anch’essa di Carnot.
Per quanto riguarda la prima parte del teorema bisogna considerare che per qualunque ciclo
reversibile con più di due sorgenti è possibile una scomposizione del ciclo stesso in tanti tratti di
isoterma ed adiabatica, e quindi una approssimazione con tanti cicli di Carnot. Consideriamo ad
esempio il ciclo in figura 4.3: ad esso è stato sovrapposto un insieme di cicli di Carnot a
temperature di poco differenti fra di loro. Come
si intuisce, l’approssimazione può essere resa
p
tanto migliore quanto più fitta è la suddivisione.
Vediamo adesso che la proprietà di un ciclo di
Carnot :
| QF |
T
 1 F
QC
TC
comporta l’uguaglianza:
  1
| QF | TF

QC
TC
e cioè, eliminando i moduli ed inglobando il
segno nei calori:
QC QF

0
TC TF
V
Figura 4.3: Approssimazione di un ciclo reversibile
qualunque con cicli di Carnot
Si trova subito che una proprietà analoga vale anche un qualsiasi ciclo reversibile con piu di due
sorgenti costituito esclusivamente da isoterme e adiabatiche, come quello che si è usato nella
figura 4.3 per approssimare il ciclo reversibile generico:
IN
UN CICLO REVERSIBILE LA SOMMA, PRESA ALGEBRICAMENTE, DEI RAPPORTI TRA I CALORI
SCAMBIATI E LE RELATIVE TEMPERATURE KELVIN DI SCAMBIO È SEMPRE ZERO:
Qi
T
0
i
Consideriamo ad esempio il ciclo reversibile rappresentato in fig. 4.4, nel quale il calore Q'E
entra alla temperatura T 'E e il calore Q"E alla temperatura T "E , mentre il calore Q'U esce alla
temperatura T 'U e il calore Q"U alla temperatura T "U . Dobbiamo dimostrare che risulta
| Q' E | | Q"E | | Q' U | | Q"U |



 0.
T 'E
T "E
T 'U
T "U
Come si vede in fig. 4.5 prolungando opportunamente l’adiabatica BC e l’adiabatica FG il ciclo
p
p
A
A
Q 'E (T 'E)
Q1
Q3
1
B
H
G
C
Q"E (T "E)
G
D
Q"U (T "u)
B
H
Q2
F
E
Q 'U (T 'U)
Q5
D
3
F
V
Figura 4.4
2
C
Q4
E
Q6
Figura 4.5
V
di partenza può essere scomposto in tre cicli di Carnot.
Nel primo, entra il calore Q 1 alla temperatura T 'E ed esce il calore Q 2 alla temperatura T "U . Nel
secondo, entra il calore Q 3 alla temperatura T 'E ed esce il calore Q 4 alla temperatura T 'U . Nel terzo,
entra il calore Q5 alla temperatura T "E ed esce il calore Q6 alla temperatura T 'U . Per il ciclo 1 risulta
| Q3 | | Q4 |
| Q5 | | Q6 |
| Q1 | | Q2 |

 0 , per il ciclo 2 risulta
 '  0 , per il ciclo 3 risulta

 0.
'
T 'E
T "U
TE
TU
T "E
T 'U
Sommando membro a membro le tre relazioni scritte otteniamo
| Q1 |  | Q3 | | Q5 | | Q4 |  | Q6 | | Q2 |
= 0.



T 'E
T "E
T 'U
T "U
Se a questo punto teniamo conto che è |Q1| + |Q3| = |Q'E | , |Q5|= |Q"E | , |Q4| + |Q6| = |Q 'U| , |Q2| =
|Q"U | , la relazione è dimostrata. È ovvio che la validità potrebbe essere analogamente verificata per
qualsiasi altro ciclo di sole adiabatiche ed isoterme. Quindi per i cicli reversibili con un numero
qualunque di sorgenti si ha:
Qi
T
0
i
Separando ora il calore QE scambiato in entrata dal calore QU scambiato in uscita, la relazione
precedente diventa
|Q |
|Q |
 TE   TU  0 .
E
U
Se ora alle varie temperature di entrata sostituiamo la più
p
grande di esse (Tmax) il valore della prima delle due
sommatorie risulta certamente diminuito. Analogamente,
se nella seconda sommatoria sostituiamo alle temperature
di uscita la più piccola (Tmin), il valore della sommatoria
risulta certamente maggiorato. Per qualsiasi ciclo che non
Tmax
sia un ciclo di Carnot (fig.4.6) risulta dunque

che significa
Tmin
|Q |
| QE |
 U <0
Tmax
Tmin
| Q
| Q
U
|
E
|
>
V
Figura 4.6. La figura considera tre
cicli reversibili di un gas perfetto: per tali
cicli il rendimento è sicuramente inferiore
a quello di un ciclo di Carnot.
Tmin
Tmax
e quindi
 = 1
| Q
| Q
U
|
E
|
< 1
Tmin
= Carnot
Tmax
Quest’ultima relazione mostra ciò che cercavamo e cioè che il rendimento di un ciclo qualunque,
reversibile, è minore di quello di un ciclo di Carnot che scambia calore solo con sorgenti alle
temperature massima e minima fra le quali il ciclo è racchiuso. Per i cicli reversibili il risultato
vale a maggior ragione, dato che come si è visto già per i cicli irreversibili a due sole sorgenti si ha:
  Carnot .