Macchine termiche: ciclo di Carnot
Una macchina termica (o motore termico) è un dispositivo che scambia calore con
l’ambiente (attraverso un fluido motore) producendo lavoro in modo continuo, tramite
un ciclo di trasformazioni. Esempi famosi di macchine termiche sono:
la macchina a vapore (fluido = acqua allo stato liquido e di vapore);
il motore a scoppio (fluido = miscela di aria e benzina);
il motore Diesel (fluido = miscela di aria e gasolio).
Benché non esistano gas veramente ideali né trasformazioni esattamente reversibili,
tali modelli ideali sono molto utili nello studio e progettazione delle macchine termiche.
Studiamo quindi motori ideali basati su cicli di trasformazioni reversibili lungo le quali
non c’è dispersione di energia (ad esempio per attriti e/o turbolenze).
Il motore ideale più famoso è basato sul ciclo di Carnot.
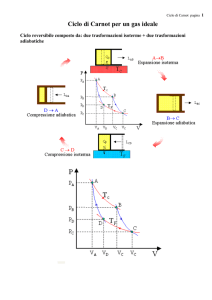
Esso fa uso di un gas ideale e considera un ciclo costituito da
4 trasformazioni reversibili: due isoterme e due adiabatiche
(vedi figura a sinistra). La macchina termica lavora tra
due temperature T1 e T2 (quelle delle due isoterme), e
gli scambi di calore (Q1 e Q2) avvengono solo lungo tali
trasformazioni. La macchina produce un lavoro L pari
all’area del ciclo.
Ciclo di Carnot, calore e lavoro
Una macchina che realizza il ciclo di Carnot può essere
realizzata con un gas ideale confinato in un cilindro :
ab) il gas è in contatto con una sorgente ad alta temperatura
(T1) ed espandendosi isotermicamente assorbe il calore Q1;
bc) la sorgente viene sostituita con una parete isolante e il gas
si espande adiabaticamente;
cd) la parete isolante viene sostituita con una sorgente a bassa
temperatura (T2) alla quale, nella compressione isoterma, il gas
cede il calore Q2;
da) la sorgente viene di nuovo rimpiazzata da una parete
isolante e il gas è compresso adiabaticamente.
In un ciclo la variazione di energia interna è nulla. Quindi, per
la prima legge della termodinamica è L = Q. Nel caso presente
il lavoro prodotto in un ciclo è pari a L = |Q1| − |Q2|
Anche la variazione di entropia nel ciclo deve essere nulla, dato che S è una funzione
di stato. Inoltre, essendo tutte le trasformazioni reversibili e ∆S = 0 nelle adiabatiche:
|Q1| |Q2|
∆S =
−
=0
T1
T2
⇒
|Q1| |Q2|
=
T1
T2
Ciclo di Carnot, entropia
|Q2 |
1|
La relazione precedente: |Q
=
T1
T2 è basata sull’ipotesi che l’entropia sia una funzione
di stato, ma è possibile dimostrarla direttamente. Infatti, per le due isoterme, vale:
Q1 = nRT1 log
Vb
,
Va
Q2 = nRT2 log
Vd
,
Vc
∆S =
Q1 Q2
Vb
Vd
+
= nR log
+ log
.
T1 T2
Va
Vc
D’altra parte, per le due adiabatiche vale T1Vbγ−1 = T2Vcγ=1 e T2Vdγ−1 = T1Vaγ−1.
Vc
Vb
= , da cui ∆S = 0.
Dividendo membro a membro si ottiene
Va Vd
E’ possibile usare tale proprietà del ciclo di Carnot per dimostrare che in un ciclo in
cui N sorgenti a temperatura Ti scambiano calore Qi con il sistema, vale:
N
X
Qi
i=1
Ti
=0
se tutte le trasformazioni sono reversibli.
(da qui si dimostra che l’entropia come l’abbiamo definita è una funzione di stato)
Rendimento di macchine termiche ideali: macchina di Carnot
In una macchina termica viene fornito del calore Qa e
prodotta energia meccanica come lavoro L. La qualità di
tale trasformazione è misurata dal rendimento η definito
come
energia ottenuta
L
η=
=
energia assorbita |Qa|
Il rendimento di una macchina che realizza il ciclo di Carnot
è pari a
|Q2|
|Q1| − |Q2|
=1−
ηC =
|Q1|
|Q1|
→
T2
ηC = 1 −
T1
dove le temperature sono espresse in kelvin.
Notare: η > 1 sempre, anche per macchine ideali. Nello schema sopra riportato,
notare come parte del calore fornito alla macchina (Q1) sia sempre ceduto alla sorgente
a temperatura più bassa (Q2); di conseguenza il lavoro prodotto L potrà al più essere
pari alla differenza tra i due.
Enunciato di Kelvin
Si arriva quindi alla conclusione che non potrà mai essere
realizzato il motore perfetto (vedi schema qui accanto), in
cui il calore prelevato da un’unica sorgente è completamente
trasformato in lavoro.
Tale conclusione porta in modo naturale al seguente enunciato alternativo della
seconda legge della termodinamica (enunciato di Kelvin):
Non esiste un ciclo termodinamico avente come unico risultato l’acquisizione di calore
da un’unica sorgente termica e la sua totale trasformazione in lavoro
Rendimento di altre macchine termiche
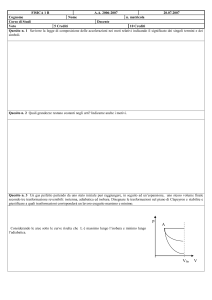
Ciclo di Stirling - costituito da due isoterme e due isocore.
Il rendimento ηs di tale ciclo è inferiore a quello del ciclo di
Carnot ηc:
ηC
|Q1| − |Q2| (|Q1| − |Q2|)/|Q1|
=
=
< ηC
ηS =
|Q1| + |Q|
(|Q1| + |Q|)/|Q1|
1 + |Q|/|Q1|
Ciclo Otto (motore a 4 tempi) – Non è un ciclo che lavora tra
due sole temperature: non ci sono isoterme. Il calore assorbito è
quello scambiato nella trasformazione 1 → 2. Per un gas ideale:
Q1,2 = ∆Eint = ncV (T2 − T1),
L = −(∆Eint,23 + ∆Eint,41) = −ncV (T3 − T2) − ncV (T1 − T4)
Ricordando che per una trasformazione adiabatica T V γ−1=cost., otteniamo
η4−tempi
γ−1
ccp −1
γ−1
ncV 1 − (V2/V3)
(T2 − T1)
L
V2
V2 V
=
=
= 1−
= 1−
|Q1,2|
ncV (T2 − T1)
V3
V3
Il rapporto V2/V3 è detto rapporto di compressione.
Macchine frigorifere
Una macchina termica che trasferisce calore da una sorgente
fredda ad una sorgente calda costituisce una macchina frigorifera
(o frigorigena). Una macchina di Carnot che funziona “al
contrario” è una macchina frigorifera.
Lo schema qui a
lato precisa le relazioni tra il lavoro che si deve fornire
alla macchina frigorifera e i calori scambiati con le sorgenti
termiche. L’efficienza di una macchina frigorifera è misurata con
il parametro
energia utile
|Qu|
ε=
=
energia assorbita
L
Per il frigorifero di Carnot abbiamo
|Q2|
T2
T2/T1
1 − ηC
1
=
=
=
=
−1
εC =
|Q1| − |Q2| T1 − T2 1 − (T2/T1)
ηC
ηC
dove ηC è il rendimento della macchina di Carnot quando funziona nel verso usuale.
Secondo principio, enunciato di Clausius
Cosı̀ come il motore perfetto, anche il frigorifero perfetto
(schematizzato qui a fianco) non esiste! Infatti, in tal caso la
variazione di entropia complessiva del sistema (sorgenti termiche
+ gas) sarebbe pari a
∆S = −
|Q| |Q|
+
<0
T2
T1
in contrasto con la seconda legge della termodinamica (dato che
il sistema è chiuso).
Questo porta al seguente enunciato alternativo (di Clausius) della seconda legge:
Non esiste una trasformazione il cui unico risultato è il trasferimento di calore da una
sorgente a temperatura più bassa ad una a temperatura più alta
Rendimento delle macchine reali
Tra tutte le macchine termiche che operano tra due sole temperature T1 e T2 (con
T1 > T2), la macchina di Carnot è quella con il rendimento più elevato.
Supponiamo di avere una macchina di rendimento ηx > ηC .
Accoppiamola a un frigorifero di Carnot operante tra le stesse
temperature e che utilizza tutto il lavoro prodotto dalla nostra
macchina. Otteniamo una macchina che: (1) non utilizza lavoro
esterno e che, (2) scambia le quantità di calore |Q1| − |Q01| e
|Q02| − |Q2| con le sorgenti alle temperature T1 e T2
Dato che il lavoro prodotto dalla macchina termica è pari a quello utilizzato dal
frigorifero di Carnot, |Q1| − |Q2| = |Q01| − |Q02|, da cui |Q1| − |Q01| = |Q2| − |Q02| = Q.
Se ηx > ηC abbiamo
ηx > ηC
⇒
|L|
|L|
>
|Q01| |Q1|
→
Q = |Q1| − |Q01| > 0
Ma in questo modo, avremmo costruito un frigorifero perfetto!
Nessuna macchina termica reale che lavora fra due temperature
può avere un rendimento superiore a quella di Carnot.