Ciclo di Carnot

Ciclo di Carnot
CICLO DI CARNOT
Una macchina termica è un sistema che, operando ciclicamente, produce lavoro assorbendo calore da
un termostato.
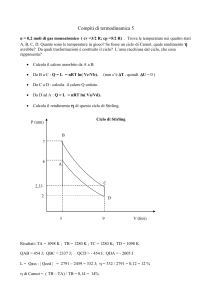
Il ciclo termico di Carnot è composto da quattro trasformazioni termodinamiche: due isoterme e due
adiabatiche. Nel caso di un ciclo ideale, le trasformazioni sono considerate reversibili.
Si prende in considerazione un cilindro contenete un gas perfetto, però in senso generale si potrebbe
usare un qualsiasi fluido.
h2
h3
3
h1
h4
2
4
1
1
S1
S2
S1
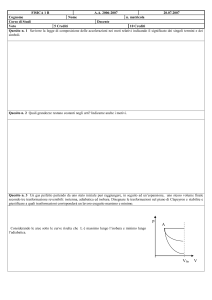
Nel piano di Clapeyron il ciclo assume la seguente forma:
P
P1
TA
1
P2
4
2
P4
TB
2
P3
V1
V4
V2
V3
V
Analisi del ciclo
Condizioni iniziali
All’inizio del ciclo il gas si trova nello stato 1 nelle seguenti condizioni:
P1, V1, T1 = TA
Prima trasformazione - espansione isoterma
La prima trasformazione termodinamica che subisce il gas è una isoterma, cioè la temperatura del gas
si mantiene costante. Per eseguire tale trasformazione si pone a contatto con una sorgente di calore, S1, il
cilindro contenente il gas. Il gas subisce una espansione isoterma raggiungendo lo stato 2. Al termine
della trasformazione le condizioni del gas sono:
P2,
V2,
T2 = T1 = TA
1
Ciclo di Carnot
In questa trasformazione il gas assorbe una quantità di calore QA = Q12. Poiché la temperatura
si deve mantenere costante, tutta l’energia assorbita viene ceduta all’esterno del sistema sotto
forma di lavoro meccanico, L12. A causa dello stretto collegamento tra energia interna, U, e la
temperatura del gas, T2 = TA, si ha che l’energia interna non varia, pertanto il primo principio
della termodinamica assume la seguente forma:
U12 = Q12 - L12
U12 = 0
QA = Q12 = L12
dove U12 è la variazione di energia interna subita dal gas nella trasformazione isoterma.
Il lavoro compiuto dal gas sull’ambiente circostante è positivo e vale:
V
V
P
Q A = Q12 = L12 = n  R  T2  ln 2 = n  R  T A  ln 2 = n  R  T A  ln 1
V1
V1
P2
Seconda trasformazione - espansione adiabatica
La seconda trasformazione subita dal gas è una adiabatica, cioè il gas non scambia calore con
l’ambiente circostante. Per fare questo si isola il cilindro allontanandolo da qualsiasi sorgente di
calore. Il calore scambiato, Q23, è nullo. Nella trasformazione il gas si espande, il lavoro viene
fatto dal sistema sull’ambiente circostante ed il suo valore è positivo. Tale lavoro viene fatto a
scapito dell’energia interna del gas, che diminuisce. Come conseguenza si ha che la temperatura
del gas subisce una diminuzione, portandosi al valore di T3 = TB. Il gas si porta nello stato 3
assumendo i seguenti valori, per quanto riguarda le variabili termodinamiche:
P3, V3, T3 = TB,
Applicando il primo principio della termodinamica alla trasformazione adiabatica si ha:
U23 = Q23 - L23
poiché
Q23 = 0
allora
U23 = - L23
Il lavoro fatto dal gas sull’ambiente circostante è:
R
L 23 = n  c V  T2 - T3 = n  c V  T A  T B  = -n  c V  T3 - T2 = n 
 T2 - T3 
 -1
La variazione di energia interna subita dal gas è:
U23 = ncV(T3 - T2) = ncV(TB - TA) < 0
Terza trasformazione - compressione isoterma
La terza trasformazione è una isoterma. Il cilindro, contenente il gas, viene posto a contatto
con una sorgente di calore, S2, che si trova ad una temperatura più bassa della sorgente
precedente. Il pistone viene abbassato, la trasformazione è, pertanto, una compressione isoterma.
L’ambiente circostante fa un lavoro sul sistema, l’energia interna non cambia ed il gas cede
calore, QB, alla sorgente S2. Infatti il gas riceve dall’esterno dell’energia mediante il lavoro
meccanico e tende ad aumentare la sua energia interna; poiché l’energia interna non deve variare
(trasformazione isoterma), allora il gas cede all’esterno l’energia ricevuta sotto forma di calore.
Nella trasformazione il gas passa dallo stato 3 allo stato 4. I parametri, che descrivono lo stato
termodinamico del gas, sono i seguenti:
P4, V4, T4 = T3 = TB
Per il primo principio della termodinamica si hanno le seguenti situazioni:
U34 = Q34 - L34 = QB - L34
U34 = 0
QB = Q34 = L34
2
Ciclo di Carnot
Il lavoro compiuto dall’ambiente circostante sul sistema è negativo e vale:
V
V
P
Q B = Q34 = L34 = n  R  T3  ln 4 = n  R  TB  ln 4 = n  R  TB  ln 3
V3
V3
P4
Quarta trasformazione - compressione adiabatica
Il cilindro, contenente il gas, viene isolato dall’ambiente circostante e si comprime il pistone.
La trasformazione eseguita è una compressione adiabatica. Il calore, Q41, scambiato è nullo, il
lavoro, L41, fatto dall’ambiente circostante sul sistema va ad aumentare l’energia interna del gas.
Il gas passa dallo stato 4 allo stato 1. I parametri del sistema sono i seguenti:
P1, V1,
T1 = TA
Applicando il primo principio della termodinamica alla trasformazione adiabatica si ha:
U41 = Q41 - L41
Q41 = 0
U41 = - L41
R
L 41 = n  c V  T4 - T1 = - n  c V  T1  T 4  = n 
 T4 - T1 
 -1
L 41 = n  c V  TB - T A = - n  c V  TA  TB 
quindi
U 41 = - L 41 = n  c V  TA  TB   0
Analisi dei dati
Il sistema parte dallo stato 1 e ritorna allo stato 1, pertanto la sua energia interna, alla fine del
ciclo, non varia. Infatti si ha:
U = U11 = 0
U11 = U12 + U23 + U34 + U41
U11 = 0 + ncV(TB - TA) + 0 + ncV(TA - TB) = 0
U = U11 = 0
Si tenga presente che l’energia interna è una funzione di stato, la sua variazione dipende solo
dai valori iniziale e finale. Se questi ultimi coincidono allora la variazione è zero.
Il verso di esecuzione del ciclo termico è orario, pertanto il lavoro totale che il sistema fa
sull’ambiente circostante è positivo. Il lavoro totale che viene compiuto nel ciclo è:
LTot = L12 + L23 + L34 + L41
V2
V
LTot = n  R  T A  ln
+ n  c V  T A  TB  + n  R  T B  ln 4 + n  c V  TB - T A 
V3
V1
Al secondo membro della uguaglianza, il secondo ed il quarto termine sono uguali e opposti,
pertanto la loro somma è nulla. Quindi il lavoro totale è:
V
V
LTot = n  R  T A  ln 2 + n  R  T B  ln 4 = QA + QB
V3
V1
QA è una quantità positiva. QB è una quantità negativa. Se si prendono i valori assoluti delle
quantità di calore scambiate, il lavoro totale che il sistema compie sull’ambiente circostante è:
V
V
LTot = n  R  T A  ln 2 - n  R  T B  ln 3 = QA - QB
V4
V1
Tenendo conto che in una trasformazione adiabatica si ha:
T A  V2 - 1 = TB  V3 - 1
si verifica che
V2 V3
=
V1 V4
3
Ciclo di Carnot
allora il lavoro è:
LTot = n  R  T A  ln
V2
V
V
- n  R  TB  ln 2 = n  R  ln 2  T A - T B 
V1
V1
V1
Poiché
Q A = n  R  T A  ln
si ha
LTot = n  R  T A  ln
V2
V1
V2 T A - T B 
T - T B 
= QA A

TA
V1
TA
Si definisce rendimento di una macchina termica (la definizione è di validità generale) il
rapporto fra il lavoro, LTot, che un sistema fa sull’ambiente circostante ed il calore totale
assorbito, QA, da sistema:
Q
Q  QB Q A - QB
T - TB
T
= A

= 1- B = A
= 1- B < 1
QA
QA
QA
TA
TA
Il rendimento è sempre minore di uno. Il rendimento del ciclo di Carnot aumenta
all’aumentare della differenza fra le temperature TA e TB.
Dagli scritti di Sadi Carnot (S.Carnot: La potenza motrice del fuoco), E. Clapeyron ha
dimostrato che il rendimento, , del ciclo di Carnot era il massimo ottenibile da una
macchina termica (teorema di Carnot). Cioè, il rendimento termico di un arbitrario ciclo
reversibile, funzionante con i medesimi termostati (i due termostati sono la sorgente a
temperatura più alta, TA, e la sorgente a temperatura più bassa, TB), non può essere superiore al
rendimento del ciclo di Carnot reversibile. Un’importante conseguenza del teorema di Carnot
è che tutte le macchine di Carnot che lavorano fra gli stessi due termostati hanno lo stesso
rendimento. Questo risultato indica che il rendimento della macchina di Carnot è un
parametro universale, indipendente cioè dalla natura specifica del sistema che costituisce la
macchina (cioè è indipendente dalla natura del fluido di lavoro). Il rendimento dipende,
cioè, solo dalle temperature dei due termostati.
Indicando con R il rendimento di una macchina di Carnot che funzioni mediante
trasformazioni reversibili e I il rendimento della stessa macchina che funzioni mediante
trasformazioni irreversibili e con gli stessi termostati, si verifica sempre che il rendimento
della macchina con trasformazioni irreversibili è sempre più piccolo di quello della
macchina con trasformazioni reversibili.
I < R
Dal libro di Sadi Carnot (La potenza motrice del fuoco), E. Clapeyron ha mostrato che per il
ciclo termico di Carnot vale il seguente importante teorema: Tra tutte le macchine termiche operanti tra
le stesse temperature estreme (TA e TB), la macchina di Carnot è quella dotata del massimo rendimento.
Inoltre il rendimento del ciclo di Carnot non dipende dalla natura dell’agente termico presente nella
macchina, ma è unicamente funzione dei due valori della temperatura. Quindi il rendimento del ciclo di
Carnot è il massimo che si può ottenere da una macchina termica. Inoltre tutte le macchine di Carnot che
lavorano fra gli stessi due termostati hanno lo stesso rendimento. In sintesi, se il rendimento di una
qualsiasi macchina termica reversibile è Rev, questo valore non può mai essere superiore al rendimento,
Rev(Carnot), di un ciclo reversibile di Carnot realizzato fra le stesse temperature TA e TB
[RevRev(Carnot)]. Pertanto si ha:
Re v  Re v Carnot   1 
4
TB
TA
Ciclo di Carnot
Il rendimento, Irrev(Carnot), di un ciclo irreversibile di Carnot è sempre più piccolo di quello,
Rev(Carnot), di un ciclo di reversibile di Carnot realizzati fra le stesse temperature estreme TA e TB
[Irrev(Carnot) < Rev(Carnot)]. Il rendimento di un ciclo irreversibile di Carnot:
Irre v  1 
QB
T
 Re v  1  B
QA
TA
Per un generico ciclo termodinamico vale una importante disuguaglianza di Clausius. Tenendo
presente il rendimento sia del ciclo reversibile che del ciclo irreversibile di Carnot si ricava:

QB
Q
Q
Q
Q
T
  B   B   A  A  B 0
QA
TA
TB
TA
TA
TB
Il segno di uguale (=) vale per il ciclo reversibile di Carnot; il segno di disuguaglianza (<) vale per
il ciclo irreversibile di Carnot.
Prendendo i valori algebrici e non quelli assoluti, si ha:
QA
Q
 B 0
TA
TB
Questa relazione la si può generalizzare al caso in cui si una un ciclo termico che utilizza diverse sorgenti
di calore (Q1, Q2, Q3, Q4,..... Qn) che si trovano a diverse temperature (T1, T2, T3, T4, .......Tn,). La
relazione in forma sintetica si scrive:
Q1 Q 2 Q 3 Q 4
Q
  
.........  n  0 
T1 T 2 T 3 T 4
Tn
n
i

Ti
i 1
Q
0
Questa importante relazione è detta disuguaglianza di Clausius e serve per giudicare la fattibilità
di un ciclo termico che viene proposto. Nelle più generali trasformazioni termodinamiche, la temperatura
cambia con continuità ed il sistema scambia quantità elementari di calore, Q, con l’ambiente circostante.
Pertanto in un ciclo termico qualsiasi la relazione di Clausius diventa:
n

i 1
Q i
0
Ti
 Il segno di uguaglianza (=) vale per un ciclo reversibile


Il
segno
di
disuguaglianza
(<)
vale
per
un
ciclo
irreversibile


 
Le quantità Qi ovvero Qi sono positive se il calore è assorbito dal sistema, mentre sono negative
se vengono cedute dal sistema all’ambiente circostante.
Quando si progetta un ciclo termico è necessario che contemporaneamente soddisfi alle due
seguenti condizioni: 1) il rendimento non deve essere superiore al ciclo di Carnot, che ha due sorgenti di
calore le cui temperature siano la massima e la minima del ciclo che si sta progettando; 2) deve essere
soddisfatta la relazione di Clausius.
5