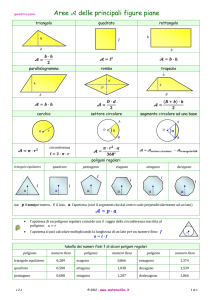
Definizione: si dice regolare un poligono equilatero
ed equiangolo.
Proprietà: ogni poligono regolare è inscrittibile e
circoscrittibile , e le due circonferenze hanno lo stesso centro.
Definizione: si dice apotema di un poligono
regolare il raggio del cerchio inscritto nel
poligono.
Se è noto il raggio R del cerchio circoscritto e il lato del
poligono regolare, l’apotema si trova applicando il teorema di
Pitagora.
Tabella dei numeri fissi per
calcolare l’apotema
Poligono regolare
f
Triangolo equilatero 0,289
Quadrato
0,5
Pentagono
0,688
Esagono
0,866
Ettagono
1,038
Ottagono
1,207
Ennagono
1,374
Decagono
1,539
Proprietà: in ogni poligono regolare il rapporto tra
l'apotema e il lato è costante, dipende solo dal numero dei lati
del poligono. A tale costante del poligono si dà il nome di
numero fisso:
Per trovare l'apotema, noto solo il lato del poligono regolare,
si usa fornire nella geometria studiata nelle medie inferiori una
tabella di numeri fissi.
L'apotema si trova moltiplicando il lato per la
costante del poligono:
L'apotema si può calcolare con l'aiuto della trigonometria,
nota l'ampiezza a dell’angolo del poligono:
.
Poiché in ogni poligono regolare il rapporto tra l'area e il
quadrato del suo lato è costante, dipende solo dal numero dei
lati del poligono, indichiamo tale costante con
.
APOTEMA = AL
RAGGIO
Tabella dei numeri fissi per
calcolare l’area di un poligono
regolare
Poligono regolare
Triangolo equilatero 0,433
Quadrato
1
Pentagono
1,720
Esagono
2,598
Ettagono
3,634
Ottagono
4,828
L'area del poligono regolare si calcola :
Ennagono
6,182
Nella geometria studiata nelle medie inferiori si usa fornire
una tabella di costanti.
Decagono
7,694
QUINDI L’AREA DI UN POLIGONO REGOLARE LA POSSIAMO CALCOLARE IN 2 MODI
1) PERIMETRO* APOTEMA /2 (che gia’ conosciamo)
2)
SERVENDOCI DELLATEABELLA DEI NUMERI FISSI