PROGRAMMA DI MATEMATICA
Anno scolastico 1998-999
classe V B geom.
INS. SALARIS GIANFRANCO
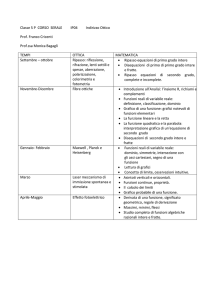
ALGEBRA
Disequazioni di primo e secondo grado, fratte. Equazioni algebriche
ANALISI NUMERICA
Funzioni e grafici
Funzioni e campo di esistenza di una funzione: ricerca del campo di esistenza
di semplici funzioni razionali intere, fratte e irrazionali.
Limiti di funzioni reali
Definizioni fondamentali, verifica e calcolo di semplici limiti di una funzione.
Funzioni derivate e primitive
Derivata di una funzione: definizione, calcolo e significato geometrico; applicazioni
per la determinazione dell'equazione della retta tangente ad una curva e per la ricerca
dei massimi
e minimi di una funzione.
Asintoti: definizione e loro ricerca.
STUDIO di semplici funzioni intere, fratte e trascendenti.
Problemi di massimo in diversi ambiti disciplinari: costruzioni contabilità
impianti.
Il calcolo integrale
Integrali indefiniti e definiti: applicazioni per il calcolo di aree e di volumi
di solidi di rotazione.
Risoluzione di problemi tecnici in cui si fa uso del calcolo integrale.
Equazioni differenziali: cenni e risoluzioni si semplici equazioni del primo
ordine e lineari : applicazione alla risoluzione di alcuni problemi tecnici
(anche mediante l'uso dell'elaboratore).
Matrici : calcolo matriciale e risoluzione di sistemi lineari di n equazioni ad n
incognite (anche con l'uso dell'elaboratore).
Le teorie formali
L'assetto formale di una teoria matematica: L'antinomia di Russel. Il teorema di Godel
Il sistema assiomatico di Euclide La nascita delle geometrie non euclidee.
Modelli di geometrie non euclidee.
1
L'insegnante
[email protected]
2