compitino-10-6

CORSO DI LAUREA IN SCIENZE BIOLOGICHE
II prova parziale di FISICA, 10 Giugno 2005
1) Un cubo di lato L = 20 cm viene immerso in acqua. Il cubo galleggia con i 2/3 del suo volume immerso.
Si determinino:
a) la densità C del materiale di cui è costituito il corpo;
b) l’intensità Fapp della forza che deve essere applicata dall’esterno per mantenere il corpo completamente
immerso in acqua.
2) Un gas perfetto monoatomico costituito da n=2 moli compie la seguente trasformazione ciclica:
A B: espansione isobara a pressione pA= 3 atm da VA= 1 litro a VB=2 litri;
B C: trasformazione isocora da pB a pC= 1 atm;
C D: compressione isoterma da VC a VD = 1 litro;
D A: trasformazione isocora da pD a pA = 3 atm.
Si svolgano i seguenti punti:
a) si disegni nel piano pV la trasformazione ciclica, si determinino per gli stati A, B, C e D le variabili
termodinamiche (P,V,T) e si calcoli il lavoro W svolto dal gas;
b) si determino per i quattro rami della trasformazione e per l’intero ciclo la variazione Eint di energia
interna ed il calore Q scambiato.
[Nota: R= 8.31 J/Kmole =0.082 l atmo /Kmole]
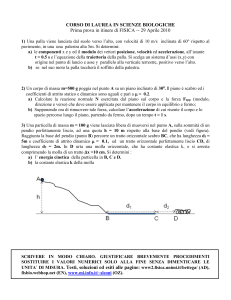
3) Due piani infinitamente estesi sono posti a distanza d = 20 cm. I piani sono elettricamente carichi con carica
opposta e densità di carica superficiale uniforme, pari, in valore assoluto, a  = 20 nC/m2. Una pallina di
massa trascurabile e carica positiva q = +1 nC è mantenuta in equilibrio tra i due piani mediante un filo
isolante di lunghezza L = 10cm, vincolato al piano carico positivamente, come mostrato in figura.
Si svolgano i seguenti punti (trascurando gli effetti della forza gravitazionale):
a) si determinino il campo elettrico E fra i due piani e la tensione T del filo,
specificando per entrambi il modulo, la direzione ed il verso;
b) Si supponga di tagliare il filo: calcolare il lavoro fatto dalla forza elettrostatica
per portare la pallina dal punto di equilibrio precedente sino alla lamina di carica
negativa.
[Nota: 0 = 8.85 10-12 C2/Nm2]
SCRIVERE IN MODO CHIARO
GIUSTIFICARE BREVEMENTE I PROCEDIMENTI
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE
RIPORTARE SEMPRE LE UNITA` DI MISURA
SOLUZIONE ESERCIZIO 1
a) Perché il corpo galleggi sull’acqua si deve avere equilibrio fra la forza peso Fg e la spinta di
Archimede FA


Fg  FA  0
Proiettando l’equazione vettoriale precedente su un asse y di riferimento, verticale ed orientato dal
basso verso l’alto, si ottiene
 Fg  FA  0
Mentre la forza peso agisce su tutta la massa m del corpo, la spinta di Archimede agisce solo sulla
massa mf di fluido spostato
mg  m f g
 CV g   H O V f g   H O
2
2
2
V g
3
da cui si ricava
C 
2
2
kg
kg
 H 2O  10 3 3  667 3
3
3
m
m
b) Perché il corpo rimanga sommerso completamente in acqua è necessario applicare una forza Fapp
diretta verticalmente verso il basso tale che



Fapp  Fg  FA  0
 Fapp  Fg  FA  0
da cui si ricava
Fapp  FA  Fg  m f g  mg  (m f  m) g
In questo caso la massa di fluido spostato corrisponde al volume occupato dall’intero corpo, ora
completamente immerso:
Fapp  (m f  m) g  (  H 2OV   CV ) g  (  H 2O   C )Vg
2
1
 H 2O ) L3 g   H 2O L3 g
3
3
1
kg
m
  10 3 3  (0.2m) 3  9.8 2  26 N
3
m
s
 (  H 2O 
SOLUZIONE ESERCIZIO 2
a) La trasformazione compiuta dal gas è il ciclo rappresentato
in figura.
Per ogni stato le variabili termodinamiche (p,V,T) si
possono determinare utilizzando l’equazione di stato dei
gas perfetti:
stato A:
p AV A 3  10 5 N / m 2  10 3 m 3
p A  3 atm, V A  1 litro  10 m , TA 

 18 K
nR
2  8.31 J / Kmole
stato B:
p V
3  10 5 N / m 2  2  10 3 m 3
p B  p A  3 atm, VB  2 litri  2  10 3 m 3 , TB  B B 
 36 K
nR
2  8.31 J / Kmole
stato C:
pCVC 1  10 5 N / m 2  2  10 3 m 3
3
3
pC  1 atm, VC  VB  2 litri  2  10 m , TC 

 12 K
nR
2  8.31 J / Kmole
stato D:
nRT D 2  8.31 J / Kmole  12 K
TD  TC  12 K , VD  V A  1 litro  10 3 m 3 , p D 

 2  10 5 N / m 2  2 atm
3
3
VD
10 m
3
3
Il lavoro svolto dal gas durante l’intero ciclo è pari all’area racchiusa dalla curva nel piano pV:
C
C
V
nRT D
dV  p A  (VB  V A )  nRT D ln C
V
VD
D
WTOT  p A  (VB  V A )   pdV  p A  (VB  V A )  
D
 3  10 N / m  10 3 m 3  2  8.31 J / Kmole  12 K ln2  3  10 2 J  138 J  162 J
5
2
Il lavoro è positivo, infatti il ciclo è percorso in senso orario.
b) Le quantità Eint, Q e W relative a ciascun ramo del ciclo si possono calcolare applicando il primo
principio della termodinamica:
Eint  Q  W
, e ricordandosi che
cV 
3
R
2
e
cp 
5
R
2
Trasformazione AB (isobara):
5
Q AB  nc p (TB  T A )  2( 8.31J / Kmole)  18K  747.9 J
2
W AB  p A (V B  V A )  3  10 5 N / m 2  10 3 m 3  300 J
E AB  Q AB  W AB  448 J
Trasformazione BC (isocora):
il gas non compie lavoro, dato che il volume rimane costante
3
QBC  ncV (TC  TB )  2( 8.31J / Kmole)  24 K  598.3J
2
WBC  0
E BC  QBC  598J
Trasformazione CD (isoterma):
non ho variazione di energia interna, dato che la temperatura è costante
ECD  QCD  WCD  0
D
nRTC
V
dV  nRTC ln C  nRTC ln 2  2  (8.31J / moleK )  12 K ln 2  138.2 J
V
VD
C
QCD  WCD  
Trasformazione DA (isocora):
il gas non compie lavoro, dato che il volume rimane costante
3
QDA  ncV (T A  TD )  2( 8.31J / Kmole)  6 K  149.6 J
2
WBC  0
E BC  QBC  150 J
Intero Ciclo:
l’energia interna non cambia dato che lo stato finale è uguale allo stato iniziale, quindi il calore totale
scambiato è pari al lavoro svolto dal gas, calcolato al punto a):
ETOT  QTOT  WTOT  0
QTOT  WTOT  162 J
Si noti che:
ETOT  E AB  E BC  E CD  E DA  0
QTOT  Q AB  QBC  QCD  QDA  162 J
WTOT  W AB  WBC  WCD  WDA  162 J
SOLUZIONE ESERCIZIO 3
a) Nella regione interna alle due lamine piane infinite il campo elettrico è diretto perpendicolarmente
alle due lamine piane, con verso uscente dalla lamina positiva,
ed intensità costante, ossia:
  
E
i 
0
20  10 9 C / m 2
 2.26  10 3 N / C
8.85  10 12 C 2 /Nm 2
ove i indica il versore associato all’asse x, come mostrato in
figura.
All’equilibrio la tensione T del file è uguale ed opposta alla
forza elettrostatica


Fe  qE
ossia


 
T  qE  q i  10 9 C 
0

20  10 9 C / m 2 
i  (2.26  10 6 N ) i
12
2
2
8.85  10 C /Nm
b) Il lavoro fatto dalla forza elettrostatica Fe, costante, è dato da:
 

L  Fe  s  q (d  L)  10 9 C 
0
20  10 9 C / m 2
(0.2  0.1)m  2.26  10 7 J
8.85  10 12 C 2 /Nm 2