
EsercizidiFISICA(6)
1. Un pezzo di ghiaccio, di massa mg = 3.0 kg e alla temperatura Tg = 253 K viene
immerso in una massa di acqua pari a ma = 1.0 kg alla temperatura Ta = 373 K. Il
sistema è contenuto in un recipiente a pareti adiabatiche.
Determinare la temperatura finale Tf del sistema.
(λf=3.3•105 J/kg, c(acqua)=4186.8 J/kg K, c(ghiaccio)=2051.5 J/kg K)
2. Un sottile guscio sferico di gomma, un palloncino, di massa M = 50 g, viene riempito di
azoto e immerso in un lago. Trascurando le forze di tensione della gomma, si determini
la massa di azoto (massa molare pari a mN2 =28 g) che deve essere racchiusa nella cavità
affinché il guscio sferico si trovi in equilibrio statico a una profondità h = 100 m, dove la
temperatura dell’acqua è T = 4.0 °C.
3. Un gas perfetto biatomico (cV = 5/2R, cP = 7/2R, γ = 7/5 = 1.4) dallo stato iniziale con pi =
2.0 atm e Vi = 0.5 l, raggiunge lo stato finale in cui Vf = 2.0 l attraverso tre diversi
percorsi reversibili: a) espansione adiabatica; b) espansione isoterma seguita da
un’isocora; c) un’isocora seguita da una espansione isobara. Determinare il lavoro fatto
ed il calore scambiato per ciascun tipo di percorso (anche in segno).
4. Una certa quantità di aria, il cui stato iniziale è caratterizzato dalle coordinate
termodinamiche Vi = 5.0 m3, pi = 4.0 atm e Ti = 60.0 °C, subisce una trasformazione fino
ad uno stato finale caratterizzato da Vf = 3.0Vi e pf = 1.0 atm. La trasformazione seguita
è una trasformazione del tipo pVk = cost con l’esponente k incognito. Nell’ipotesi che
l’aria sia assimilabile ad un gas perfetto biatomico, si determini:
a) l’esponente k della trasformazione;
b) il lavoro L compiuto dall’aria;
c) la variazione di energia interna, ΔEint, dell’aria;
d) la quantità di calore, Q, assorbita dall’aria.
5. Una macchina reversibile utilizza come fluido una quantità di sostanza n = 1.0 mol di un
gas perfetto biatomico che esegue il ciclo costituito dalle seguenti 3 trasformazioni: 1)
dallo stato iniziale (p1 = 5.0 atm e T1 = 20° C) il gas viene fatto espandere lungo
un’isoterma fino ad una pressione p2 = 1.0 atm; 2) a pressione costante, p2, il gas viene
riportato sull’adiabatica passante per lo stato iniziale; 3) seguendo l’adiabatica il gas
viene quindi riportato allo stato iniziale. Si determini:
a) il lavoro L e il calore Q scambiati dal gas in un ciclo;
b) il rendimento del ciclo;
c) la variazione di entropia lungo la trasformazione isobara.
6. Una quantità pari a n = 1.0 mol di un gas perfetto, contenuta in un cilindro dotato di
pistone libero di scorrere senza attrito, subisce in un primo tempo una lenta espansione
senza scambio di calore con l’esterno, fino a raddoppiare il volume iniziale. In seguito, il
gas subisce una lenta compressione a temperatura costante fino a tornare al volume
iniziale. Sapendo che la temperatura iniziale e finale del gas sono T1 = 61°C e
T2 = -20°C, si determinino:
a) il rapporto fra i calori specifici a pressione e volume costante del gas;
b) l’eventuale variazione di entropia del gas.
7. Una macchina termica basata sull’uso di un gas ideale segue un ciclo composto da due
isobare e due adiabatiche (tutte reversibili). La macchina fa uso di n = 5.0 mol di gas e le
due isobare sono alle pressioni pA = 20.0 atm e pB = 10.0 atm, mentre l’espansione
isobara a pressione più elevata si svolge tra i volumi V1 = 5.0 l e V2 = 10.0 l.
Supponendo di poter far lavorare la macchina termica sia con un gas monoatomico che
con uno biatomico, determinare:
a) la quantità di calore assorbito dai gas in un ciclo e per quale dei due è più
elevata;
b) la temperatura minima raggiunta da ogni gas lungo il ciclo;
c) l’espressione del rendimento della macchina specificando per quale gas è più
elevato
8. Un recipiente cilindrico con pareti adiabatiche, di sezione A = 0.3 m2 e lunghezza l = 1.0
m, è suddiviso in due camere uguali per mezzo di un pistone a tenuta (di spessore e
massa trascurabili). Il pistone è adiabatico e può scorrere senza attrito lungo le pareti del
cilindro. In una delle camere viene inserita una molla di costante elastica k = 100 N/cm,
di lunghezza a riposo pari a l/2. L’altra camera viene riempita con n moli di un gas
ideale. Sapendo che all’immissione del gas la molla si accorcia di 15 cm e che per farla
riallungare di 5 cm la temperatura del gas deve essere diminuita di 120 K, determinare:
(a) il numero di moli n di gas ideale immesso
(b) la temperatura T0 iniziale del gas;
(c) la quantità di calore Q persa dal gas durante la diminuzione di temperatura.
9. Una mole di gas monoatomico a pressione pA = 1.0 atm, volume VA = 22.4 l e
temperatura TA = 273 K compie le seguenti trasformazioni reversibili: A → B isobara
con VB = 1.2VA; B → C isocora con pC = 1.2pA; C → D isobara con VD = VA; D → A
isocora per chiudere il ciclo. Calcolare:
(a) la massima T del ciclo;
(b) il lavoro fatto nel ciclo;
(c) il calore scambiato.



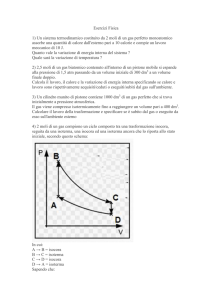

![1] Partendo dallo stato iniziale A (PA = 1 atm, V = 1 l ), un gas](http://s1.studylibit.com/store/data/005904298_1-61e24a21bd4c05eedb266c215e76813f-300x300.png)






